62 Variable Transformations
62.1 Rationale
In order to obtain reliable model fits and inference on linear models, the model assumptions described earlier must be satisfied.
Sometimes it is necessary to transform the response variable and/or some of the explanatory variables.
This process should involve data visualization and exploration.
62.2 Power and Log Transformations
It is often useful to explore power and log transforms of the variables, e.g., \(\log(y)\) or \(y^\lambda\) for some \(\lambda\) (and likewise \(\log(x)\) or \(x^\lambda\)).
You can read more about the Box-Cox family of power transformations.
62.3 Diamonds Data
> data("diamonds", package="ggplot2")
> head(diamonds)
# A tibble: 6 x 10
carat cut color clarity depth table price x y z
<dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl>
1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
4 0.290 Premium I VS2 62.4 58 334 4.2 4.23 2.63
5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.4862.4 Nonlinear Relationship
> ggplot(data = diamonds) +
+ geom_point(mapping=aes(x=carat, y=price, color=clarity), alpha=0.3)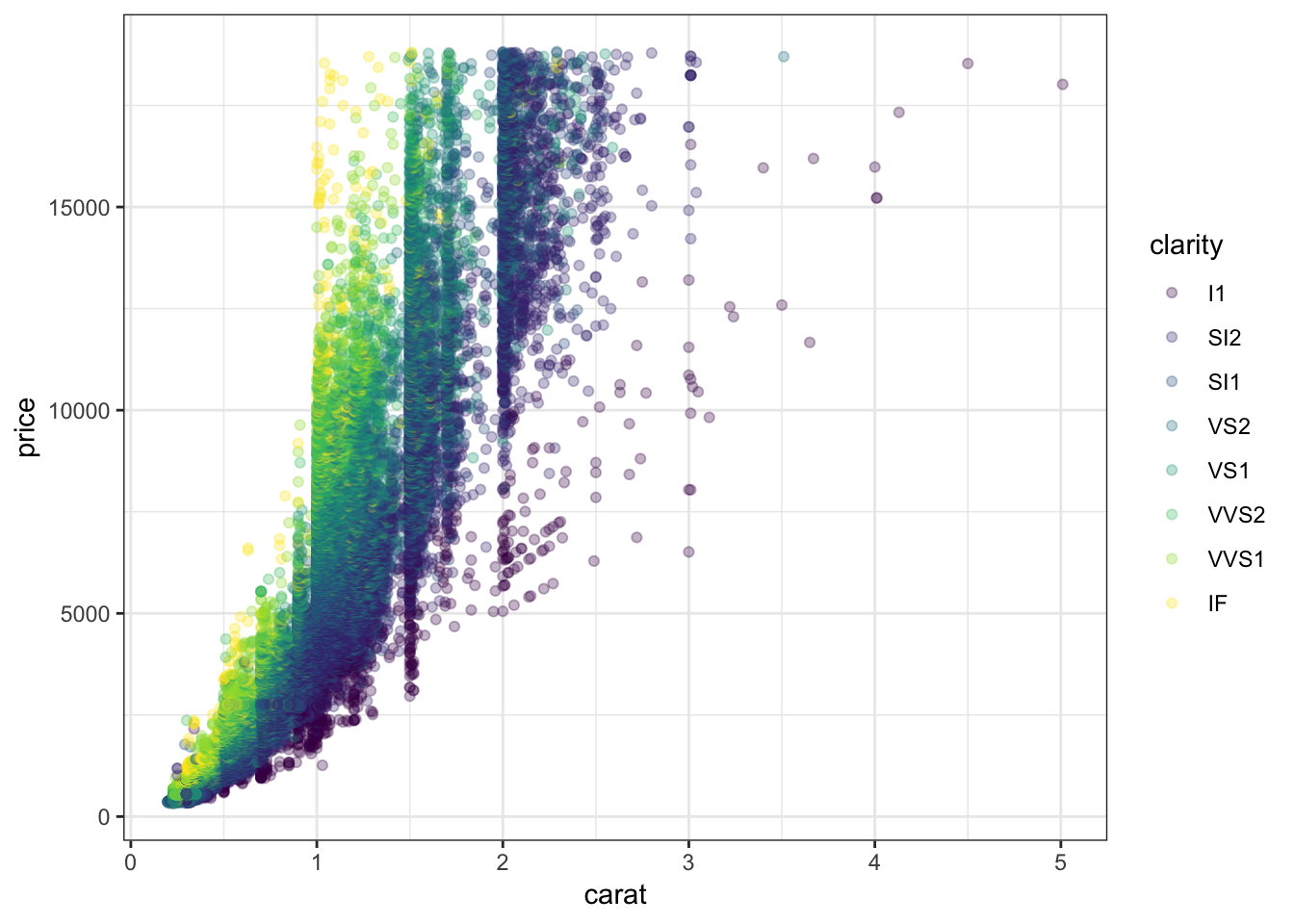
62.5 Regression with Nonlinear Relationship
> diam_fit <- lm(price ~ carat + clarity, data=diamonds)
> anova(diam_fit)
Analysis of Variance Table
Response: price
Df Sum Sq Mean Sq F value Pr(>F)
carat 1 7.2913e+11 7.2913e+11 435639.9 < 2.2e-16 ***
clarity 7 3.9082e+10 5.5831e+09 3335.8 < 2.2e-16 ***
Residuals 53931 9.0264e+10 1.6737e+06
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 162.6 Residual Distribution
> plot(diam_fit, which=1)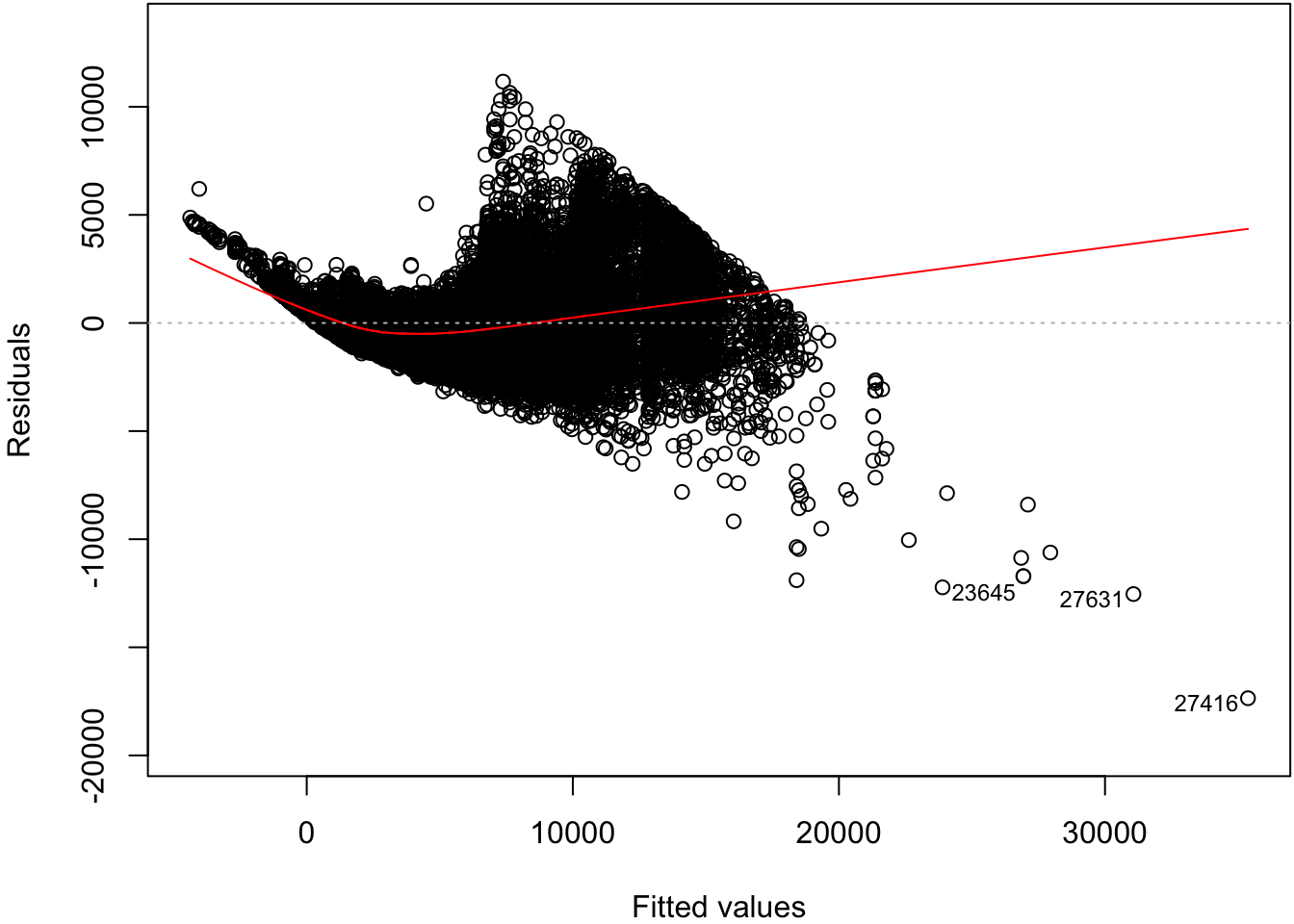
62.7 Normal Residuals Check
> plot(diam_fit, which=2)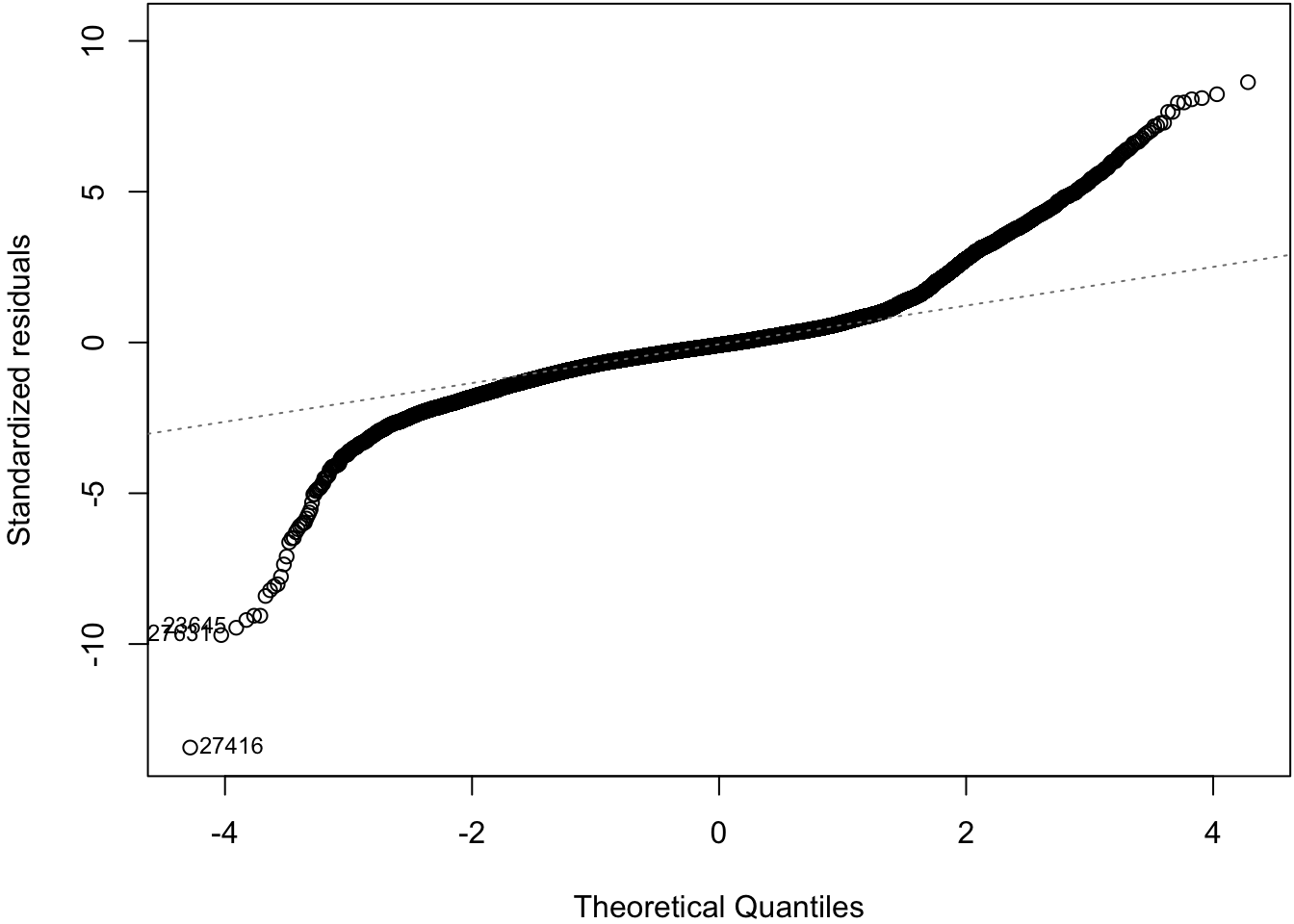
62.8 Log-Transformation
> ggplot(data = diamonds) +
+ geom_point(aes(x=carat, y=price, color=clarity), alpha=0.3) +
+ scale_y_log10(breaks=c(1000,5000,10000)) +
+ scale_x_log10(breaks=1:5)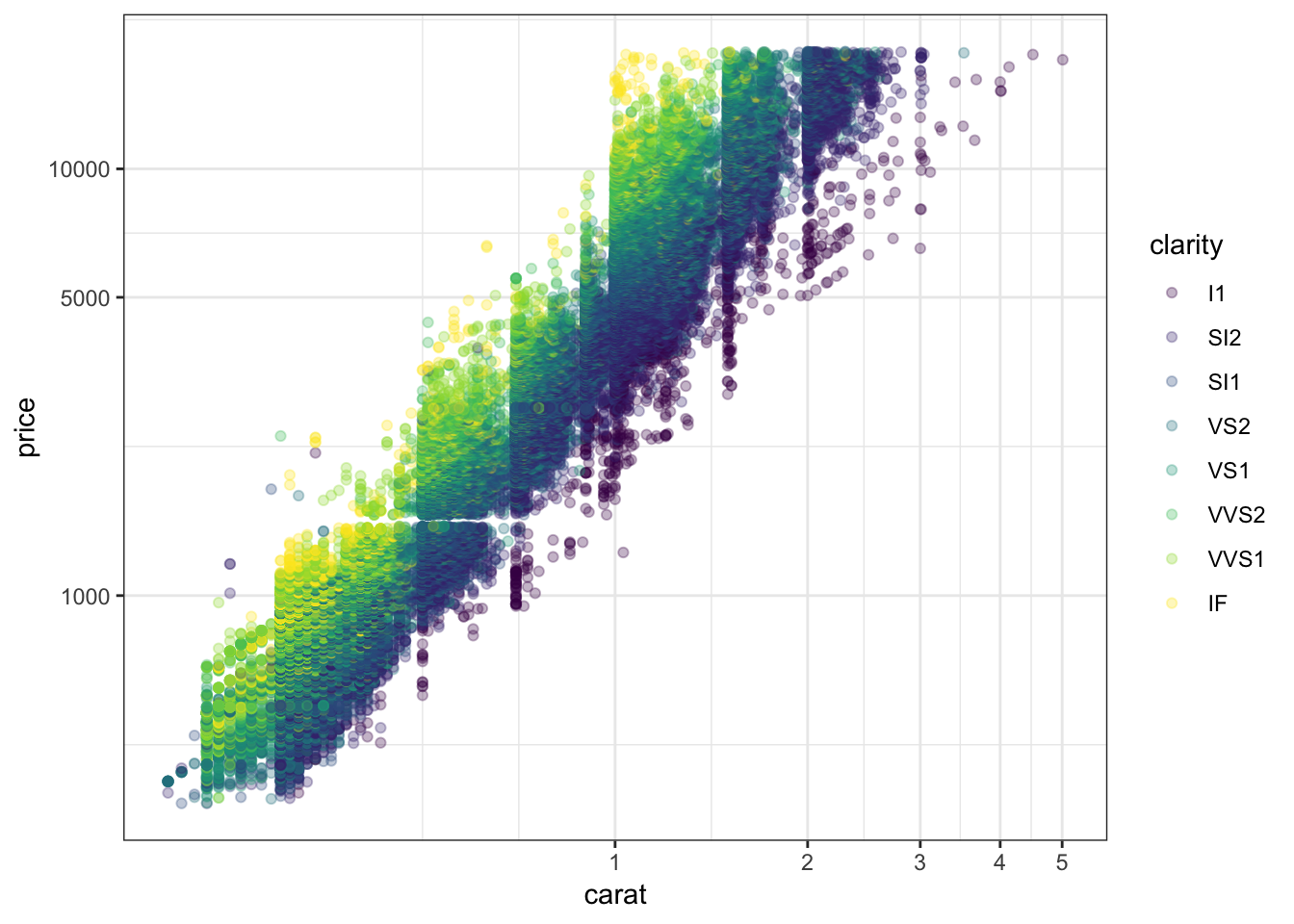
62.9 OLS on Log-Transformed Data
> diamonds <- mutate(diamonds, log_price = log(price, base=10),
+ log_carat = log(carat, base=10))
> ldiam_fit <- lm(log_price ~ log_carat + clarity, data=diamonds)
> anova(ldiam_fit)
Analysis of Variance Table
Response: log_price
Df Sum Sq Mean Sq F value Pr(>F)
log_carat 1 9771.9 9771.9 1452922.6 < 2.2e-16 ***
clarity 7 339.1 48.4 7203.3 < 2.2e-16 ***
Residuals 53931 362.7 0.0
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 162.10 Residual Distribution
> plot(ldiam_fit, which=1)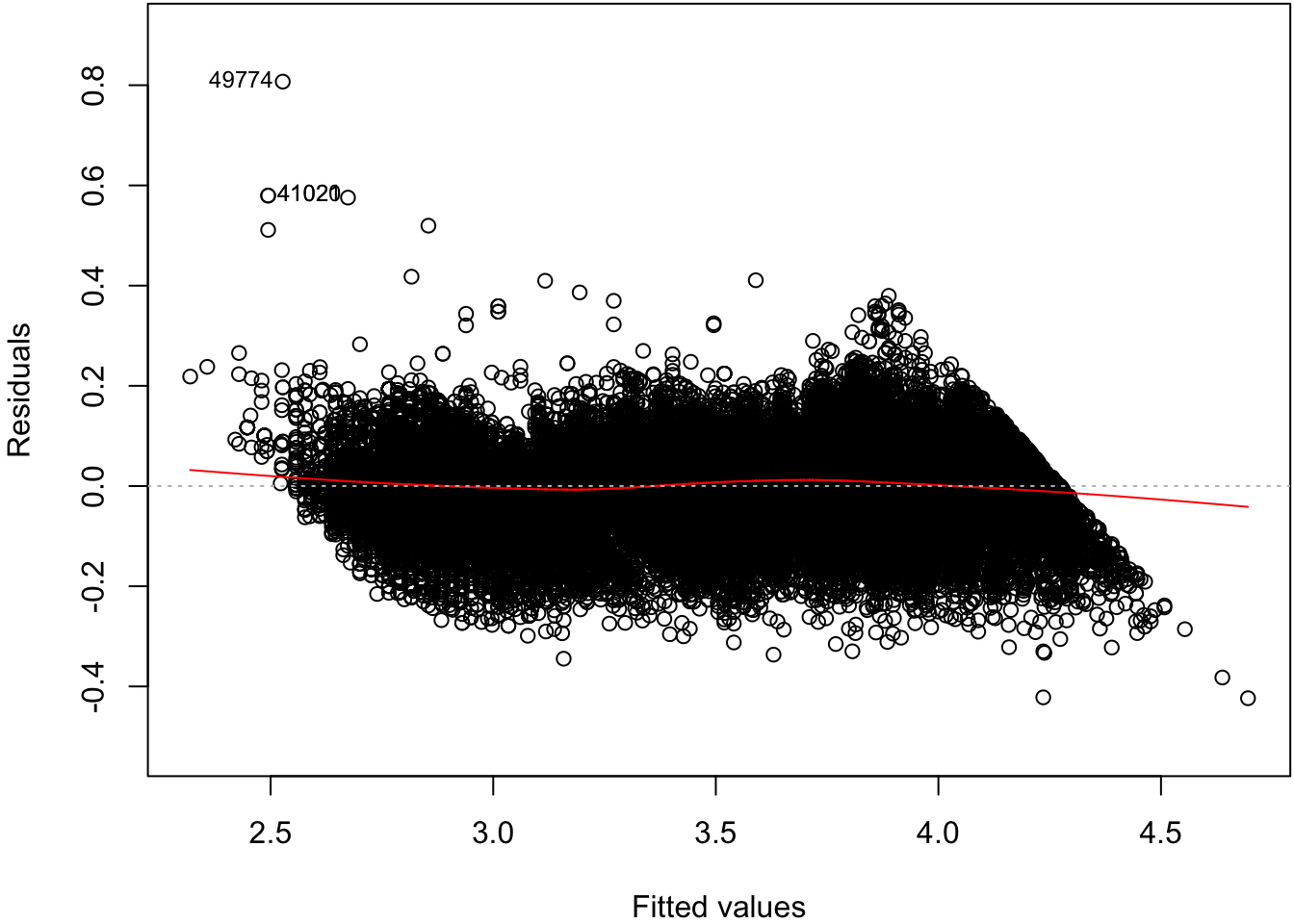
62.11 Normal Residuals Check
> plot(ldiam_fit, which=2)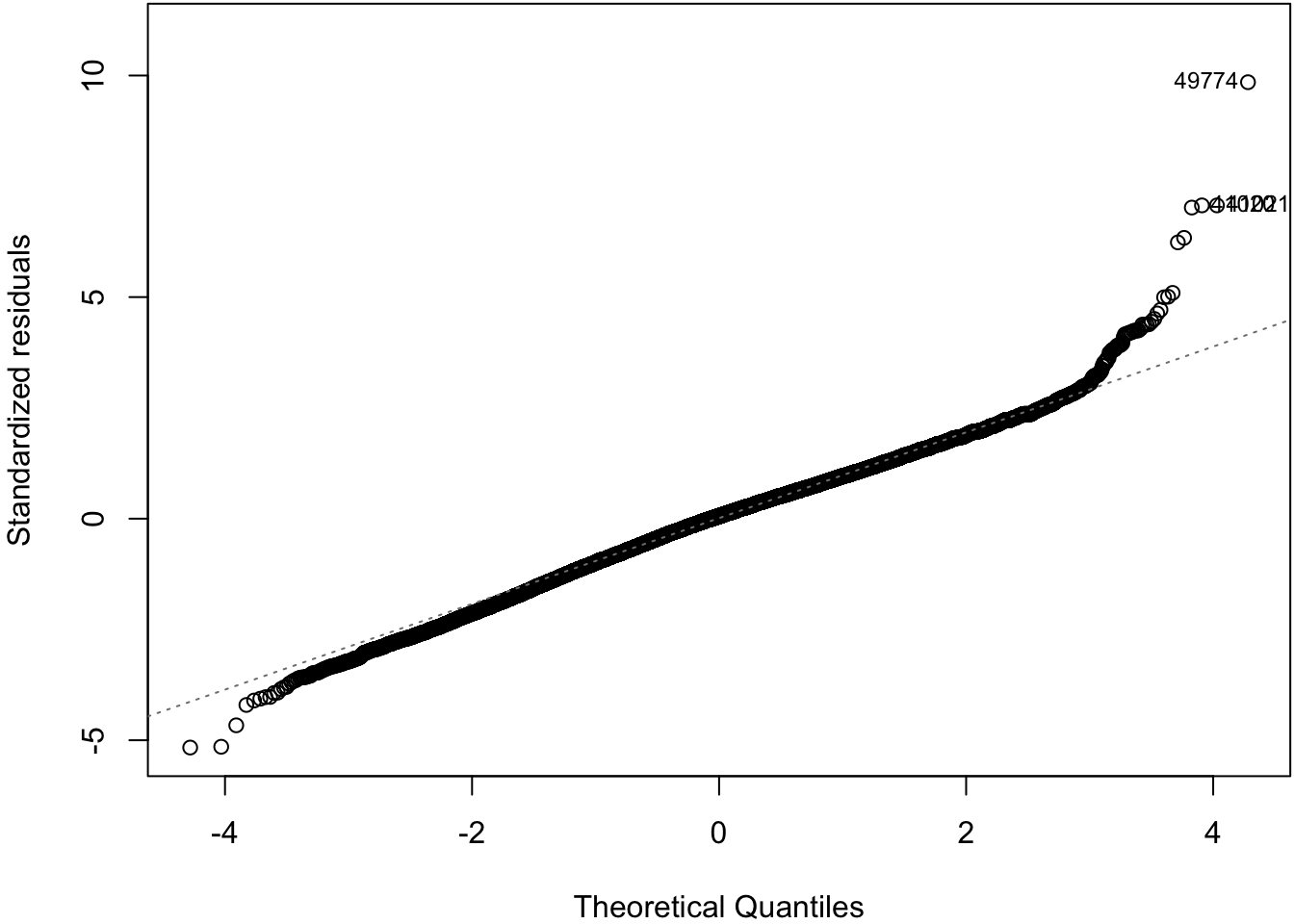
62.12 Tree Pollen Study
Suppose that we have a study where tree pollen measurements are averaged every week, and these data are recorded for 10 years. These data are simulated:
> pollen_study
# A tibble: 520 x 3
week year pollen
<int> <int> <dbl>
1 1 2001 1842.
2 2 2001 1966.
3 3 2001 2381.
4 4 2001 2141.
5 5 2001 2210.
6 6 2001 2585.
7 7 2001 2392.
8 8 2001 2105.
9 9 2001 2278.
10 10 2001 2384.
# … with 510 more rows62.13 Tree Pollen Count by Week
> ggplot(pollen_study) + geom_point(aes(x=week, y=pollen))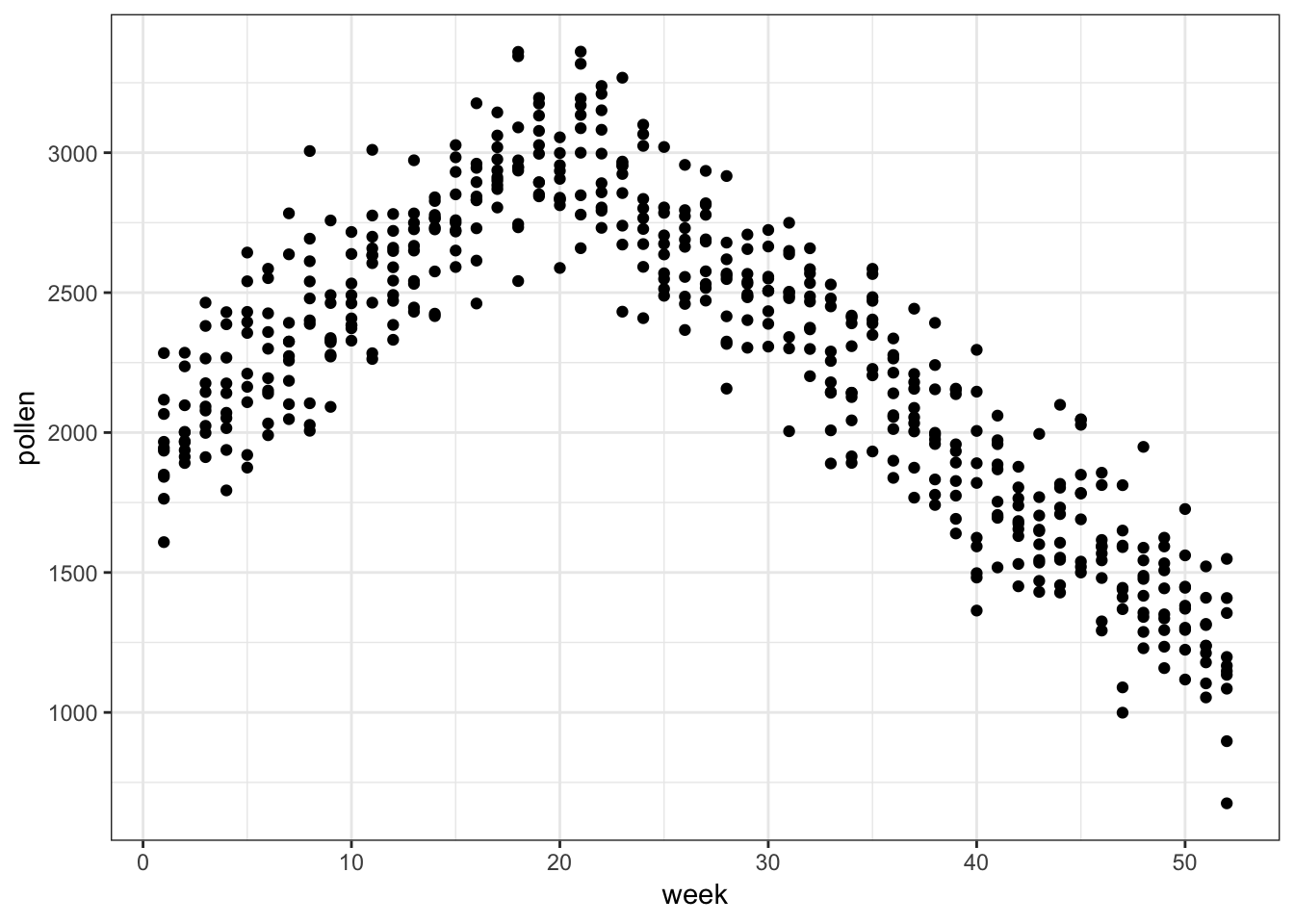
62.14 A Clever Transformation
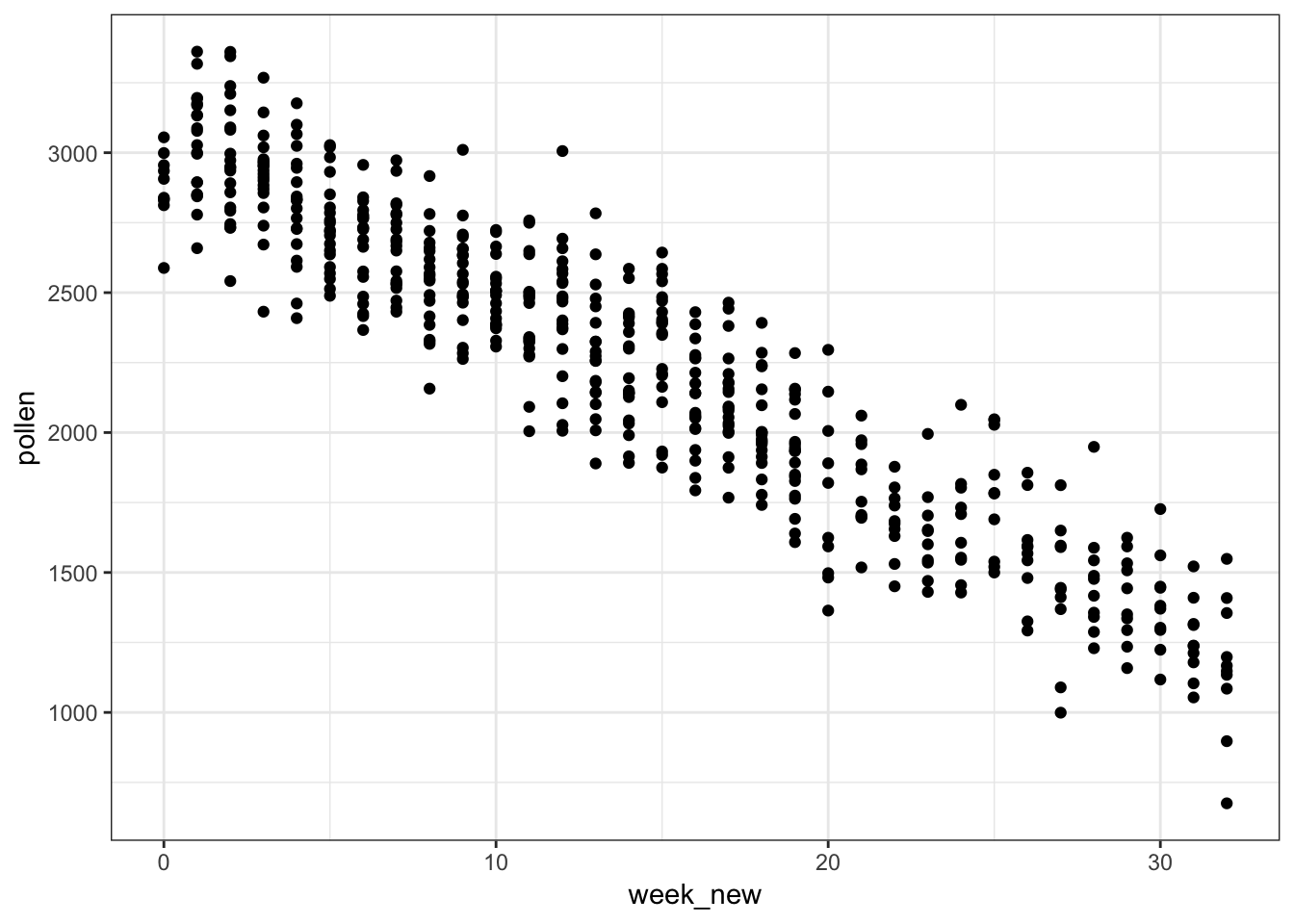
We can see there is a linear relationship between pollen and week if we transform week to be number of weeks from the peak week.
> pollen_study <- pollen_study %>%
+ mutate(week_new = abs(week-20))Note that this is a very different transformation from taking a log or power transformation.
62.15 week Transformed
> ggplot(pollen_study) + geom_point(aes(x=week_new, y=pollen))