32 Likelihood Function

32.1 Same MLE, Different \(L(\theta | \boldsymbol{x})\)

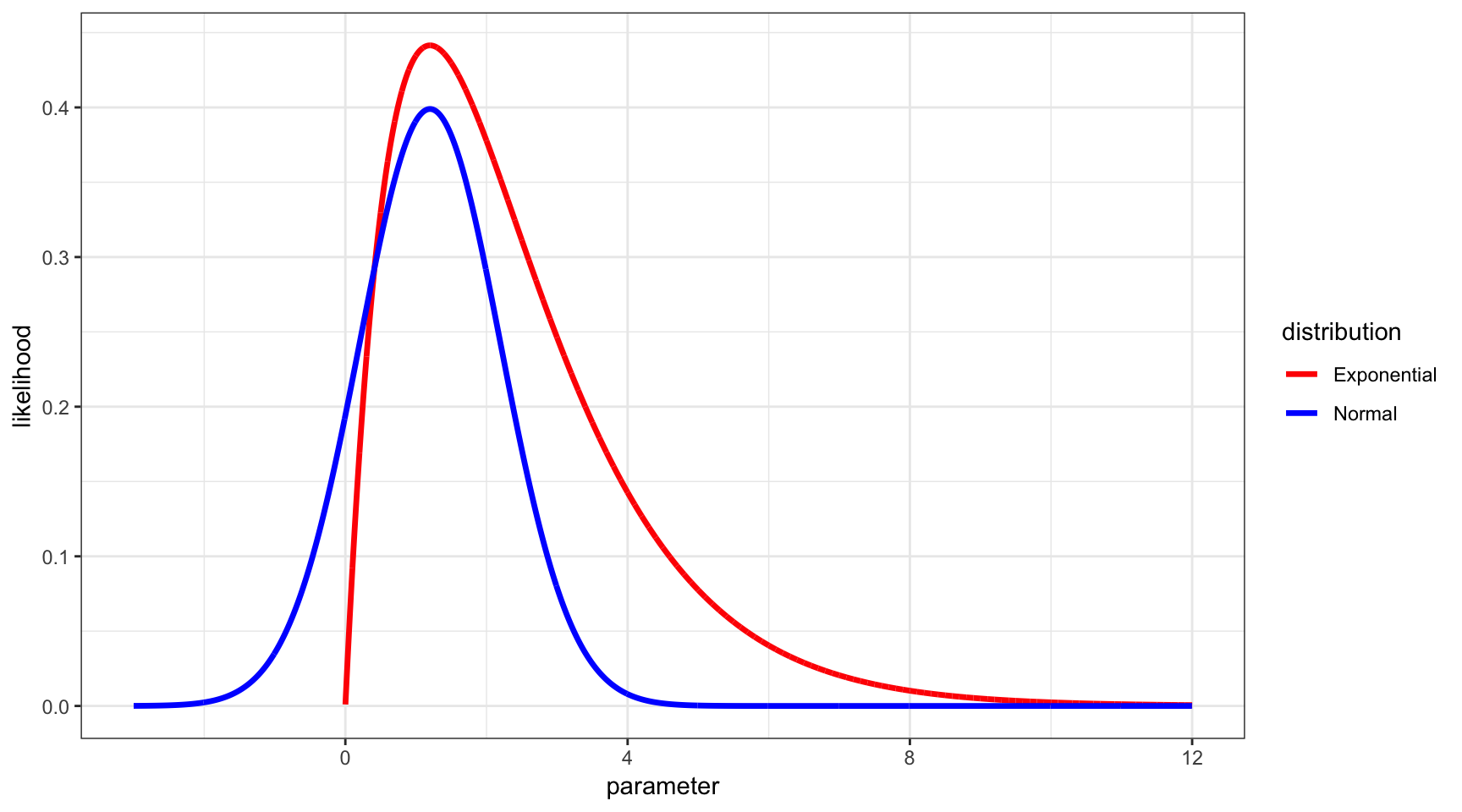
32.2 Weighted Likelihood Estimate

Instead of employing estimator \(\hat{\theta}_{{\rm MLE}} = \operatorname{argmax}_\theta L(\theta ; \boldsymbol{x})\), consider instead an arbitrary weight function, \(g(\theta)\). We could take a weighted average of the likelihood function, assuming all of the integrals below exist.

\[ \tilde{\theta} = \frac{\int \theta g(\theta) L(\theta ; \boldsymbol{x}) d\theta}{\int g(\theta) L(\theta ; \boldsymbol{x}) d\theta} \]

32.3 Conditional Expected Value

If we set

\[ h(\theta | \boldsymbol{x}) = \frac{g(\theta) L(\theta ; \boldsymbol{x})}{\int g(\theta^*) L(\theta^* ; \boldsymbol{x}) d\theta^*} \]

then \(h(\theta | \boldsymbol{x})\) is a probability density function and

\[ \tilde{\theta} = {\operatorname{E}}_{h(\theta | \boldsymbol{x})}[\theta]. \]

32.4 Standard Errror

Consider the model, \(X_1, X_2, \ldots, X_n {\; \stackrel{\text{iid}}{\sim}\;}F_{\theta}\).

Since \(\tilde{\theta} = {\operatorname{E}}_{h(\theta | \boldsymbol{x})}[\theta]\) is a function of the data \(\boldsymbol{x}\), it follows that in most circumstances it should be possible to obtain an approximation to its standard error, \(\sqrt{{\operatorname{Var}}(\tilde{\theta})}\) and an estimate of the standard error.

This allows for frequentist inference of estimates based on a weighted integral of the likelihood function.