13 Discrete RVs
13.1 Uniform (Discrete)
This simple rv distribution assigns equal probabilities to a finite set of values:
\[X \sim \mbox{Uniform}\{1, 2, \ldots, n\}\]
\[\mathcal{R} = \{1, 2, \ldots, n\}\]
\[f(x; n) = 1/n \mbox{ for } x \in \mathcal{R}\]
\[{\operatorname{E}}[X] = \frac{n+1}{2}, \ {\operatorname{Var}}(X) = \frac{n^2-1}{12}\]
13.2 Uniform (Discrete) PMF
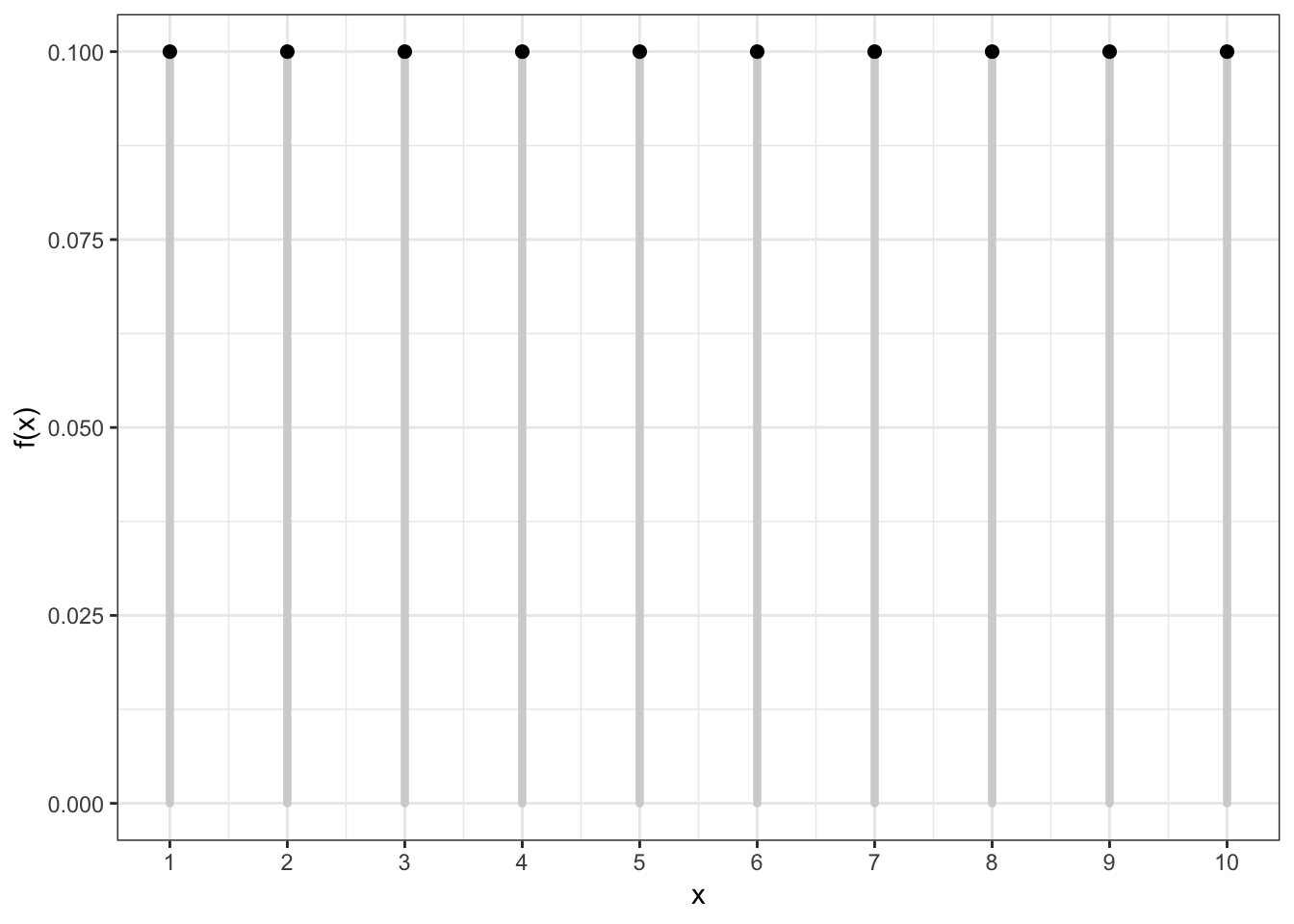
13.3 Uniform (Discrete) in R
There is no family of functions built into R for this distribution since it is so simple. However, it is possible to generate random values via the sample function:
> n <- 20L
> sample(x=1:n, size=10, replace=TRUE)
[1] 9 15 6 8 13 19 19 1 20 14
>
> x <- sample(x=1:n, size=1e6, replace=TRUE)
> mean(x) - (n+1)/2
[1] -0.007369
> var(x) - (n^2-1)/12
[1] 0.0242949713.4 Bernoulli
A single success/failure event, such as heads/tails when flipping a coin or survival/death.
\[X \sim \mbox{Bernoulli}(p)\]
\[\mathcal{R} = \{0, 1\}\]
\[f(x; p) = p^x (1-p)^{1-x} \mbox{ for } x \in \mathcal{R}\]
\[{\operatorname{E}}[X] = p, \ {\operatorname{Var}}(X) = p(1-p)\]
13.5 Binomial
An extension of the Bernoulli distribution to simultaneously considering \(n\) independent success/failure trials and counting the number of successes.
\[X \sim \mbox{Binomial}(n, p)\]
\[\mathcal{R} = \{0, 1, 2, \ldots, n\}\]
\[f(x; p) = {n \choose x} p^x (1-p)^{n-x} \mbox{ for } x \in \mathcal{R}\]
\[{\operatorname{E}}[X] = np, \ {\operatorname{Var}}(X) = np(1-p)\]
Note that \({n \choose x} = \frac{n!}{x! (n-x)!}\) is the number of unique ways to choose \(x\) items from \(n\) without respect to order.
13.6 Binomial PMF
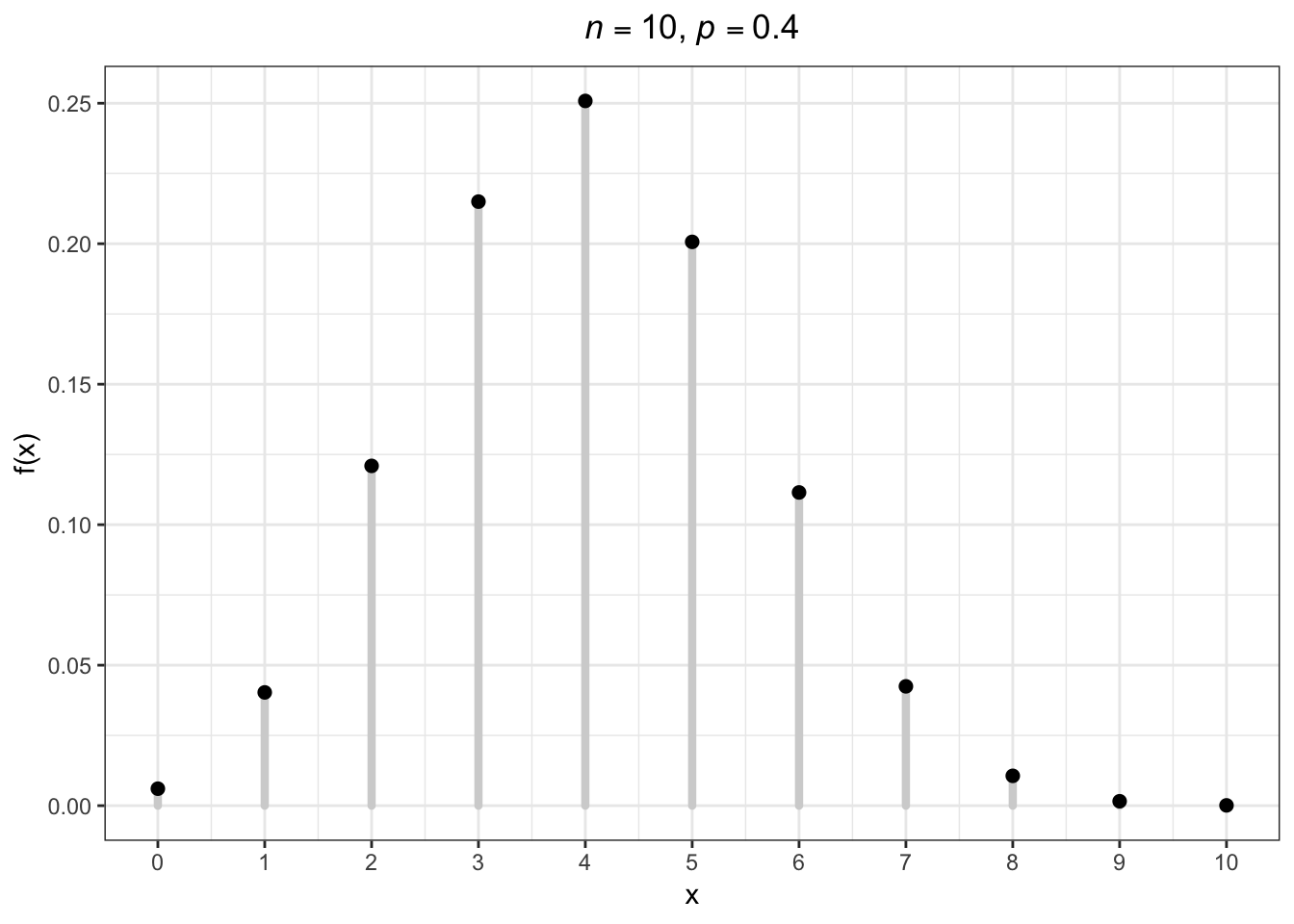
13.7 Binomial in R
> str(dbinom)
function (x, size, prob, log = FALSE) > str(pbinom)
function (q, size, prob, lower.tail = TRUE, log.p = FALSE) > str(qbinom)
function (p, size, prob, lower.tail = TRUE, log.p = FALSE) > str(rbinom)
function (n, size, prob) 13.8 Poisson
Models the number of occurrences of something within a defined time/space period, where the occurrences are independent. Examples: the number of lightning strikes on campus in a given year; the number of emails received on a given day.
\[X \sim \mbox{Poisson}(\lambda)\]
\[\mathcal{R} = \{0, 1, 2, 3, \ldots \}\]
\[f(x; \lambda) = \frac{\lambda^x e^{-\lambda}}{x!} \mbox{ for } x \in \mathcal{R}\]
\[{\operatorname{E}}[X] = \lambda, \ {\operatorname{Var}}(X) = \lambda\]
13.9 Poisson PMF
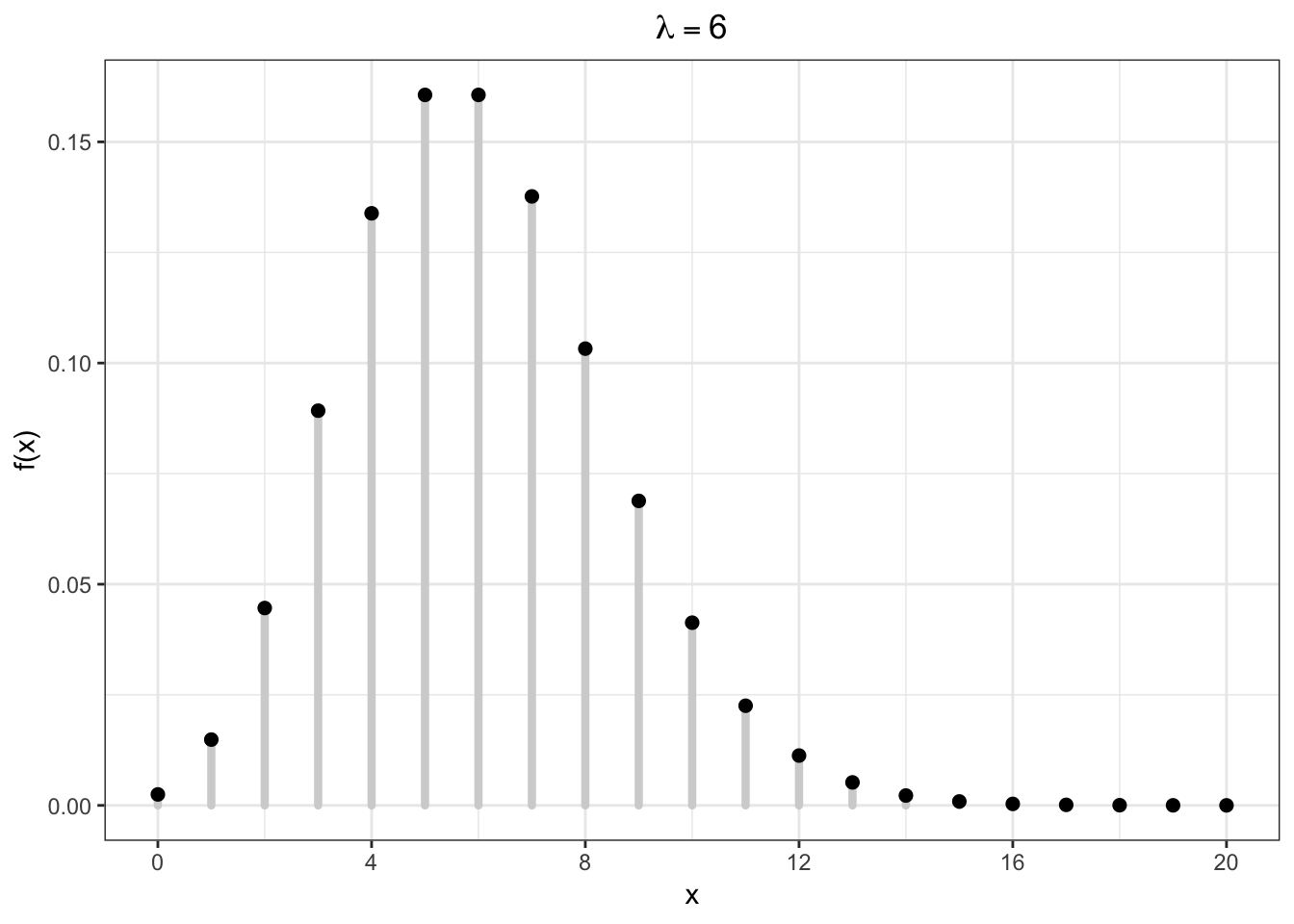
13.10 Poisson in R
> str(dpois)
function (x, lambda, log = FALSE) > str(ppois)
function (q, lambda, lower.tail = TRUE, log.p = FALSE) > str(qpois)
function (p, lambda, lower.tail = TRUE, log.p = FALSE) > str(rpois)
function (n, lambda)