60 OLS in R
R implements OLS of multiple explanatory variables exactly the same as with a single explanatory variable, except we need to show the sum of all explanatory variables that we want to use.
> lm(weight ~ height + sex, data=htwt)
Call:
lm(formula = weight ~ height + sex, data = htwt)
Coefficients:
(Intercept) height sexM
-76.6167 0.8106 8.2269 60.1 Weight Regressed on Height + Sex
> summary(lm(weight ~ height + sex, data=htwt))
Call:
lm(formula = weight ~ height + sex, data = htwt)
Residuals:
Min 1Q Median 3Q Max
-20.131 -4.884 -0.640 5.160 41.490
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -76.6167 15.7150 -4.875 2.23e-06 ***
height 0.8105 0.0953 8.506 4.50e-15 ***
sexM 8.2269 1.7105 4.810 3.00e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 8.066 on 197 degrees of freedom
Multiple R-squared: 0.6372, Adjusted R-squared: 0.6335
F-statistic: 173 on 2 and 197 DF, p-value: < 2.2e-1660.2 One Variable, Two Scales
We can include a single variable but on two different scales:
> htwt <- htwt %>% mutate(height2 = height^2)
> summary(lm(weight ~ height + height2, data=htwt))
Call:
lm(formula = weight ~ height + height2, data = htwt)
Residuals:
Min 1Q Median 3Q Max
-24.265 -5.159 -0.499 4.549 42.965
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 107.117140 175.246872 0.611 0.542
height -1.632719 2.045524 -0.798 0.426
height2 0.008111 0.005959 1.361 0.175
Residual standard error: 8.486 on 197 degrees of freedom
Multiple R-squared: 0.5983, Adjusted R-squared: 0.5943
F-statistic: 146.7 on 2 and 197 DF, p-value: < 2.2e-1660.3 Interactions
It is possible to include products of explanatory variables, which is called an interaction.
> summary(lm(weight ~ height + sex + height:sex, data=htwt))
Call:
lm(formula = weight ~ height + sex + height:sex, data = htwt)
Residuals:
Min 1Q Median 3Q Max
-20.869 -4.835 -0.897 4.429 41.122
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -45.6730 22.1342 -2.063 0.0404 *
height 0.6227 0.1343 4.637 6.46e-06 ***
sexM -55.6571 32.4597 -1.715 0.0880 .
height:sexM 0.3729 0.1892 1.971 0.0502 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 8.007 on 196 degrees of freedom
Multiple R-squared: 0.6442, Adjusted R-squared: 0.6388
F-statistic: 118.3 on 3 and 196 DF, p-value: < 2.2e-1660.4 More on Interactions
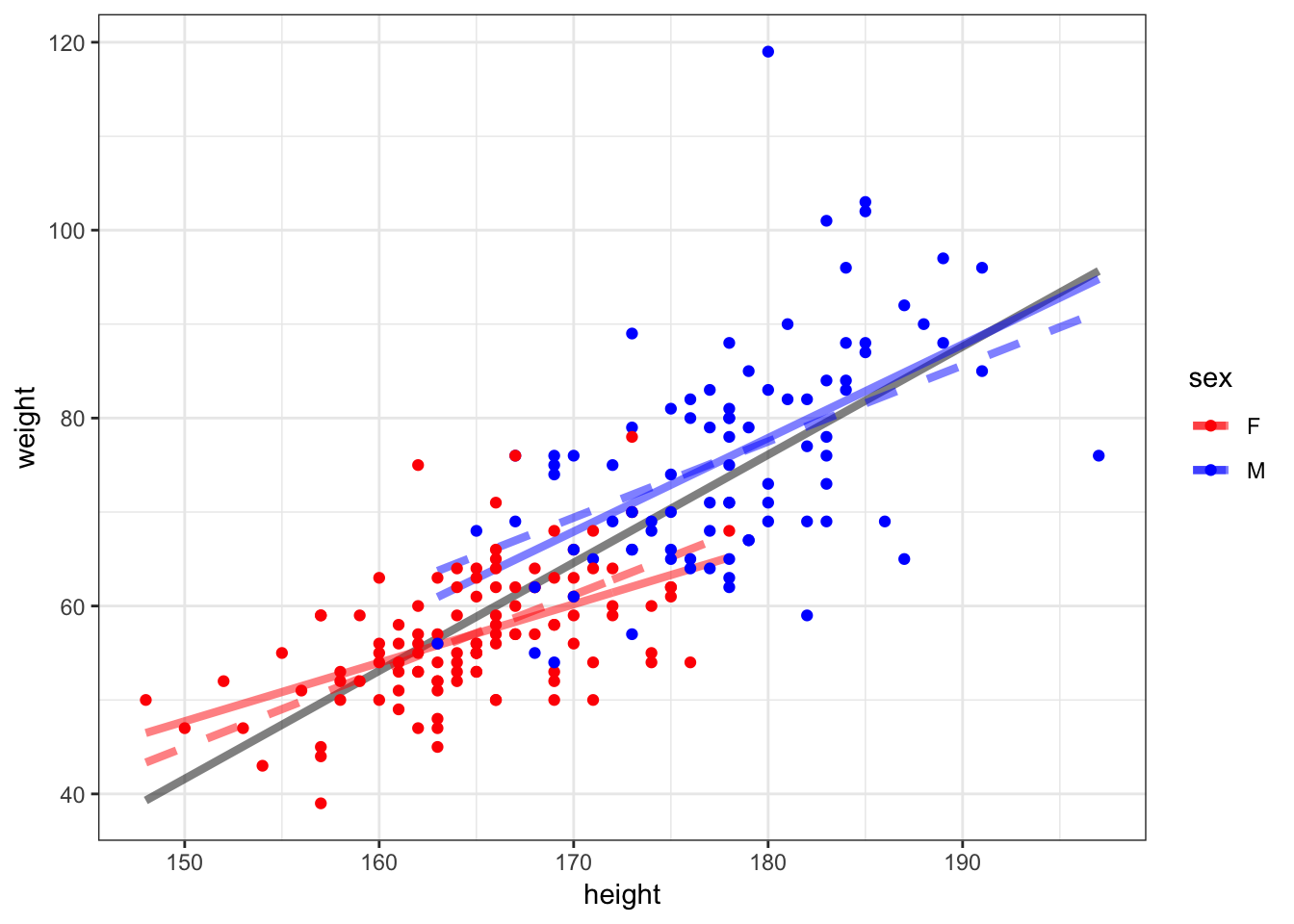
What happens when there is an interaction between a quantitative explanatory variable and a factor explanatory variable? In the next plot, we show three models:
- Grey solid:
lm(weight ~ height, data=htwt) - Color dashed:
lm(weight ~ height + sex, data=htwt) - Color solid:
lm(weight ~ height + sex + height:sex, data=htwt)
60.5 Visualizing Three Different Models