29 The t Distribution

29.1 Normal, Unknown Variance

Suppose a sample of $n$ data points is modeled by $X_1, X_2, \ldots, X_n \stackrel{{\rm iid}}{\sim} \mbox{Normal}(\mu, \sigma^2)$ where $\sigma^2$ is unknown. Recall that $S = \sqrt{\frac{\sum_{i=1}^n (X_i - \overline{X})^2}{n-1}}$ is the sample standard deviation.

The statistic $$\frac{\overline{X} - \mu}{S/\sqrt{n}}$$

has a $t_{n-1}$ distribution, a t-distribution with $n-1$ degrees of freedom.

29.2 Aside: Chi-Square Distribution

Suppose $Z_1, Z_2, \ldots, Z_v \stackrel{{\rm iid}}{\sim} \mbox{Normal}(0, 1)$. Then $Z_1^2 + Z_2^2 + \cdots + Z_v^2$ has a $\chi^2_v$ distribution, where $v$ is the degrees of freedom.

This $\chi^2_v$ rv has a pdf, expected value equal to $v$, and variance equal to $2v$.

Also,

$$\frac{(n-1) S^2}{\sigma^2} \sim \chi^2_{n-1}.$$

29.3 Theoretical Basis of the t

Suppose that $Z \sim \mbox{Normal}(0,1)$, $X \sim \chi^2_v$, and $Z$ and $X$ are independent. Then $\frac{Z}{\sqrt{X/v}}$ has a $t_v$ distribution.

Since $\frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \sim \mbox{Normal}(0,1)$ and $\overline{X}$ and $S^2$ are independent (shown later), it follows that the following has a $t_{n-1}$ distribution:

$$\frac{\overline{X} - \mu}{S/\sqrt{n}}.$$

29.4 When Is t Utilized?

• The t distribution and its corresponding CI’s and HT’s are utilized when the data are Normal (or approximately Normal) and $n$ is small
  
• Small typically means that $n < 30$
  
• In this case the inference based on the t distribution will be more accurate
• When $n \geq 30$, there is very little difference between using $t$-statistics and $z$-statistics

29.5 t vs Normal

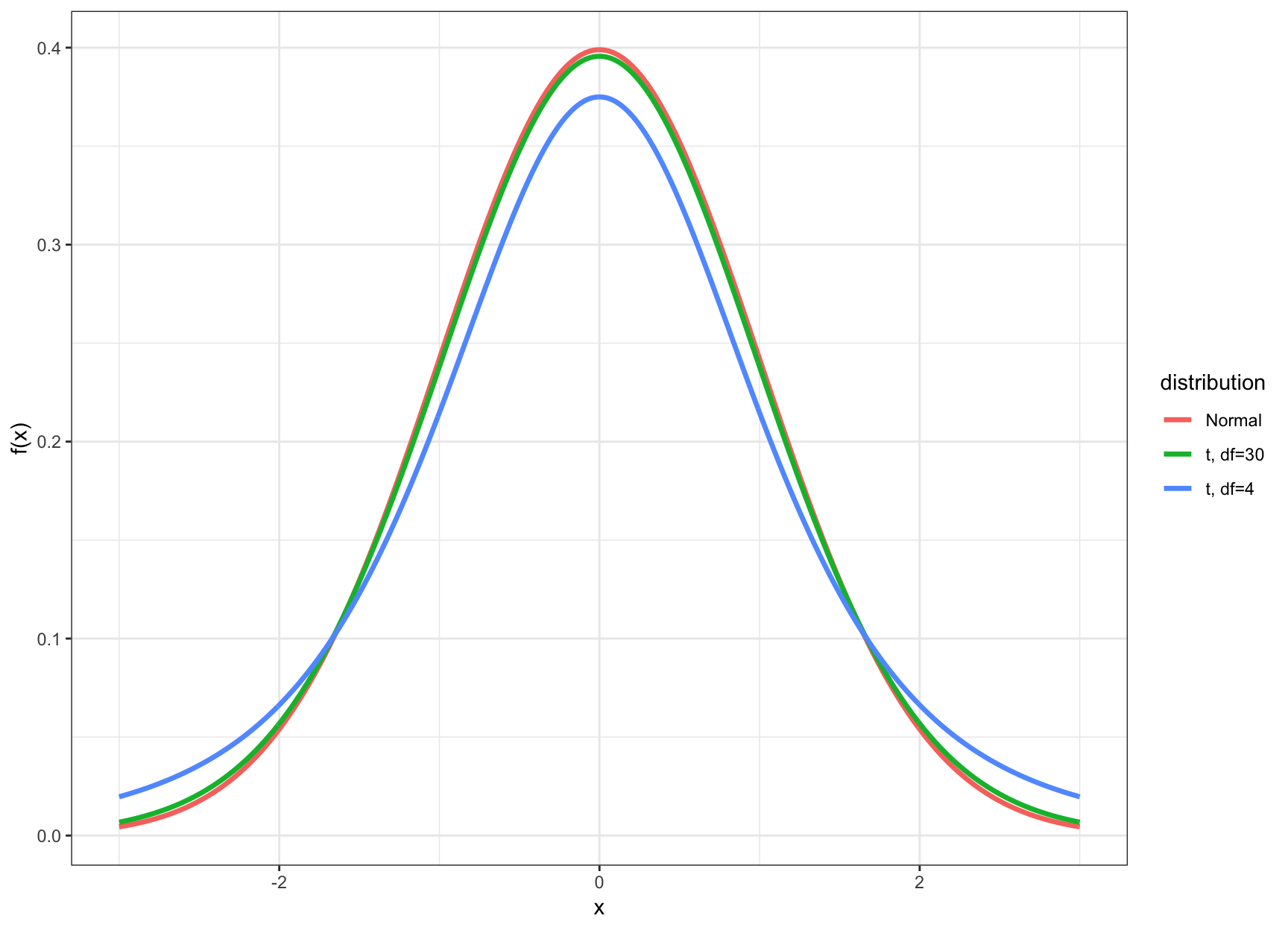
29.6 t Percentiles

We calculated percentiles of the Normal(0,1) distribution (e.g., $z_\alpha$). We can do the analogous calculation with the t distribution.

Let $t_\alpha$ be the $\alpha$ percentile of the t distribution. Examples:

> qt(0.025, df=4) # alpha = 0.025
[1] -2.776445
> qt(0.05, df=4)
[1] -2.131847
> qt(0.95, df=4)
[1] 2.131847
> qt(0.975, df=4)
[1] 2.776445

29.7 Confidence Intervals

Here is a $(1-\alpha)$-level CI for $\mu$ using this distribution:

$$\left(\hat{\mu} - |t_{\alpha/2}| \frac{s}{\sqrt{n}}, \hat{\mu} + |t_{\alpha/2}| \frac{s}{\sqrt{n}} \right),$$

where as before $\hat{\mu} = \overline{x}$. This produces a wider CI than the $z$ statistic analogue.

29.8 Hypothesis Tests

Suppose we want to test $H_0: \mu = \mu_0$ vs $H_1: \mu \not= \mu_0$ where $\mu_0$ is a known, given number.

The t-statistic is

$$t = \frac{\hat{\mu} - \mu_0}{\frac{s}{\sqrt{n}}}$$

with p-value

$${\rm Pr}(|T^*| \geq |t|)$$

where $T^* \sim t_{n-1}$.

29.9 Two-Sample t-Distribution

Let $X_1, X_2, \ldots, X_{n_1} \stackrel{{\rm iid}}{\sim} \mbox{Normal}(\mu_1, \sigma^2_1)$ and $Y_1, Y_2, \ldots, Y_{n_2} \stackrel{{\rm iid}}{\sim} \mbox{Normal}(\mu_2, \sigma^2_2)$ have unequal variances.

We have $\hat{\mu}_1 = \overline{X}$ and $\hat{\mu}_2 = \overline{Y}$. The unequal variance two-sample t-statistic is $$t = \frac{\hat{\mu}_1 - \hat{\mu}_2 - (\mu_1 - \mu_2)}{\sqrt{\frac{S^2_1}{n_1} + \frac{S^2_2}{n_2}}}.$$

29.10 Two-Sample t-Distribution

Let $X_1, X_2, \ldots, X_{n_1} \stackrel{{\rm iid}}{\sim} \mbox{Normal}(\mu_1, \sigma^2)$ and $Y_1, Y_2, \ldots, Y_{n_2} \stackrel{{\rm iid}}{\sim} \mbox{Normal}(\mu_2, \sigma^2)$ have equal variance.

We have $\hat{\mu}_1 = \overline{X}$ and $\hat{\mu}_2 = \overline{Y}$. The equal variance two-sample t-statistic is

$$t = \frac{\hat{\mu}_1 - \hat{\mu}_2 - (\mu_1 - \mu_2)}{\sqrt{\frac{S^2}{n_1} + \frac{S^2}{n_2}}}.$$

where

$$S^2 = \frac{\sum_{i=1}^{n_1}(X_i - \overline{X})^2 + \sum_{i=1}^{n_2}(Y_i - \overline{Y})^2}{n_1 + n_2 - 2}.$$

29.11 Two-Sample t-Distributions

When the two populations have equal variances, the pivotal t-statistic follows a $t_{n_1 + n_2 -2}$ distribution.

When there are unequal variances, the pivotal t-statistic follows a t distribution where the degrees of freedom comes from an approximation using the Welch–Satterthwaite equation (which R calculates).