61 Categorical Explanatory Variables
61.1 Example: Chicken Weights
> data("chickwts", package="datasets")
> head(chickwts)
weight feed
1 179 horsebean
2 160 horsebean
3 136 horsebean
4 227 horsebean
5 217 horsebean
6 168 horsebean
> summary(chickwts$feed)
casein horsebean linseed meatmeal soybean sunflower
12 10 12 11 14 12 61.2 Factor Variables in lm()
> chick_fit <- lm(weight ~ feed, data=chickwts)
> summary(chick_fit)
Call:
lm(formula = weight ~ feed, data = chickwts)
Residuals:
Min 1Q Median 3Q Max
-123.909 -34.413 1.571 38.170 103.091
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 323.583 15.834 20.436 < 2e-16 ***
feedhorsebean -163.383 23.485 -6.957 2.07e-09 ***
feedlinseed -104.833 22.393 -4.682 1.49e-05 ***
feedmeatmeal -46.674 22.896 -2.039 0.045567 *
feedsoybean -77.155 21.578 -3.576 0.000665 ***
feedsunflower 5.333 22.393 0.238 0.812495
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 54.85 on 65 degrees of freedom
Multiple R-squared: 0.5417, Adjusted R-squared: 0.5064
F-statistic: 15.36 on 5 and 65 DF, p-value: 5.936e-1061.3 Plot the Fit
> plot(chickwts$feed, chickwts$weight, xlab="Feed", ylab="Weight", las=2)
> points(chickwts$feed, chick_fit$fitted.values, col="blue", pch=20, cex=2)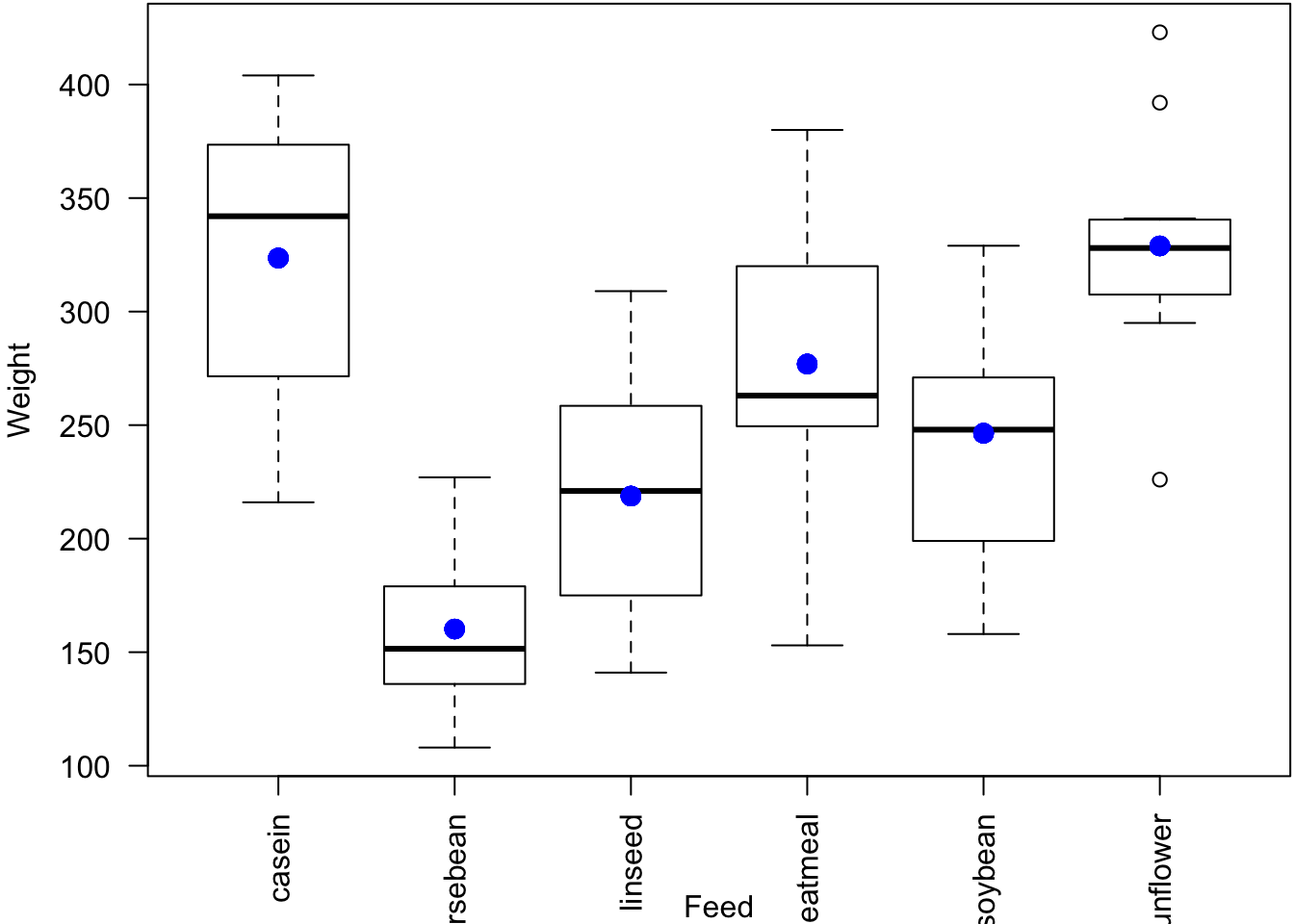
61.4 ANOVA (Version 1)
ANOVA (analysis of variance) was originally developed as a statistical model and method for comparing differences in mean values between various groups.
ANOVA quantifies and tests for differences in response variables with respect to factor variables.
In doing so, it also partitions the total variance to that due to within and between groups, where groups are defined by the factor variables.
61.5 anova()
The classic ANOVA table:
> anova(chick_fit)
Analysis of Variance Table
Response: weight
Df Sum Sq Mean Sq F value Pr(>F)
feed 5 231129 46226 15.365 5.936e-10 ***
Residuals 65 195556 3009
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1> n <- length(chick_fit$residuals) # n <- 71
> (n-1)*var(chick_fit$fitted.values)
[1] 231129.2
> (n-1)*var(chick_fit$residuals)
[1] 195556
> (n-1)*var(chickwts$weight) # sum of above two quantities
[1] 426685.2
> (231129/5)/(195556/65) # F-statistic
[1] 15.3647961.6 How It Works
> levels(chickwts$feed)
[1] "casein" "horsebean" "linseed" "meatmeal" "soybean" "sunflower"
> head(chickwts, n=3)
weight feed
1 179 horsebean
2 160 horsebean
3 136 horsebean
> tail(chickwts, n=3)
weight feed
69 222 casein
70 283 casein
71 332 casein
> x <- model.matrix(weight ~ feed, data=chickwts)
> dim(x)
[1] 71 661.7 Top of Design Matrix
> head(x)
(Intercept) feedhorsebean feedlinseed feedmeatmeal feedsoybean
1 1 1 0 0 0
2 1 1 0 0 0
3 1 1 0 0 0
4 1 1 0 0 0
5 1 1 0 0 0
6 1 1 0 0 0
feedsunflower
1 0
2 0
3 0
4 0
5 0
6 061.8 Bottom of Design Matrix
> tail(x)
(Intercept) feedhorsebean feedlinseed feedmeatmeal feedsoybean
66 1 0 0 0 0
67 1 0 0 0 0
68 1 0 0 0 0
69 1 0 0 0 0
70 1 0 0 0 0
71 1 0 0 0 0
feedsunflower
66 0
67 0
68 0
69 0
70 0
71 061.9 Model Fits
> chick_fit$fitted.values %>% round(digits=4) %>% unique()
[1] 160.2000 218.7500 246.4286 328.9167 276.9091 323.5833> chickwts %>% group_by(feed) %>% summarize(mean(weight))
# A tibble: 6 x 2
feed `mean(weight)`
<fct> <dbl>
1 casein 324.
2 horsebean 160.
3 linseed 219.
4 meatmeal 277.
5 soybean 246.
6 sunflower 329.