65 glm() Function in R
65.1 Example: Grad School Admissions
> mydata <-
+ read.csv("https://stats.idre.ucla.edu/stat/data/binary.csv")
> dim(mydata)
[1] 400 4
> head(mydata)
admit gre gpa rank
1 0 380 3.61 3
2 1 660 3.67 3
3 1 800 4.00 1
4 1 640 3.19 4
5 0 520 2.93 4
6 1 760 3.00 2Data and analysis courtesy of http://www.ats.ucla.edu/stat/r/dae/logit.htm.
65.2 Explore the Data
> apply(mydata, 2, mean)
admit gre gpa rank
0.3175 587.7000 3.3899 2.4850
> apply(mydata, 2, sd)
admit gre gpa rank
0.4660867 115.5165364 0.3805668 0.9444602
>
> table(mydata$admit, mydata$rank)
1 2 3 4
0 28 97 93 55
1 33 54 28 12> ggplot(data=mydata) +
+ geom_boxplot(aes(x=as.factor(admit), y=gre))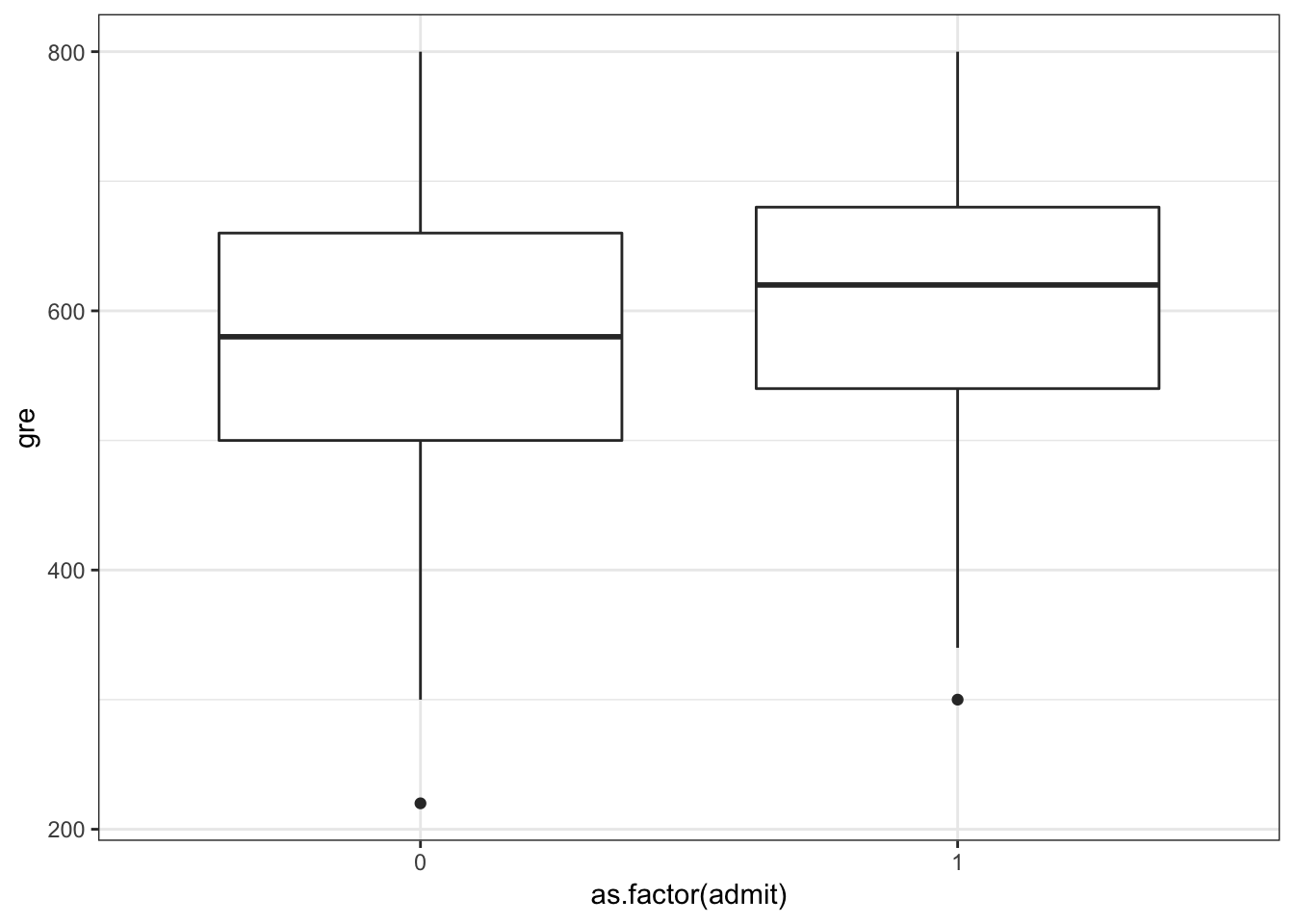
> ggplot(data=mydata) +
+ geom_boxplot(aes(x=as.factor(admit), y=gpa))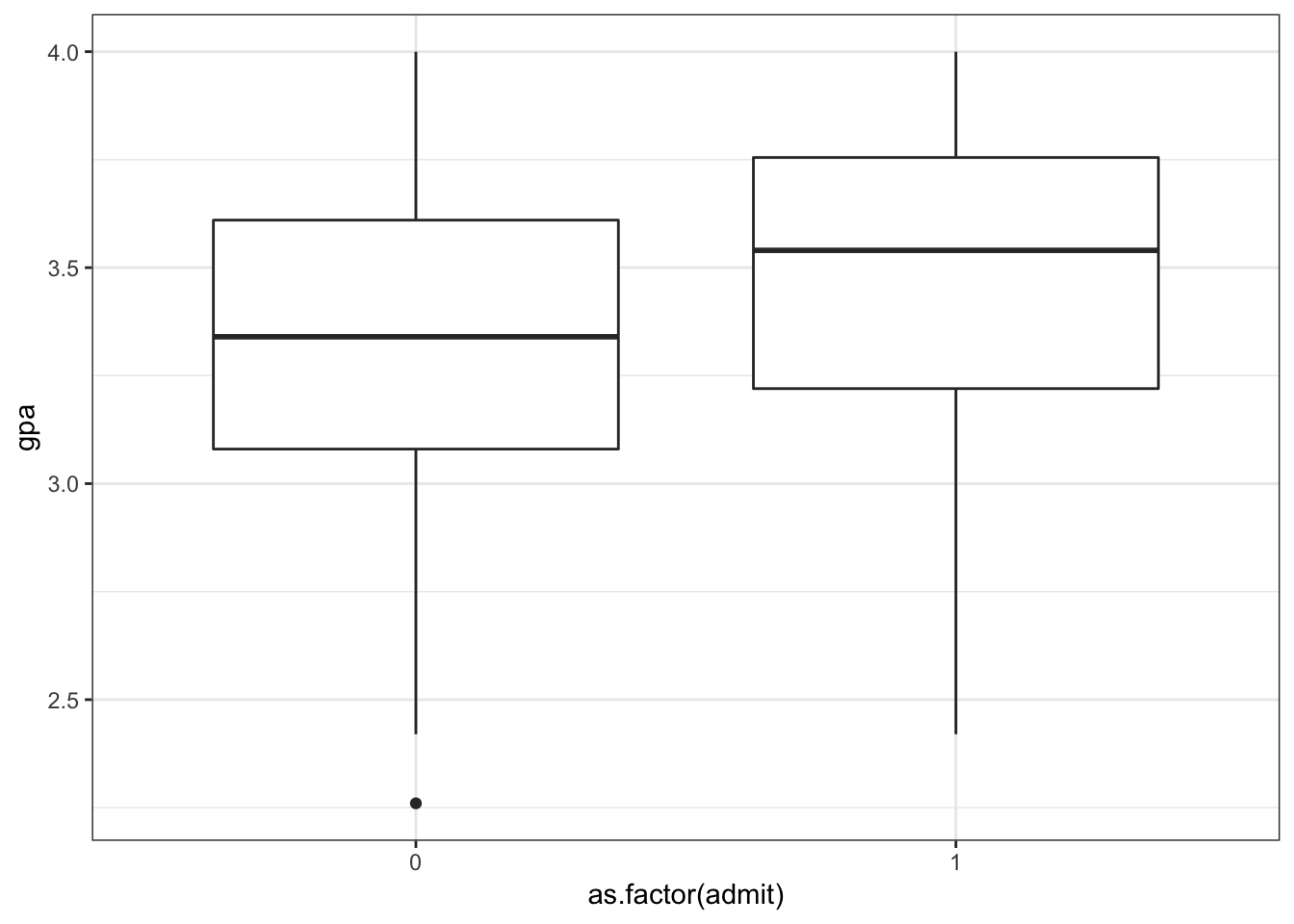
65.3 Logistic Regression in R
> mydata$rank <- factor(mydata$rank, levels=c(1, 2, 3, 4))
> myfit <- glm(admit ~ gre + gpa + rank,
+ data = mydata, family = "binomial")
> myfit
Call: glm(formula = admit ~ gre + gpa + rank, family = "binomial",
data = mydata)
Coefficients:
(Intercept) gre gpa rank2 rank3
-3.989979 0.002264 0.804038 -0.675443 -1.340204
rank4
-1.551464
Degrees of Freedom: 399 Total (i.e. Null); 394 Residual
Null Deviance: 500
Residual Deviance: 458.5 AIC: 470.565.4 Summary of Fit
> summary(myfit)
Call:
glm(formula = admit ~ gre + gpa + rank, family = "binomial",
data = mydata)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6268 -0.8662 -0.6388 1.1490 2.0790
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.989979 1.139951 -3.500 0.000465 ***
gre 0.002264 0.001094 2.070 0.038465 *
gpa 0.804038 0.331819 2.423 0.015388 *
rank2 -0.675443 0.316490 -2.134 0.032829 *
rank3 -1.340204 0.345306 -3.881 0.000104 ***
rank4 -1.551464 0.417832 -3.713 0.000205 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 499.98 on 399 degrees of freedom
Residual deviance: 458.52 on 394 degrees of freedom
AIC: 470.52
Number of Fisher Scoring iterations: 465.5 ANOVA of Fit
> anova(myfit, test="Chisq")
Analysis of Deviance Table
Model: binomial, link: logit
Response: admit
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev Pr(>Chi)
NULL 399 499.98
gre 1 13.9204 398 486.06 0.0001907 ***
gpa 1 5.7122 397 480.34 0.0168478 *
rank 3 21.8265 394 458.52 7.088e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> anova(myfit, test="LRT")
Analysis of Deviance Table
Model: binomial, link: logit
Response: admit
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev Pr(>Chi)
NULL 399 499.98
gre 1 13.9204 398 486.06 0.0001907 ***
gpa 1 5.7122 397 480.34 0.0168478 *
rank 3 21.8265 394 458.52 7.088e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 165.6 Example: Contraceptive Use
> cuse <-
+ read.table("http://data.princeton.edu/wws509/datasets/cuse.dat",
+ header=TRUE)
> dim(cuse)
[1] 16 5
> head(cuse)
age education wantsMore notUsing using
1 <25 low yes 53 6
2 <25 low no 10 4
3 <25 high yes 212 52
4 <25 high no 50 10
5 25-29 low yes 60 14
6 25-29 low no 19 10Data and analysis courtesy of http://data.princeton.edu/R/glms.html.
65.7 A Different Format
Note that in this data set there are multiple observations per explanatory variable configuration.
The last two columns of the data frame count the successes and failures per configuration.
> head(cuse)
age education wantsMore notUsing using
1 <25 low yes 53 6
2 <25 low no 10 4
3 <25 high yes 212 52
4 <25 high no 50 10
5 25-29 low yes 60 14
6 25-29 low no 19 1065.8 Fitting the Model
When this is the case, we call the glm() function slighlty differently.
> myfit <- glm(cbind(using, notUsing) ~ age + education + wantsMore,
+ data=cuse, family = binomial)
> myfit
Call: glm(formula = cbind(using, notUsing) ~ age + education + wantsMore,
family = binomial, data = cuse)
Coefficients:
(Intercept) age25-29 age30-39 age40-49 educationlow
-0.8082 0.3894 0.9086 1.1892 -0.3250
wantsMoreyes
-0.8330
Degrees of Freedom: 15 Total (i.e. Null); 10 Residual
Null Deviance: 165.8
Residual Deviance: 29.92 AIC: 113.465.9 Summary of Fit
> summary(myfit)
Call:
glm(formula = cbind(using, notUsing) ~ age + education + wantsMore,
family = binomial, data = cuse)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.5148 -0.9376 0.2408 0.9822 1.7333
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.8082 0.1590 -5.083 3.71e-07 ***
age25-29 0.3894 0.1759 2.214 0.02681 *
age30-39 0.9086 0.1646 5.519 3.40e-08 ***
age40-49 1.1892 0.2144 5.546 2.92e-08 ***
educationlow -0.3250 0.1240 -2.620 0.00879 **
wantsMoreyes -0.8330 0.1175 -7.091 1.33e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 165.772 on 15 degrees of freedom
Residual deviance: 29.917 on 10 degrees of freedom
AIC: 113.43
Number of Fisher Scoring iterations: 465.10 ANOVA of Fit
> anova(myfit)
Analysis of Deviance Table
Model: binomial, link: logit
Response: cbind(using, notUsing)
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev
NULL 15 165.772
age 3 79.192 12 86.581
education 1 6.162 11 80.418
wantsMore 1 50.501 10 29.91765.11 More on this Data Set
See http://data.princeton.edu/R/glms.html for more on fitting logistic regression to this data set.
A number of interesting choices are made that reveal more about the data.