76 Lasso Regression

76.1 Motivation

One drawback of the ridge regression approach is that coefficients will be small, but they will be nonzero.

An alternative appraoch is the lasso, which stands for “Least Absolute Shrinkage and Selection Operator”.

This performs a similar optimization as ridge, but with an \(\ell_1\) penalty instead. This changes the geometry of the problem so that coefficients may be zero.

76.2 Optimization Goal

Starting with the OLS model assumptions again, we wish to find \({\boldsymbol{\beta}}\) that minimizes

\[ \sum_{j=1}^n \left(y_j - \sum_{i=1}^m \beta_{i} x_{ij}\right)^2 + \lambda \sum_{k=1}^m |\beta_k|. \]

Note that \(\sum_{k=1}^m |\beta_k| = \| {\boldsymbol{\beta}}\|_1\), which is the \(\ell_1\) vector norm.

As before, the paramater \(\lambda\) is a tuning paramater that controls how much shrinkage and selection occurs.

76.3 Solution

There is no closed form solution to this optimization problem, so it must be solved numerically.

Originally, a quadratic programming solution was proposed with has \(O(n 2^m)\) operations.

Then a least angle regression solution reduced the solution to \(O(nm^2)\) operations.

Modern coordinate descent methods have further reduced this to \(O(nm)\) operations.

76.4 Preprocessing

Implicitly…

We mean center \({\boldsymbol{y}}\).

We also mean center and standard deviation scale each explanatory variable. Why?

Let’s return to the diabetes data set. To do lasso regression, we set alpha=1.

> lassofit <- glmnetUtils::glmnet(y ~ ., data=df, alpha=1)
> plot(lassofit)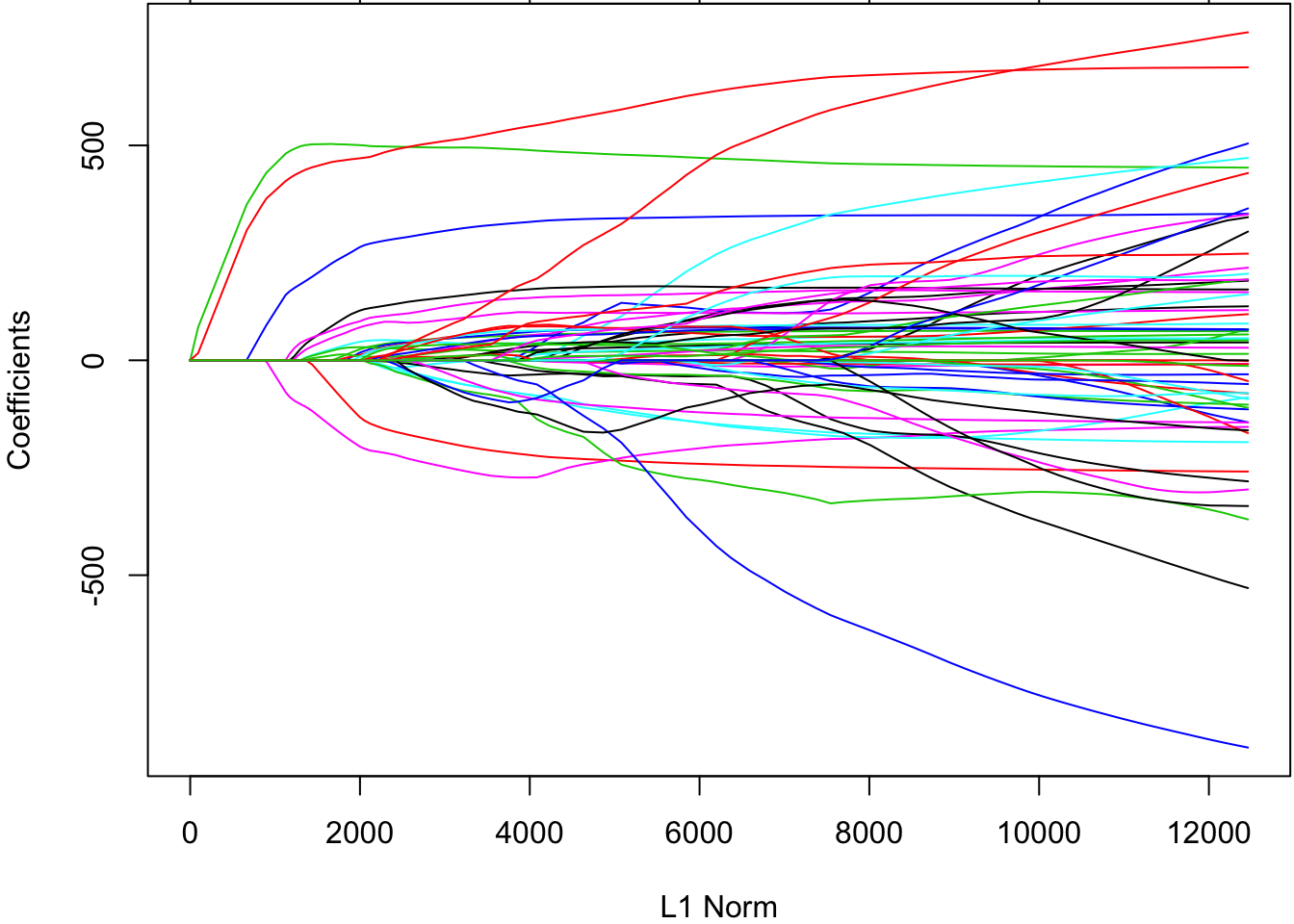

Cross-validation to tune the shrinkage parameter.

> cvlassofit <- glmnetUtils::cv.glmnet(y ~ ., data=df, alpha=1)
> plot(cvlassofit)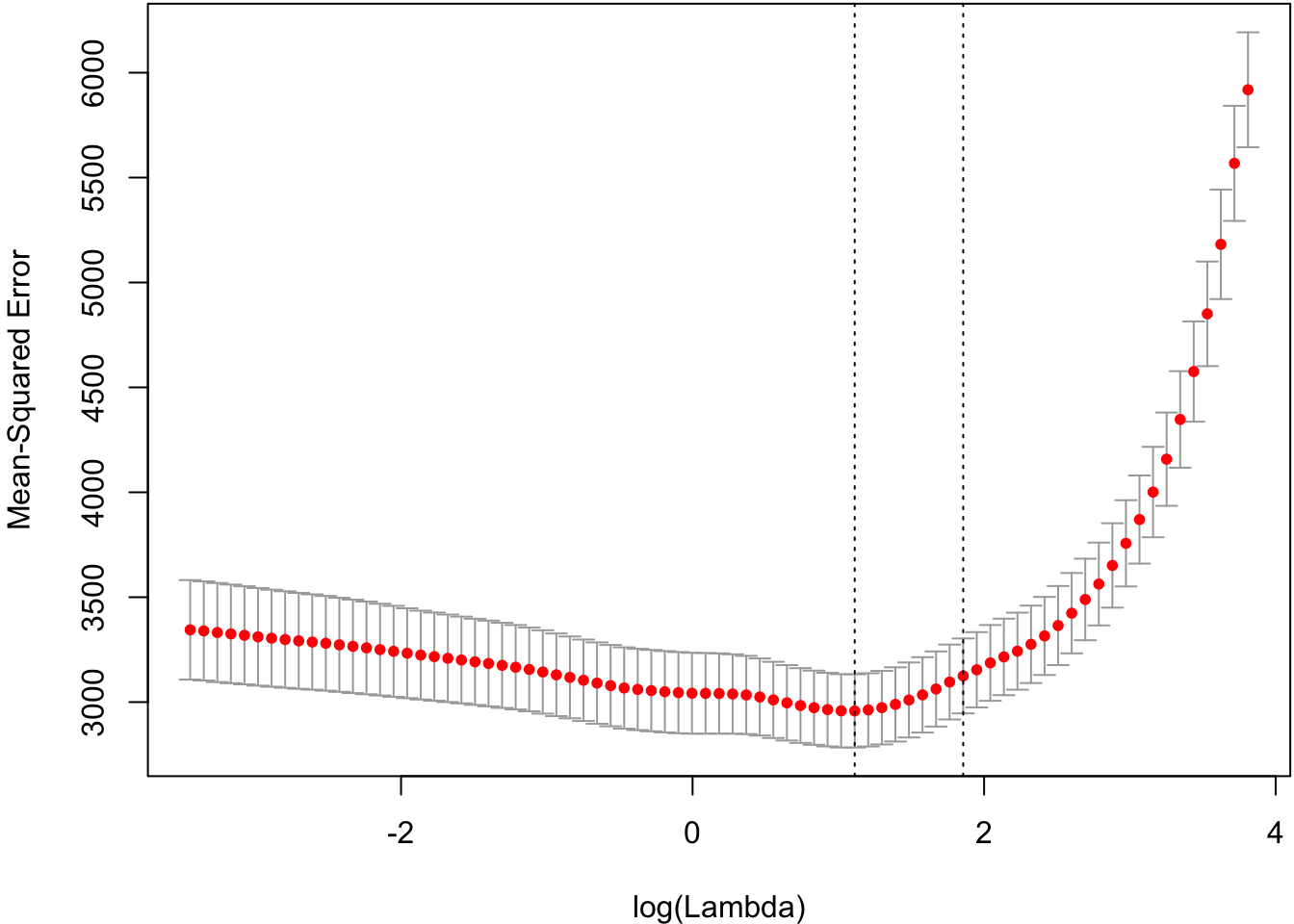

76.5 Bayesian Interpretation

The ridge regression solution is equivalent to maximizing

\[ -\frac{1}{2\sigma^2}\sum_{j=1}^n \left(y_j - \sum_{i=1}^m \beta_{i} x_{ij}\right)^2 - \frac{\lambda}{2\sigma^2} \sum_{k=1}^m |\beta_k| \]

which means it can be interpreted as the MAP solution with a Exponential prior on the \(\beta_i\) values.

76.6 Inference

Inference on the lasso model fit is difficult. However, there has been recent progress.

One idea proposes a conditional covariance statistic, but this requires all explanatory variables to be uncorrelated.

Another idea called the knockoff filter controls the false discovery rate and allows for correlation among explanatory variables.

Both of these ideas have some restrictive assumptions and require the number of observations to exceed the number of explanatory variables, \(n > m\).

76.7 GLMs

The glmnet library (and the glmnetUtils wrapper library) allow one to perform lasso regression on generalized linear models.

A penalized maximum likelihood estimate is calculated based on

\[ -\lambda \sum_{i=1}^m |\beta_i| \]

added to the log-likelihood.