68 Generalized Additive Models
68.1 Ordinary Least Squares
Recall that OLS estimates the model
\[ \begin{aligned} Y_i & = \beta_1 X_{i1} + \beta_2 X_{i2} + \ldots + \beta_p X_{ip} + E_i \\ & = {\boldsymbol{X}}_i {\boldsymbol{\beta}}+ E_i \end{aligned} \]
where \({\operatorname{E}}[{\boldsymbol{E}}| {\boldsymbol{X}}] = {\boldsymbol{0}}\) and \({\operatorname{Cov}}({\boldsymbol{E}}| {\boldsymbol{X}}) = \sigma^2 {\boldsymbol{I}}\).
68.2 Additive Models
The additive model (which could also be called “ordinary nonparametric additive regression”) is of the form
\[ \begin{aligned} Y_i & = s_1(X_{i1}) + s_2(X_{i2}) + \ldots + s_p(X_{ip}) + E_i \\ & = \sum_{j=1}^p s_j(X_{ij}) + E_i \end{aligned} \]
where the \(s_j(\cdot)\) for \(j = 1, \ldots, p\) are a set of nonparametric (or flexible) functions. Again, we assume that \({\operatorname{E}}[{\boldsymbol{E}}| {\boldsymbol{X}}] = {\boldsymbol{0}}\) and \({\operatorname{Cov}}({\boldsymbol{E}}| {\boldsymbol{X}}) = \sigma^2 {\boldsymbol{I}}\).
68.3 Backfitting
The additive model can be fit through a technique called backfitting.
- Intialize \(s^{(0)}_j(x)\) for \(j = 1, \ldots, p\).
- For \(t=1, 2, \ldots\), fit \(s_j^{(t)}(x)\) on response variable \[y_i - \sum_{k \not= j} s_k^{(t-1)}(x_{ij}).\]
- Repeat until convergence.
Note that some extra steps have to be taken to deal with the intercept.
68.4 GAM Definition
\(Y | {\boldsymbol{X}}\) is distributed according to an exponential family distribution. The extension of additive models to this family of response variable is called generalized additive models (GAMs). The model is of the form
\[ g\left({\operatorname{E}}[Y_i | {\boldsymbol{X}}_i]\right) = \sum_{j=1}^p s_j(X_{ij}) \]
where \(g(\cdot)\) is the link function and the \(s_j(\cdot)\) are flexible and/or nonparametric functions.
68.5 Overview of Fitting GAMs
Fitting GAMs involves putting together the following three tools:
- We know how to fit a GLM via IRLS
- We know how to fit a smoother of a single explanatory variable via a least squares solution, as seen for the NCS
- We know how to combine additive smoothers by backfitting
68.6 GAMs in R
Three common ways to fit GAMs in R:
- Utilize
glm()on explanatory variables constructed fromns()orbs() - The
gamlibrary - The
mgcvlibrary
68.7 Example
> set.seed(508)
> x1 <- seq(1, 10, length.out=50)
> n <- length(x1)
> x2 <- rnorm(n)
> f <- 4*log(x1) + sin(x1) - 7 + 0.5*x2
> p <- exp(f)/(1+exp(f))
> summary(p)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.001842 0.074171 0.310674 0.436162 0.860387 0.944761
> y <- rbinom(n, size=1, prob=p)
> mean(y)
[1] 0.42
> df <- data.frame(x1=x1, x2=x2, y=y)Here, we use the gam() function from the mgcv library. It automates choosing the smoothness of the splines.
> library(mgcv)
> mygam <- gam(y ~ s(x1) + s(x2), family = binomial(), data=df)
> library(broom)
> tidy(mygam)
# A tibble: 2 x 5
term edf ref.df statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 s(x1) 1.87 2.37 12.7 0.00531
2 s(x2) 1.00 1.00 1.16 0.281 > summary(mygam)
Family: binomial
Link function: logit
Formula:
y ~ s(x1) + s(x2)
Parametric coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.1380 0.6723 -1.693 0.0905 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df Chi.sq p-value
s(x1) 1.87 2.375 12.743 0.00531 **
s(x2) 1.00 1.000 1.163 0.28084
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.488 Deviance explained = 47%
UBRE = -0.12392 Scale est. = 1 n = 50True probabilities vs. estimated probabilities.
> plot(p, mygam$fitted.values, pch=19); abline(0,1)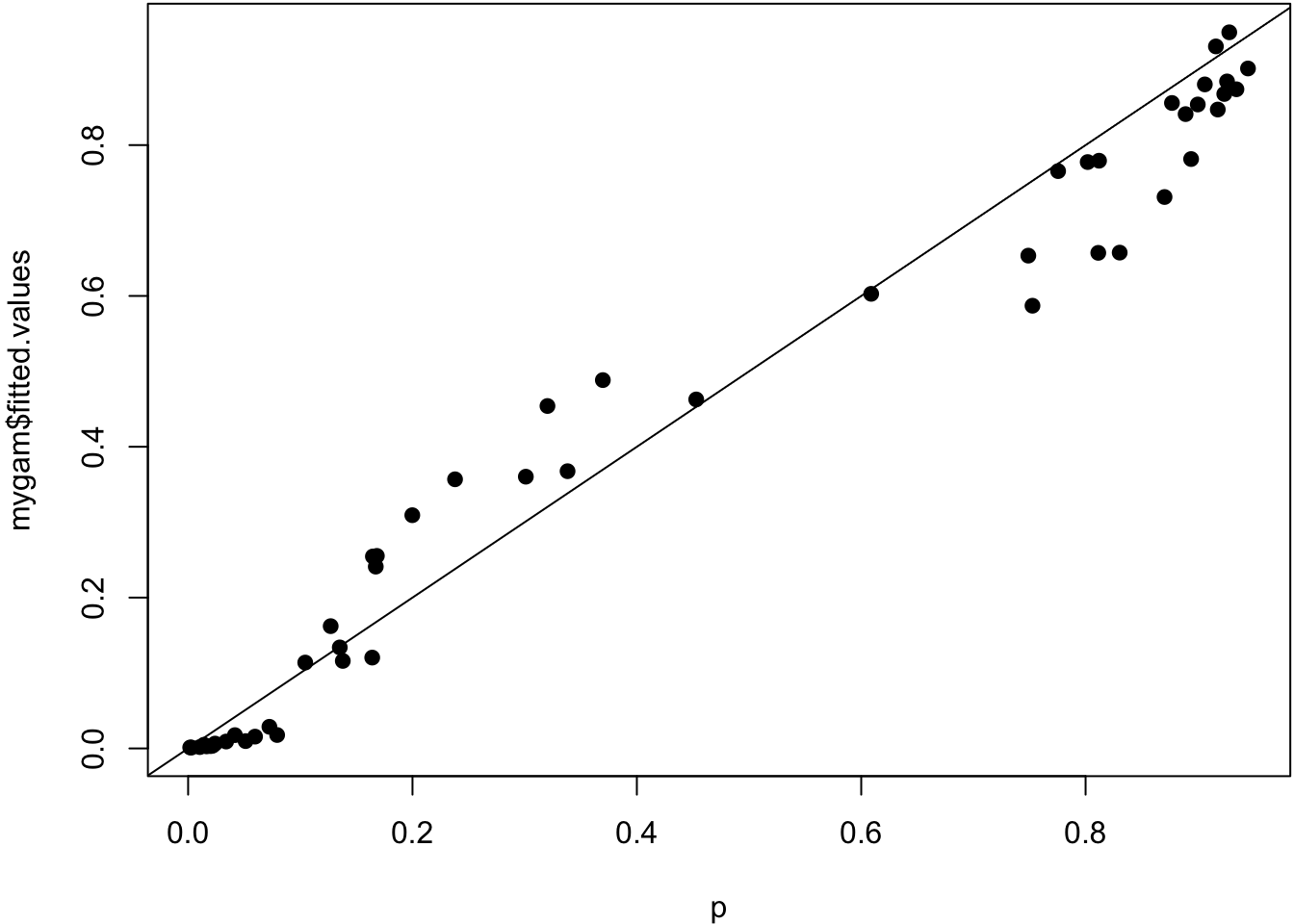
Smoother estimated for x1.
> plot(mygam, select=1)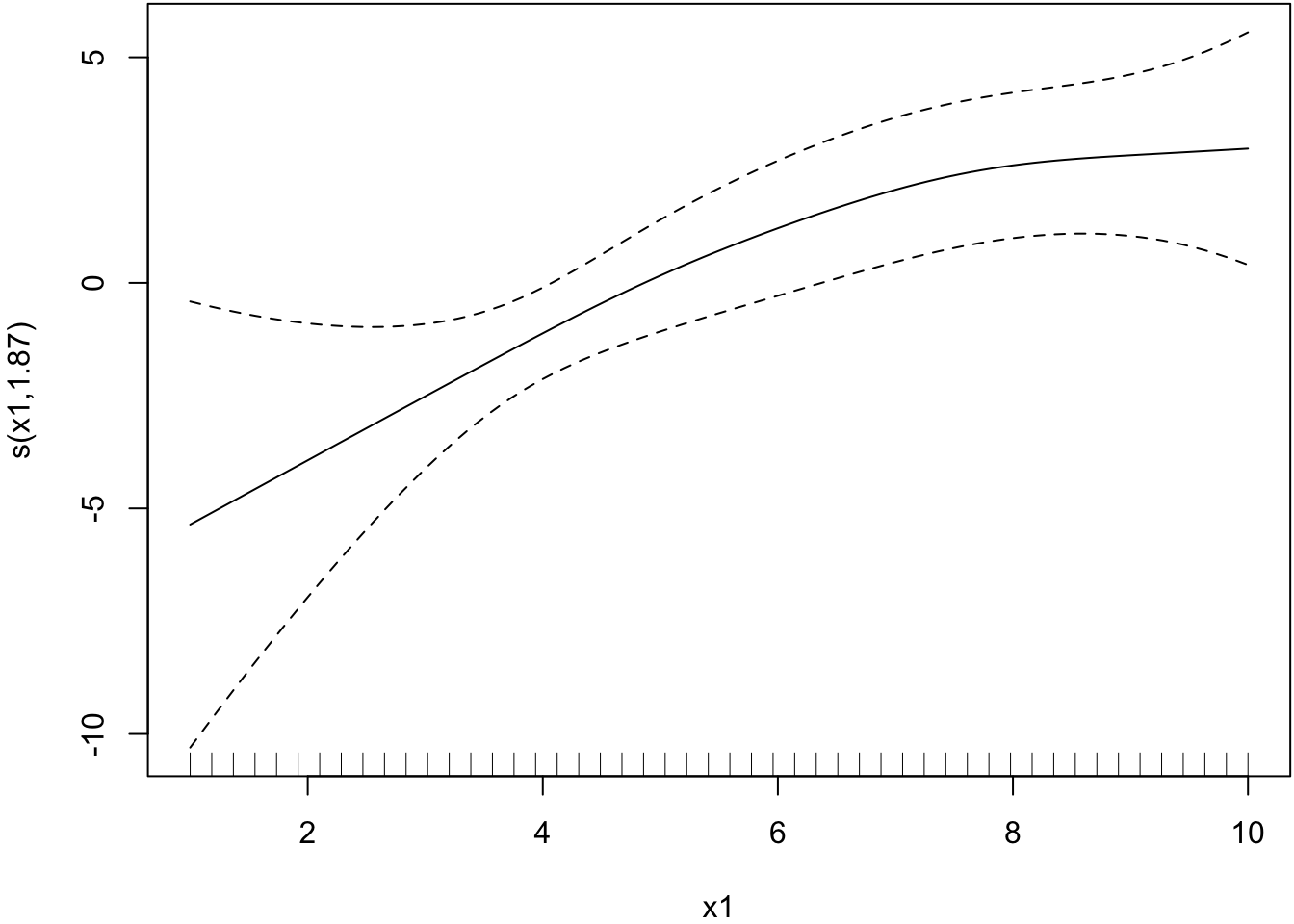
Smoother estimated for x2.
> plot(mygam, select=2)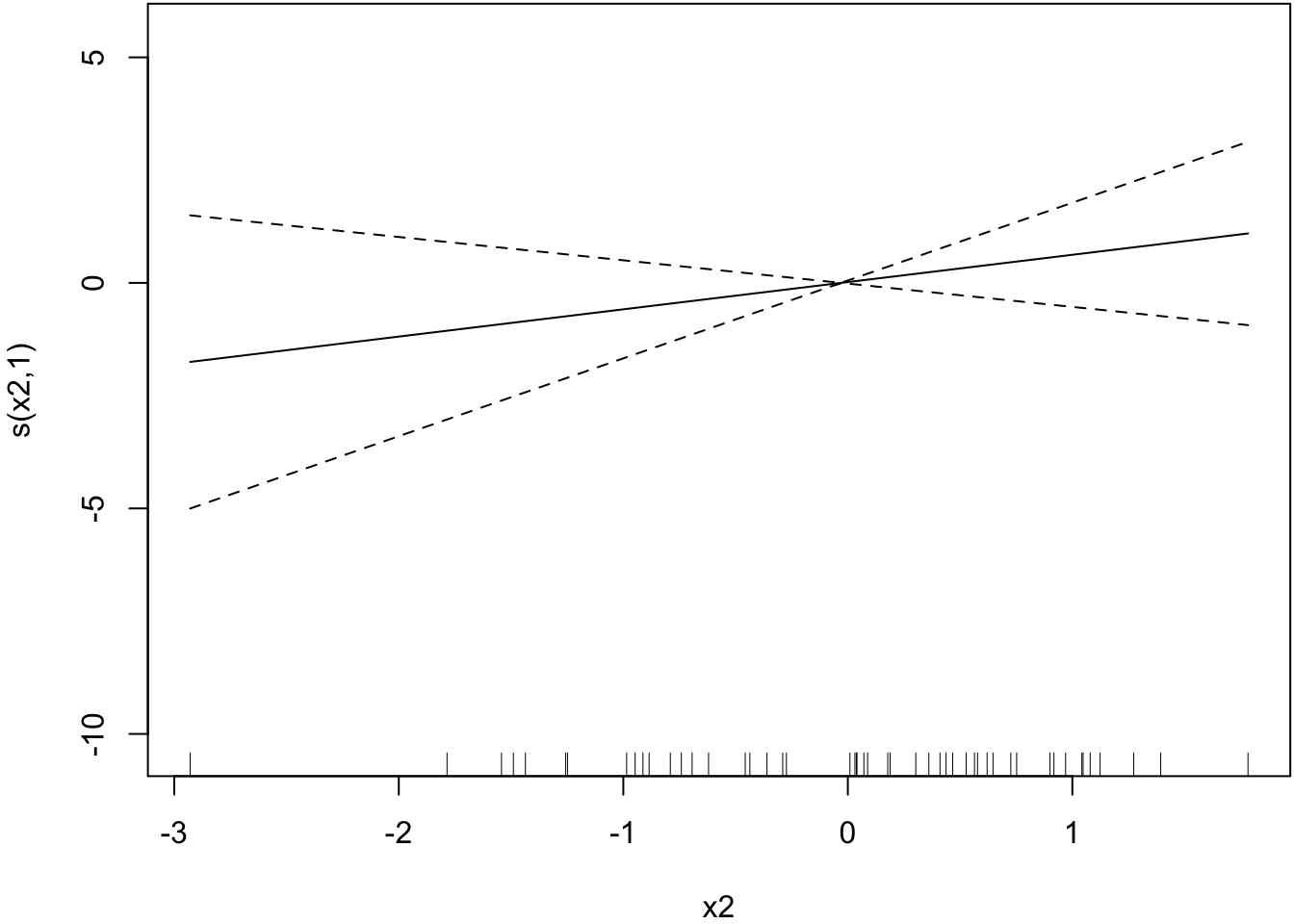
Here, we use the glm() function and include as an explanatory variable a NCS built from the ns() function from the splines library. We include a df argument in the ns() call.
> library(splines)
> myglm <- glm(y ~ ns(x1, df=2) + x2, family = binomial(), data=df)
> tidy(myglm)
# A tibble: 4 x 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -10.9 5.31 -2.06 0.0396
2 ns(x1, df = 2)1 21.4 10.1 2.11 0.0348
3 ns(x1, df = 2)2 6.33 2.11 3.00 0.00272
4 x2 0.734 0.609 1.21 0.228 The spline basis evaluated at x1 values.
> ns(x1, df=2)
1 2
[1,] 0.00000000 0.00000000
[2,] 0.03114456 -0.02075171
[3,] 0.06220870 -0.04138180
[4,] 0.09311200 -0.06176867
[5,] 0.12377405 -0.08179071
[6,] 0.15411442 -0.10132630
[7,] 0.18405270 -0.12025384
[8,] 0.21350847 -0.13845171
[9,] 0.24240131 -0.15579831
[10,] 0.27065081 -0.17217201
[11,] 0.29817654 -0.18745121
[12,] 0.32489808 -0.20151430
[13,] 0.35073503 -0.21423967
[14,] 0.37560695 -0.22550571
[15,] 0.39943343 -0.23519080
[16,] 0.42213406 -0.24317334
[17,] 0.44362840 -0.24933170
[18,] 0.46383606 -0.25354429
[19,] 0.48267660 -0.25568949
[20,] 0.50006961 -0.25564569
[21,] 0.51593467 -0.25329128
[22,] 0.53019136 -0.24850464
[23,] 0.54275927 -0.24116417
[24,] 0.55355797 -0.23114825
[25,] 0.56250705 -0.21833528
[26,] 0.56952943 -0.20260871
[27,] 0.57462513 -0.18396854
[28,] 0.57787120 -0.16253131
[29,] 0.57934806 -0.13841863
[30,] 0.57913614 -0.11175212
[31,] 0.57731586 -0.08265339
[32,] 0.57396762 -0.05124405
[33,] 0.56917185 -0.01764570
[34,] 0.56300897 0.01802003
[35,] 0.55555939 0.05563154
[36,] 0.54690354 0.09506722
[37,] 0.53712183 0.13620546
[38,] 0.52629468 0.17892464
[39,] 0.51450251 0.22310315
[40,] 0.50182573 0.26861939
[41,] 0.48834478 0.31535174
[42,] 0.47414005 0.36317859
[43,] 0.45929198 0.41197833
[44,] 0.44388099 0.46162934
[45,] 0.42798748 0.51201003
[46,] 0.41169188 0.56299877
[47,] 0.39507460 0.61447395
[48,] 0.37821607 0.66631397
[49,] 0.36119670 0.71839720
[50,] 0.34409692 0.77060206
attr(,"degree")
[1] 3
attr(,"knots")
50%
5.5
attr(,"Boundary.knots")
[1] 1 10
attr(,"intercept")
[1] FALSE
attr(,"class")
[1] "ns" "basis" "matrix"Plot of basis function values vs x1.
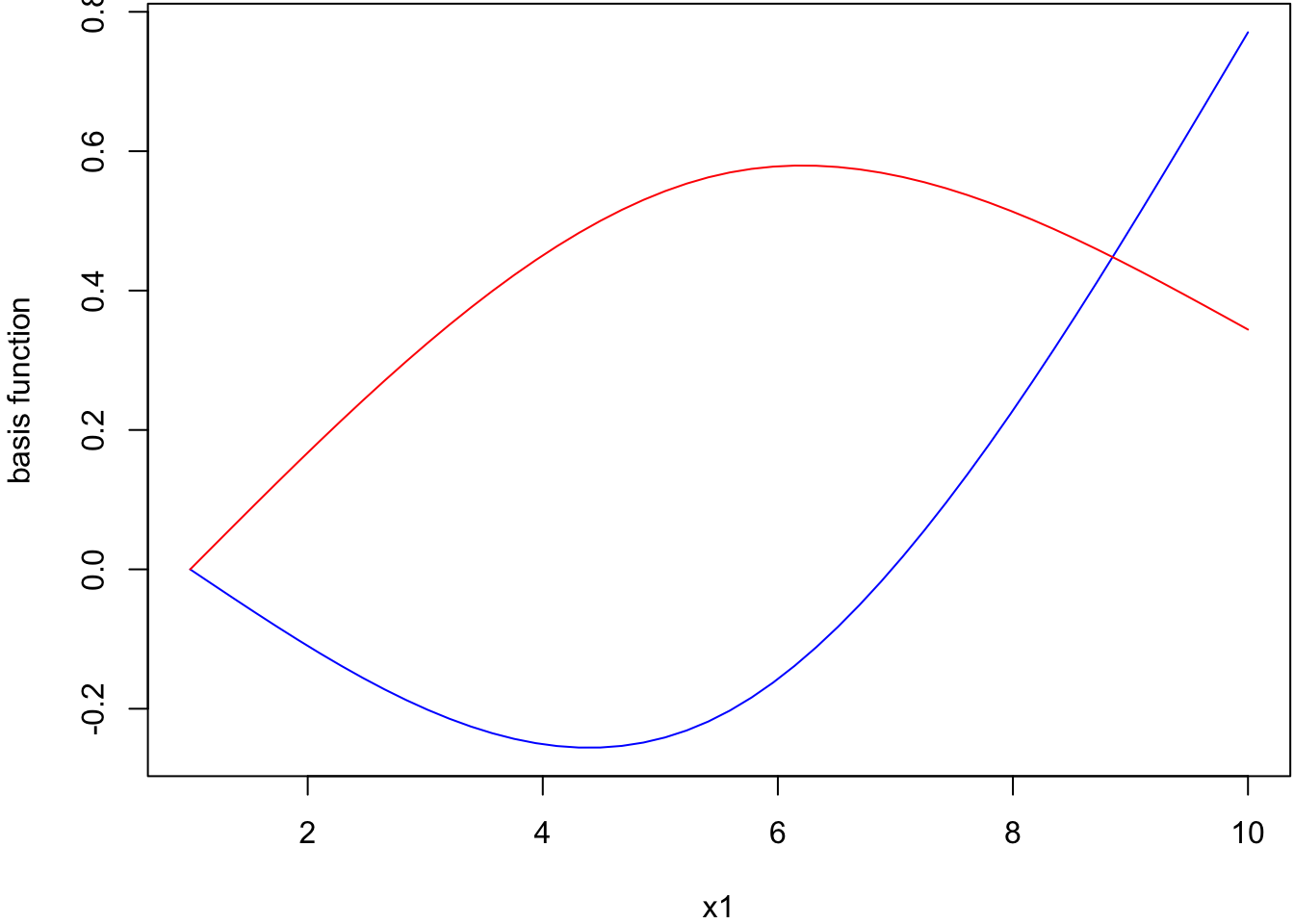
> summary(myglm)
Call:
glm(formula = y ~ ns(x1, df = 2) + x2, family = binomial(), data = df)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.0214 -0.3730 -0.0162 0.5762 1.7616
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -10.9229 5.3079 -2.058 0.03960 *
ns(x1, df = 2)1 21.3848 10.1318 2.111 0.03480 *
ns(x1, df = 2)2 6.3266 2.1103 2.998 0.00272 **
x2 0.7342 0.6089 1.206 0.22795
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 68.029 on 49 degrees of freedom
Residual deviance: 35.682 on 46 degrees of freedom
AIC: 43.682
Number of Fisher Scoring iterations: 7> anova(myglm, test="LRT")
Analysis of Deviance Table
Model: binomial, link: logit
Response: y
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev Pr(>Chi)
NULL 49 68.029
ns(x1, df = 2) 2 30.755 47 37.274 2.097e-07 ***
x2 1 1.592 46 35.682 0.207
---
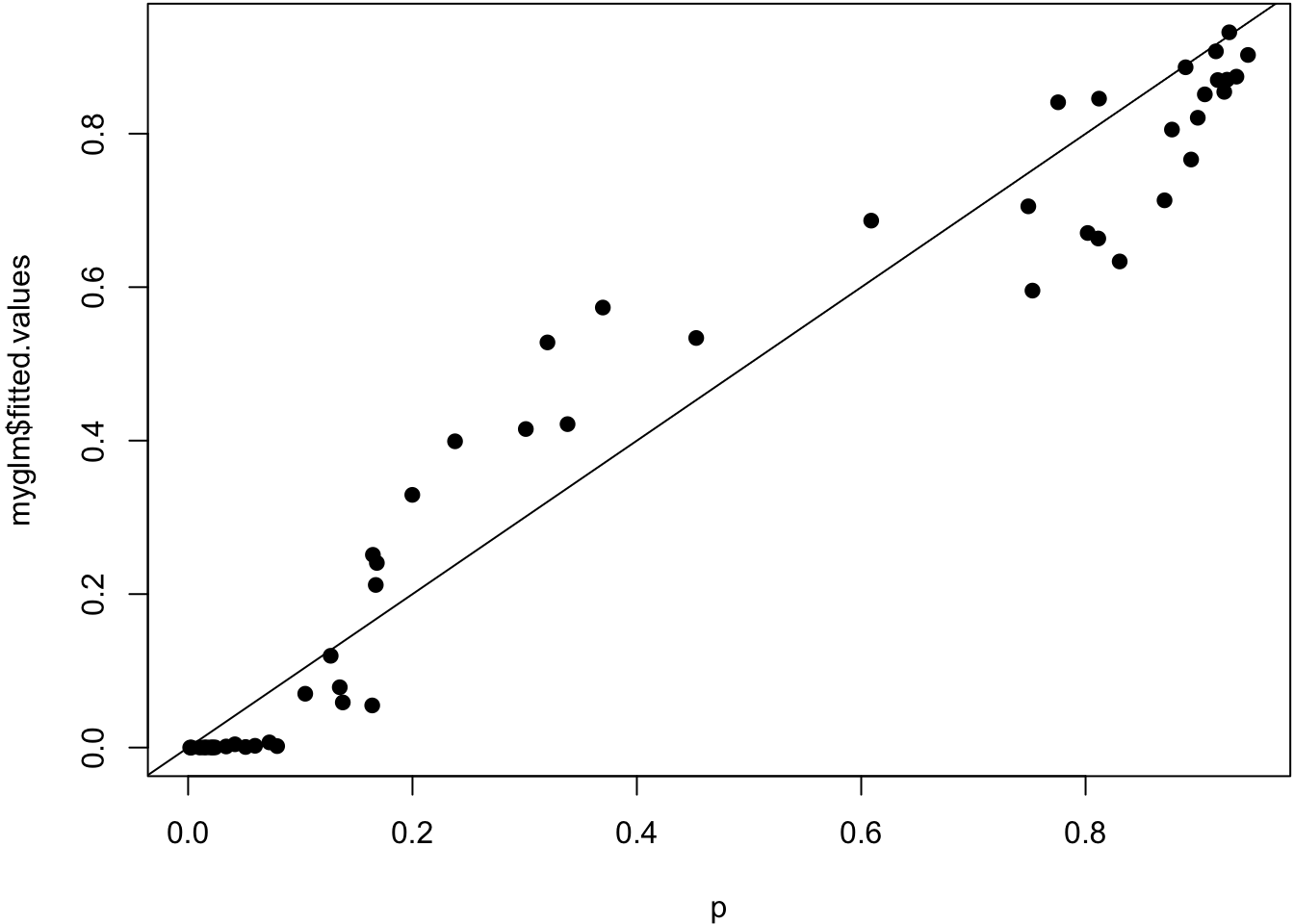
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1True probabilities vs. estimated probabilities.
> plot(p, myglm$fitted.values, pch=19); abline(0,1)