QCB 508 – Week 3
John D. Storey
Spring 2017
Exploratory Data Analysis
What is EDA?
Exploratory data analysis (EDA) is the process of analzying data to uncover their key features.
John Tukey pioneered this framework, writing a seminal book on the topic (called Exploratory Data Analysis).
EDA involves calculating numerical summaries of data, visualizing data in a variety of ways, and considering interesting data points.
Before any model fitting is done to data, some exploratory data analysis should always be performed.
Data science seems to focus much more on EDA than traditional statistics.
Descriptive Statistics Examples
Facebook’s Visualizing Friendships (side note: a discussion)
Hans Rosling: Debunking third-world myths with the best stats you’ve ever seen
Flowing Data’s A Day in the Life of Americans
Components of EDA
EDA involves calculating quantities and visualizing data for:
- Checking the n’s
- Checking for missing data
- Characterizing the distributional properties of the data
- Characterizing relationships among variables and observations
- Dimension reduction
- Model formulation
- Hypothesis generation
… and there are possible many more activities one can do.
R4DS Workflow
Which of the following components of the R4DS workflow involve EDA?
- Import
- Tidy
- Transform \(\leftrightarrow\) Visualize \(\leftrightarrow\) Model (iterate)
- Communicate
Data Sets
Data mtcars
Load the mtcars data set:
> library("tidyverse") # why load tidyverse?
> data("mtcars", package="datasets")
> mtcars <- as_tibble(mtcars)
> head(mtcars)
# A tibble: 6 × 11
mpg cyl disp hp drat wt qsec vs am gear
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 21.0 6 160 110 3.90 2.620 16.46 0 1 4
2 21.0 6 160 110 3.90 2.875 17.02 0 1 4
3 22.8 4 108 93 3.85 2.320 18.61 1 1 4
4 21.4 6 258 110 3.08 3.215 19.44 1 0 3
5 18.7 8 360 175 3.15 3.440 17.02 0 0 3
6 18.1 6 225 105 2.76 3.460 20.22 1 0 3
# ... with 1 more variables: carb <dbl>Data mpg
Load the mpg data set:
> data("mpg", package="ggplot2")
> head(mpg)
# A tibble: 6 × 11
manufacturer model displ year cyl trans drv cty
<chr> <chr> <dbl> <int> <int> <chr> <chr> <int>
1 audi a4 1.8 1999 4 auto(l5) f 18
2 audi a4 1.8 1999 4 manual(m5) f 21
3 audi a4 2.0 2008 4 manual(m6) f 20
4 audi a4 2.0 2008 4 auto(av) f 21
5 audi a4 2.8 1999 6 auto(l5) f 16
6 audi a4 2.8 1999 6 manual(m5) f 18
# ... with 3 more variables: hwy <int>, fl <chr>, class <chr>Data diamonds
Load the diamonds data set:
> data("diamonds", package="ggplot2")
> head(diamonds)
# A tibble: 6 × 10
carat cut color clarity depth table price x y
<dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl>
1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98
2 0.21 Premium E SI1 59.8 61 326 3.89 3.84
3 0.23 Good E VS1 56.9 65 327 4.05 4.07
4 0.29 Premium I VS2 62.4 58 334 4.20 4.23
5 0.31 Good J SI2 63.3 58 335 4.34 4.35
6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96
# ... with 1 more variables: z <dbl>Data gapminder
Load the gapminder data set:
> library("gapminder")
> data("gapminder", package="gapminder")
> gapminder <- as_tibble(gapminder)
> head(gapminder)
# A tibble: 6 × 6
country continent year lifeExp pop gdpPercap
<fctr> <fctr> <int> <dbl> <int> <dbl>
1 Afghanistan Asia 1952 28.801 8425333 779.4453
2 Afghanistan Asia 1957 30.332 9240934 820.8530
3 Afghanistan Asia 1962 31.997 10267083 853.1007
4 Afghanistan Asia 1967 34.020 11537966 836.1971
5 Afghanistan Asia 1972 36.088 13079460 739.9811
6 Afghanistan Asia 1977 38.438 14880372 786.1134Numerical Summaries of Data
Useful Summaries
Center: mean, median, mode
Quantiles: percentiles, five number summaries
Spread: standard deviation, variance, interquartile range
Outliers
Shape: skewness, kurtosis
Concordance: correlation, quantile-quantile plots
Measures of Center
Suppose we have data points \(x_1, x_2, \ldots, x_n\).
Mean: \[\overline{x} = \frac{x_1 + x_2 + \cdots + x_n}{n}\]
Median: Order the points \(x_{(1)} \leq x_{(2)} \leq \cdots \leq x_{(n)}\). The median is the middle value:
- \(x_{((n+1)/2)}\) if \(n\) is odd
- \((x_{(n/2)} + x_{(n/2+1)})/2\) if \(n\) is even
Mode: The most frequently repeated value among the data (if any). If there are ties, then there is more than one mode.
Mean, Median, and Mode in R
Let’s calculate these quantities in R.
> mean(mtcars$mpg)
[1] 20.09062
> median(mtcars$mpg)
[1] 19.2
>
> sample_mode <- function(x) {
+ as.numeric(names(which(table(x) == max(table(x)))))
+ }
>
> sample_mode(round(mtcars$mpg))
[1] 15 21It appears there is no R base function for calculating the mode.
Quantiles and Percentiles
The \(p\)th percentile of \(x_1, x_2, \ldots, x_n\) is a number such that \(p\)% of the data are less than this number.
The 25th, 50th, and 75th percentiles are called 1st, 2nd, and 3rd “quartiles”, respectively. These are sometimes denoted as Q1, Q2, and Q3. The median is the 50th percentile aka the 2nd quartile aka Q2.
In general, \(q\)-quantiles are cut points that divide the data into \(q\) approximately equally sized groups. The cut points are the percentiles \(1/q, 2/q, \ldots, (q-1)/q.\)
Five Number Summary
The “five number summary” is the minimum, the three quartiles, and the maximum. This can be calculated via fivenum() and summary(). They can produce different values. Finally, quantile() extracts any set of percentiles.
> fivenum(mtcars$mpg)
[1] 10.40 15.35 19.20 22.80 33.90
> summary(mtcars$mpg)
Min. 1st Qu. Median Mean 3rd Qu. Max.
10.40 15.42 19.20 20.09 22.80 33.90
>
> quantile(mtcars$mpg, prob=seq(0, 1, 0.25))
0% 25% 50% 75% 100%
10.400 15.425 19.200 22.800 33.900 Measures of Spread
The variance, standard deviation (SD), and interquartile range (IQR) measure the “spread” of the data.
Variance: \[s^2 = \frac{\sum_{i=1}^n \left(x_i - \overline{x}\right)^2}{n-1}\]
Standard Deviation: \(s = \sqrt{s^2}\)
Iterquartile Range: IQR \(=\) Q3 \(-\) Q1
The SD and IQR have the same units as the observed data, but the variance is in squared units.
Variance, SD, and IQR in R
Variance:
> var(mtcars$mpg)
[1] 36.3241Standard deviation:
> sd(mtcars$mpg)
[1] 6.026948Interquartile range:
> IQR(mtcars$mpg)
[1] 7.375
> diff(fivenum(mtcars$mpg)[c(2,4)])
[1] 7.45Identifying Outliers
An outlier is an unusual data point. Outliers can be perfectly valid but they can also be due to errors (as can non-outliers).
One must define what is meant by an outlier.
One definition is a data point that less than Q1 or greater than Q3 by 1.5 \(\times\) IQR or more.
Another definition is a data point whose difference from the mean is greater than 3 \(\times\) SD or more. For Normal distributed data (bell curve shaped), the probability of this is less than 0.27%.
Application to mtcars Data
> sd_units <- abs(mtcars$wt - mean(mtcars$wt))/sd(mtcars$wt)
> sum(sd_units > 3)
[1] 0
> max(sd_units)
[1] 2.255336
>
> iqr_outlier_cuts <- fivenum(mtcars$wt)[c(2,4)] +
+ c(-1.5, 1.5)*diff(fivenum(mtcars$wt)[c(2,4)])
> sum(mtcars$wt < iqr_outlier_cuts[1] |
+ mtcars$wt > iqr_outlier_cuts[2])
[1] 2Data Visualization Basics
Plots
- Single variables:
- Barplot
- Boxplot
- Histogram
- Density plot
- Two or more variables:
- Side-by-Side Boxplots
- Stacked Barplot
- Scatterplot
R Base Graphics
- We’ll first plodding through “R base graphics”, which means graphics functions that come with R.
- By default they are very simple. However, they can be customized a lot, but it takes a lot of work.
- Also, the syntax varies significantly among plot types and some think the syntax is not user-friendly.
- We will consider a very highly used graphics package next week, called
ggplot2that provides a “grammar of graphics”. It hits a sweet spot of “flexibility vs. complexity” for many data scientists.
Read the Documentation
For all of the plotting functions covered below, read the help files.
> ?barplot
> ?boxplot
> ?hist
> ?density
> ?plot
> ?legendBarplot
> cyl_tbl <- table(mtcars$cyl)
> barplot(cyl_tbl, xlab="Cylinders", ylab="Count")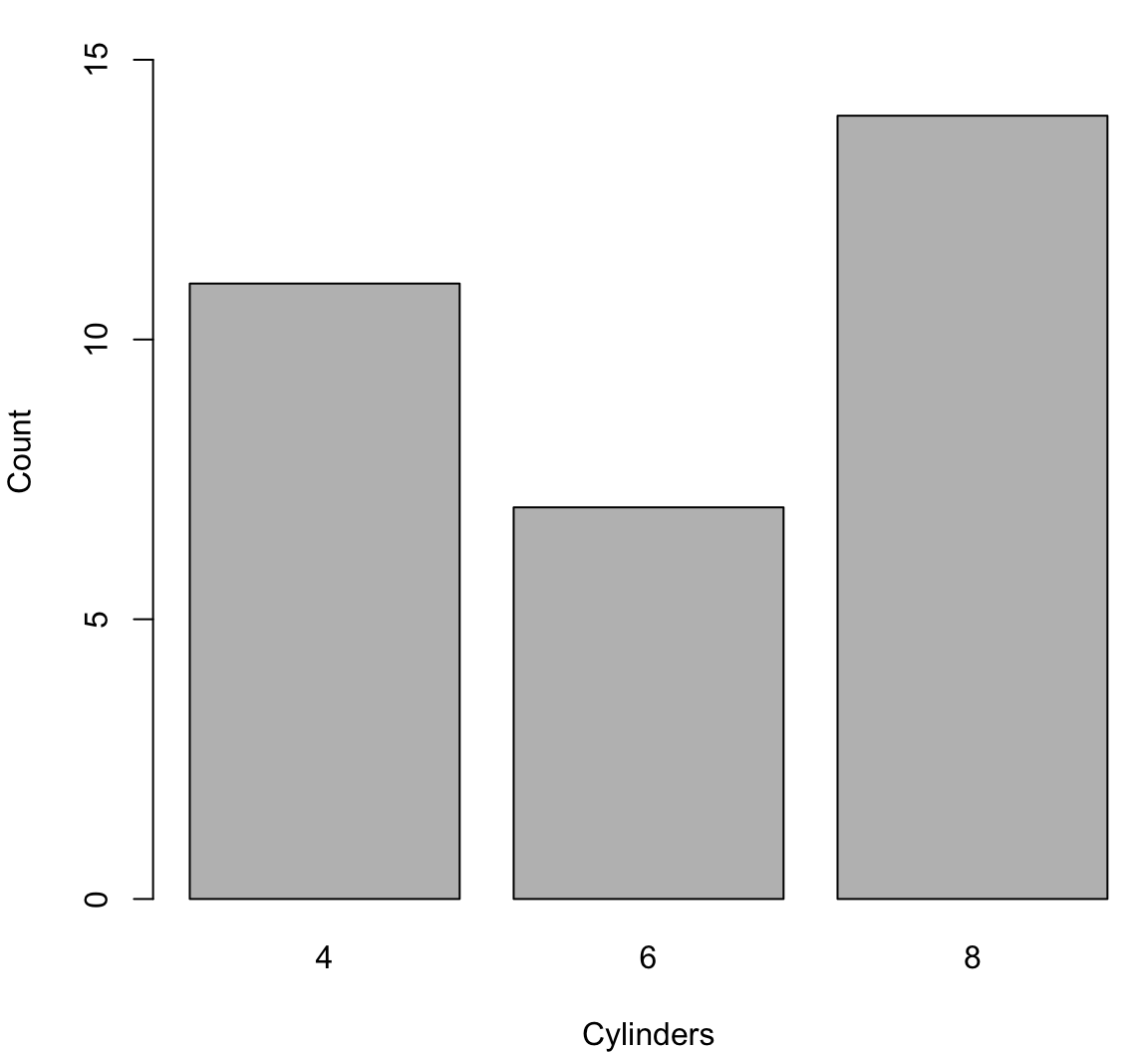
Boxplot
> boxplot(mtcars$mpg, ylab="MPG", col="lightgray")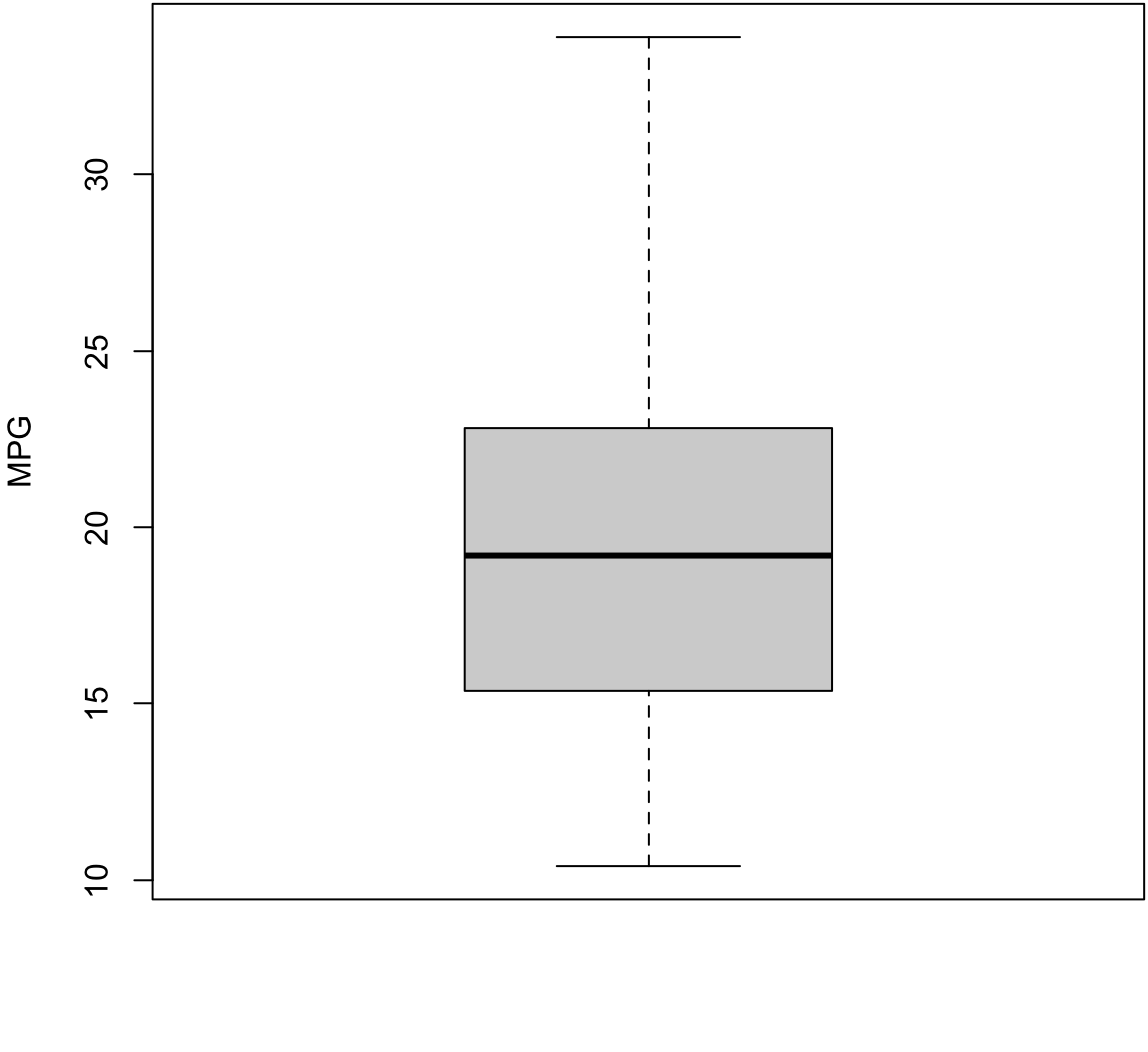
Constructing Boxplots
- The top of the box is Q3
- The line through the middle of the box is the median
- The bottom of the box is Q1
- The top whisker is the minimum of Q3 + 1.5 \(\times\) IQR or the largest data point
- The bottom whisker is the maximum of Q1 - 1.5 \(\times\) IQR or the smallest data point
- Outliers lie outside of (Q1 - 1.5 \(\times\) IQR) or (Q3 + 1.5 \(\times\) IQR), and they are shown as points
- Outliers are calculated using the
fivenum()function
Boxplot with Outliers
> boxplot(mtcars$wt, ylab="Weight (1000 lbs)",
+ col="lightgray")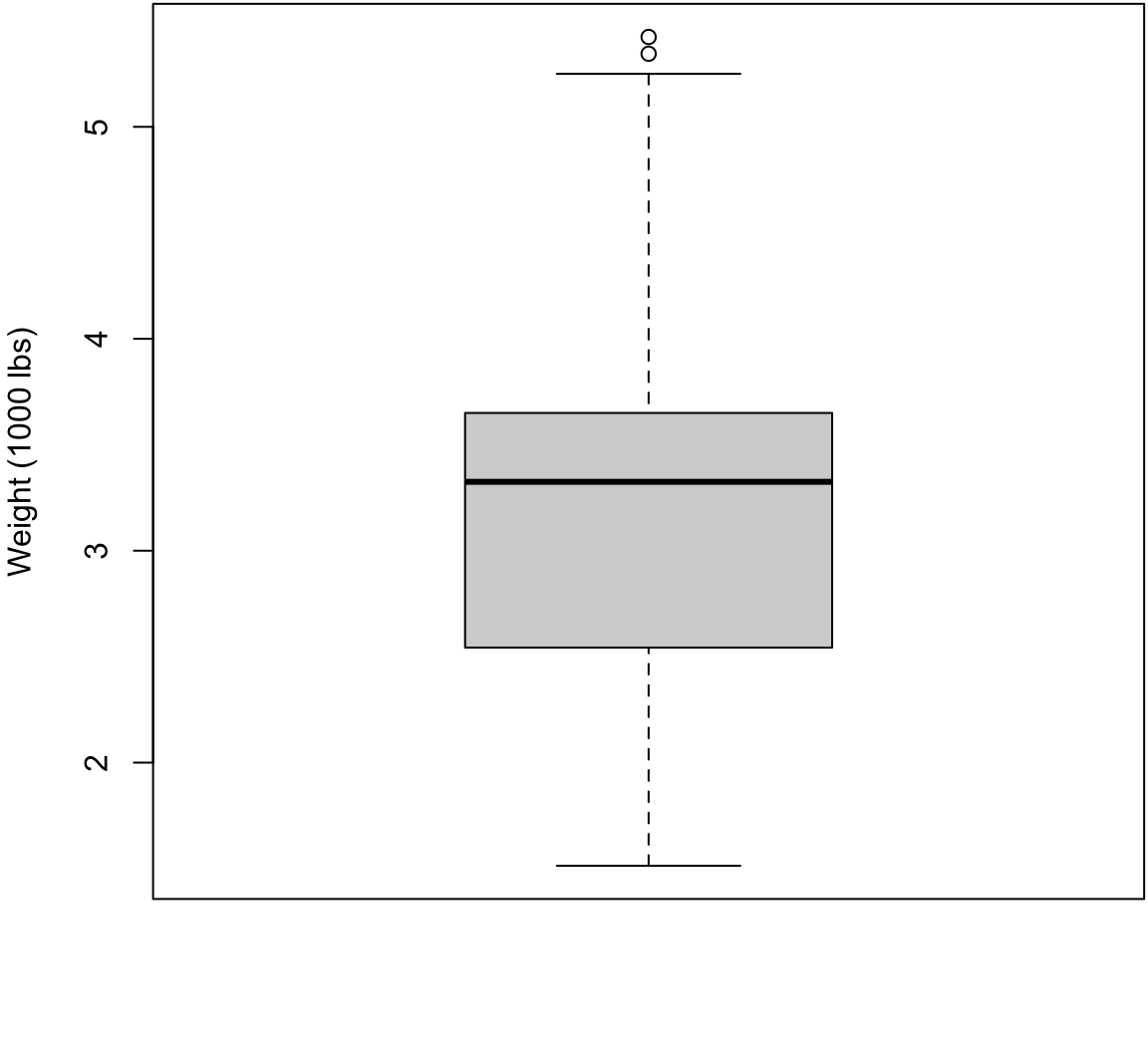
Histogram
> hist(mtcars$mpg, xlab="MPG", main="", col="lightgray")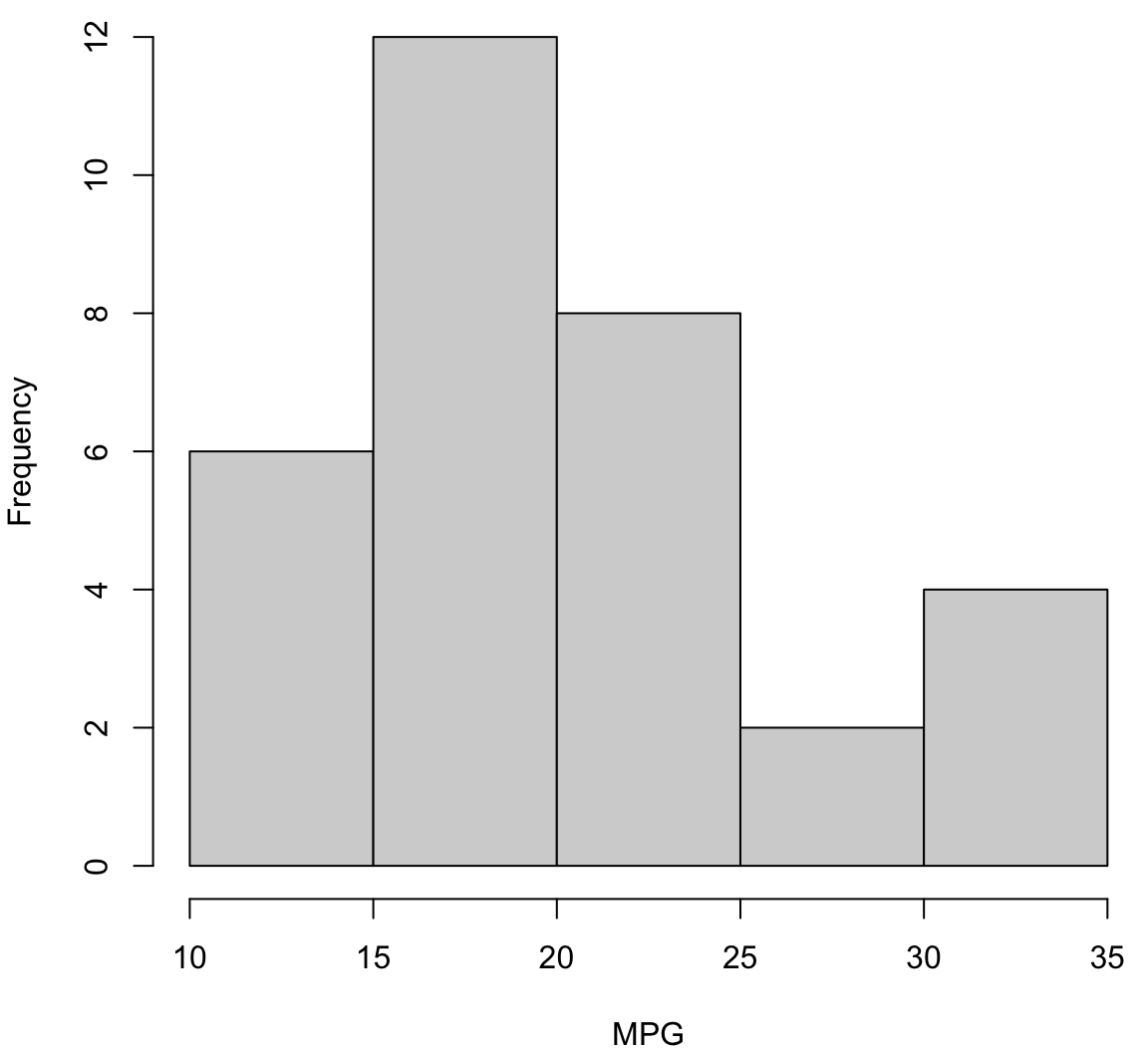
Histogram with More Breaks
> hist(mtcars$mpg, breaks=12, xlab="MPG", main="", col="lightgray")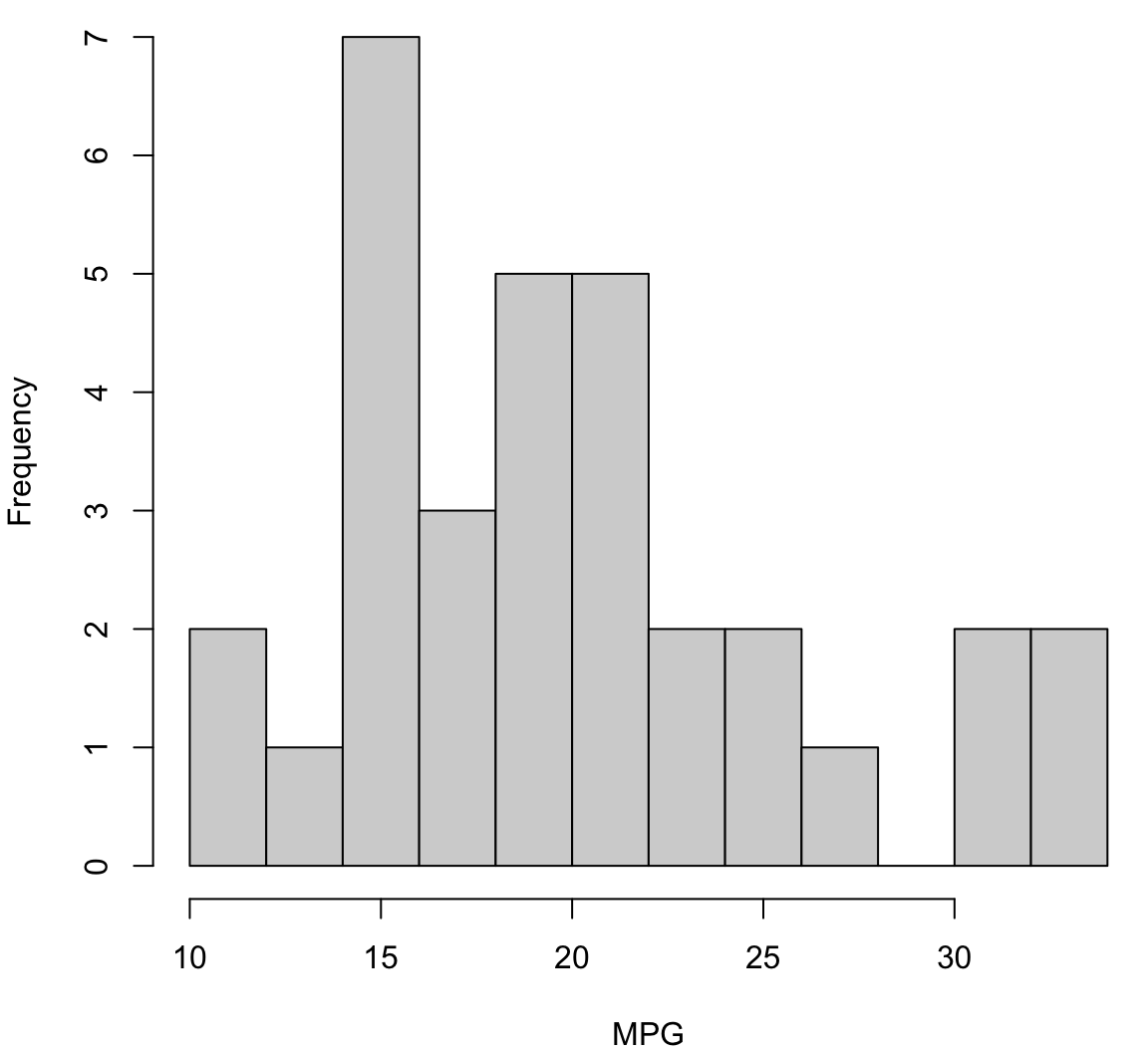
Density Plot
> plot(density(mtcars$mpg), xlab="MPG", main="")
> polygon(density(mtcars$mpg), col="lightgray", border="black")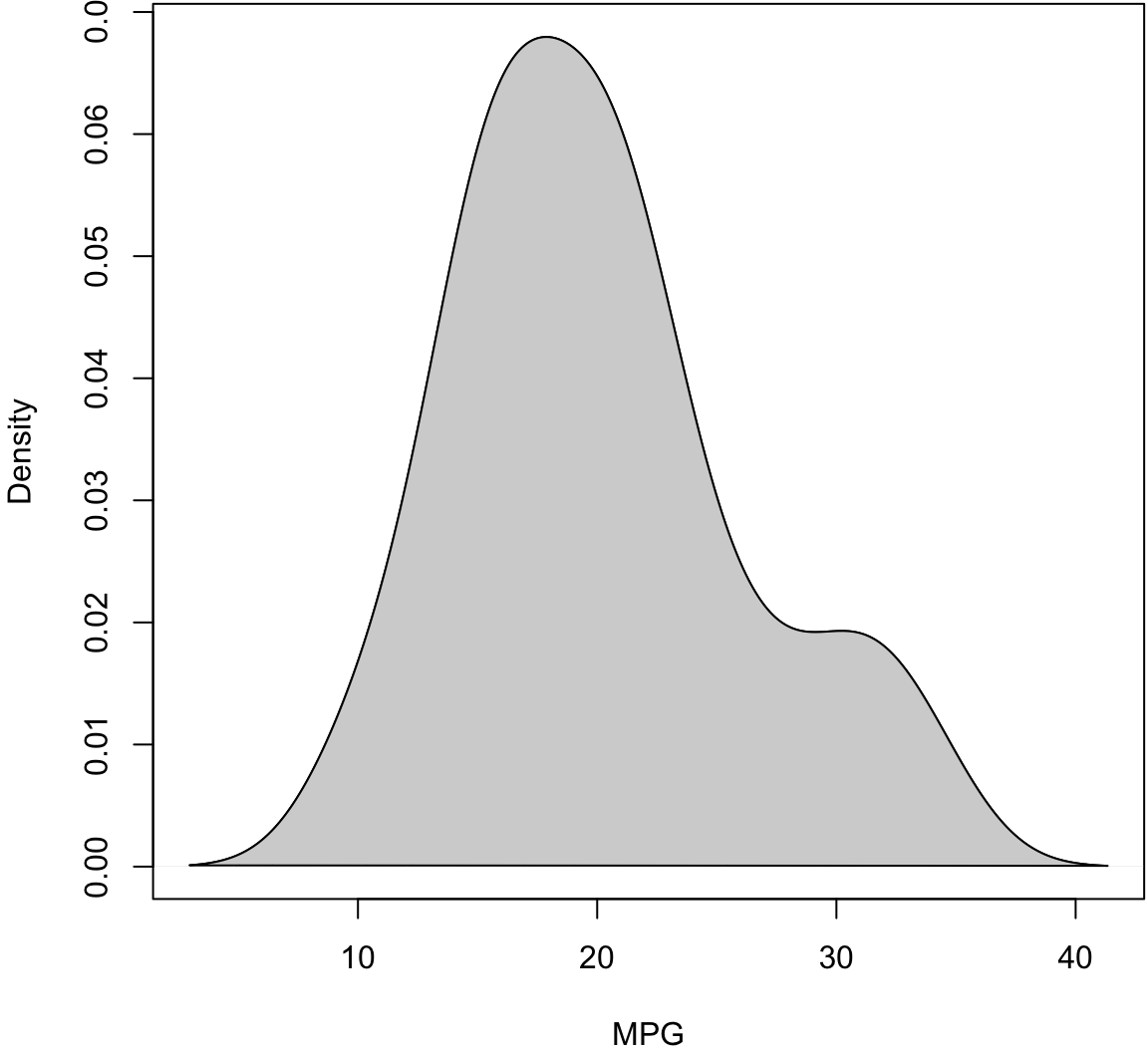
Boxplot (Side-By-Side)
> boxplot(mpg ~ cyl, data=mtcars, xlab="Cylinders",
+ ylab="MPG", col="lightgray")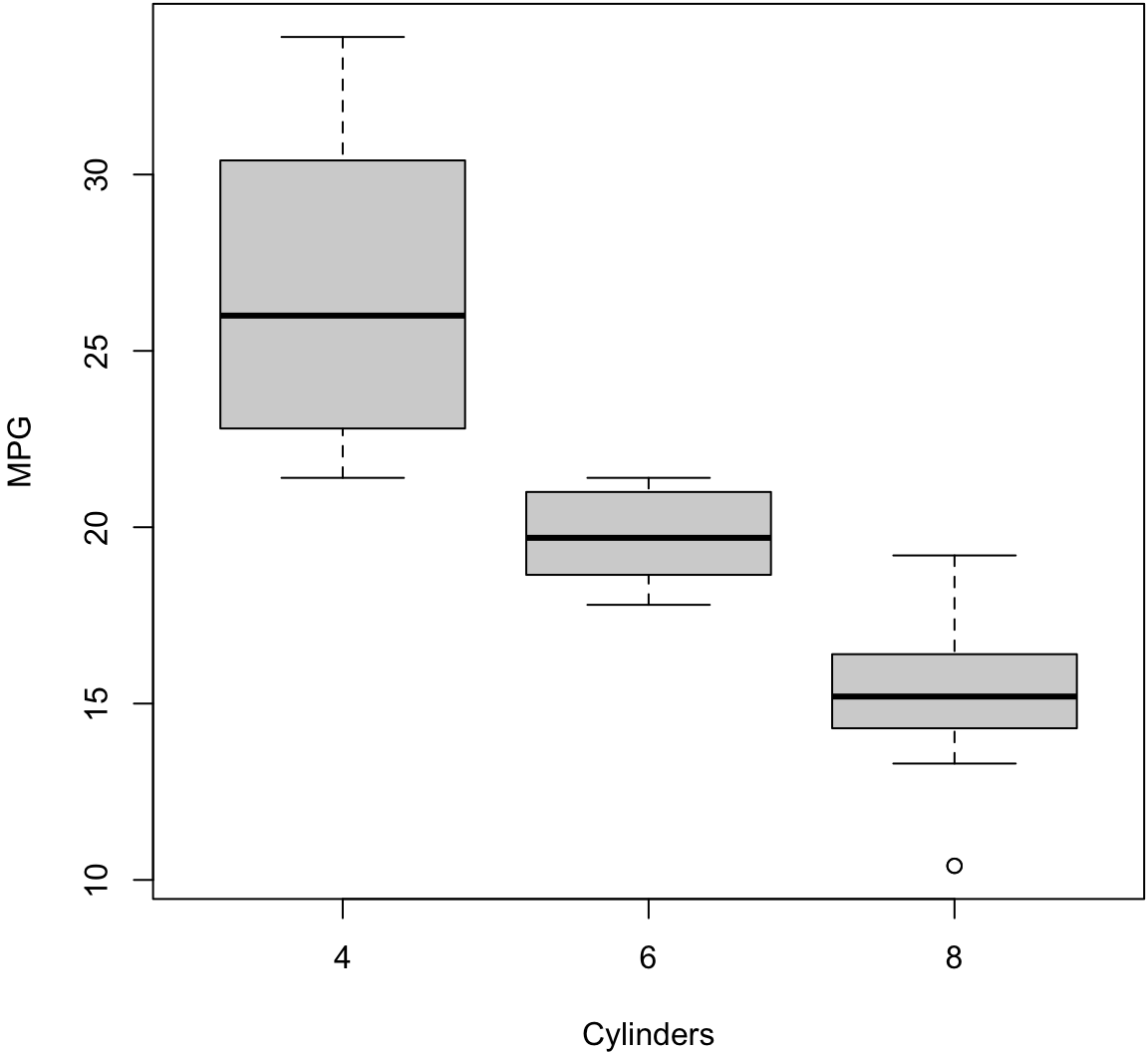
Stacked Barplot
> counts <- table(mtcars$cyl, mtcars$gear)
> counts
3 4 5
4 1 8 2
6 2 4 1
8 12 0 2> barplot(counts, main="Number of Gears and Cylinders",
+ xlab="Gears", col=c("blue","red", "lightgray"))
> legend(x="topright", title="Cyl",
+ legend = rownames(counts),
+ fill = c("blue","red", "lightgray"))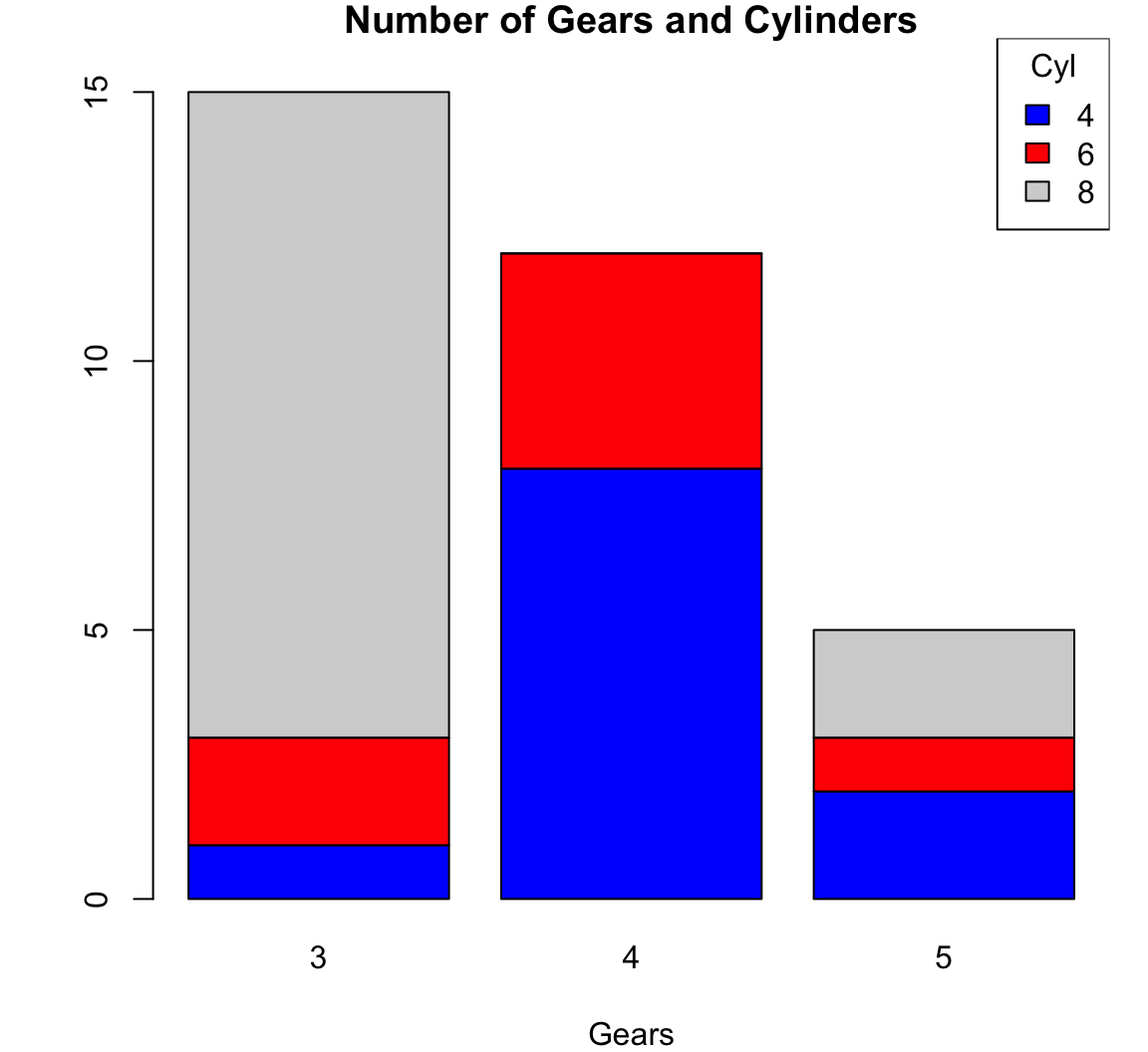
Scatterplot
> plot(mtcars$wt, mtcars$mpg, xlab="Weight (1000 lbs)",
+ ylab="MPG")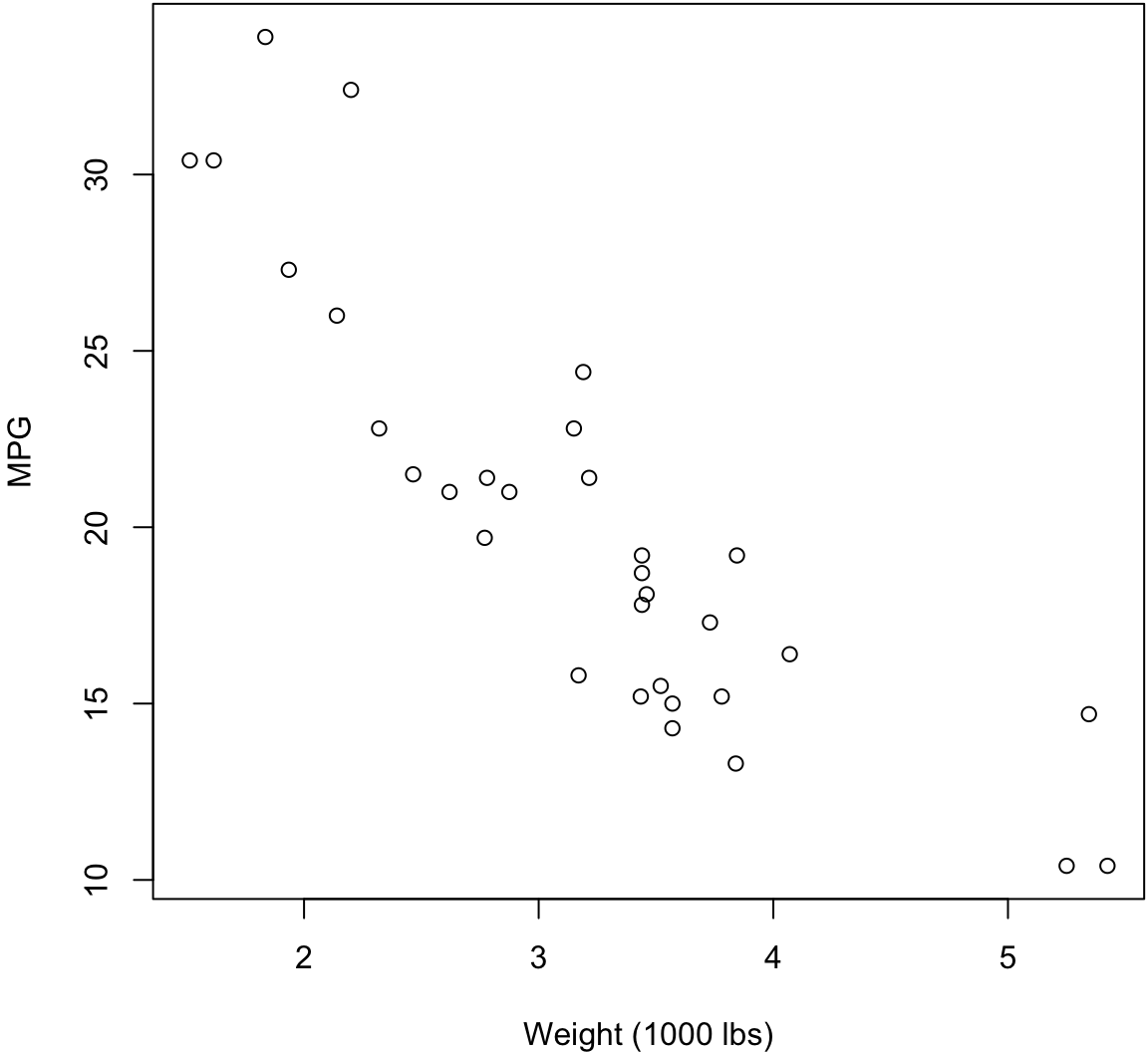
A Grammar of Graphics
Rationale
A grammar for communicating data visualization:
- Data: the data set we are plotting
- Aesthetics: the variation or relationships in the data we want to visualize
- Geometries: the geometric object by which we render the aesthetics
- Coordinates: the coordinate system used (not covered here)
- Facets: the layout of plots required to visualize the data
- Other Options: any other customizations we wish to make, such as changing the color scheme or labels
These are strung together like words in a sentence.
Package ggplot2
The R package ggplot2 implements a grammar of graphics along these lines. First, let’s load ggplot2:
> library(ggplot2)Now let’s set a theme (more on this later):
> theme_set(theme_bw())Pieces of the Grammar
ggplot()aes()geom_*()facet_*()scale_*()theme()labs()
The * is a placeholder for a variety of terms that we will consider.
Geometries
Perhaps the most important aspect of ggplot2 is to understand the “geoms”. We will cover the following:
geom_bar()geom_boxplot()geom_violin()geom_histogram()geom_density()geom_line()geom_point()geom_smooth()geom_hex()
Call Format
The most basic ggplot2 plot is made with something like:
ggplot(data = <DATA FRAME>) +
geom_*(mapping = aes(x = <VAR X>, y = <VAR Y>))where <DATA FRAME> is a data frame and <VAR X> and <VAR Y> are variables (i.e., columns) from this data frame. Recall geom_* is a placeholder for a geometry such as geom_boxplot.
Layers
There’s a complex “layers” construct occurring in the ggplot2 package. However, for our purposes, it suffices to note that the different parts of the plots are layered together through the + operator:
> ggplot(data = mpg) +
+ geom_point(mapping = aes(x = displ, y = hwy, color=drv)) +
+ geom_smooth(mapping = aes(x = displ, y = hwy, color=drv)) +
+ scale_color_brewer(palette = "Set1", name = "Drivetrain") +
+ labs(title = "Highway MPG By Drivetrain and Displacement",
+ x = "Displacement", y = "Highway MPG")Placement of the aes() Call
In the previous slide, we saw that the same aes() call was made for two geom’s. When this is the case, we may more simply call aes() from within ggplot():
> ggplot(data = mpg, mapping = aes(x = displ, y = hwy, color=drv)) +
+ geom_point() +
+ geom_smooth() +
+ scale_color_brewer(palette = "Set1", name = "Drivetrain") +
+ labs(title = "Highway MPG By Drivetrain and Displacement",
+ x = "Displacement", y = "Highway MPG")There may be cases where different geom’s are layered and require different aes() calls. This is something to keep in mind as we go through the specifics of the ggplot2 package.
Original Publications
Wickham, H. (2010) A Layered Grammar of Graphics. Journal of Computational and Graphical Statistics, 19 (1): 3–28.
This paper designs an implementation of The Grammar of Graphics by Leland Wilkinson (published in 2005).
Documentation
- In R:
help(package="ggplot2") - http://docs.ggplot2.org/current/
- http://www.cookbook-r.com/Graphs/
- ggplot2: Elegant Graphics for Data Analysis (somewhat outdated, but gives clear rationale)
Barplots
The geom_bar() layer forms a barplot and only requires an x assignment in the aes() call:
> ggplot(data = diamonds) +
+ geom_bar(mapping = aes(x = cut))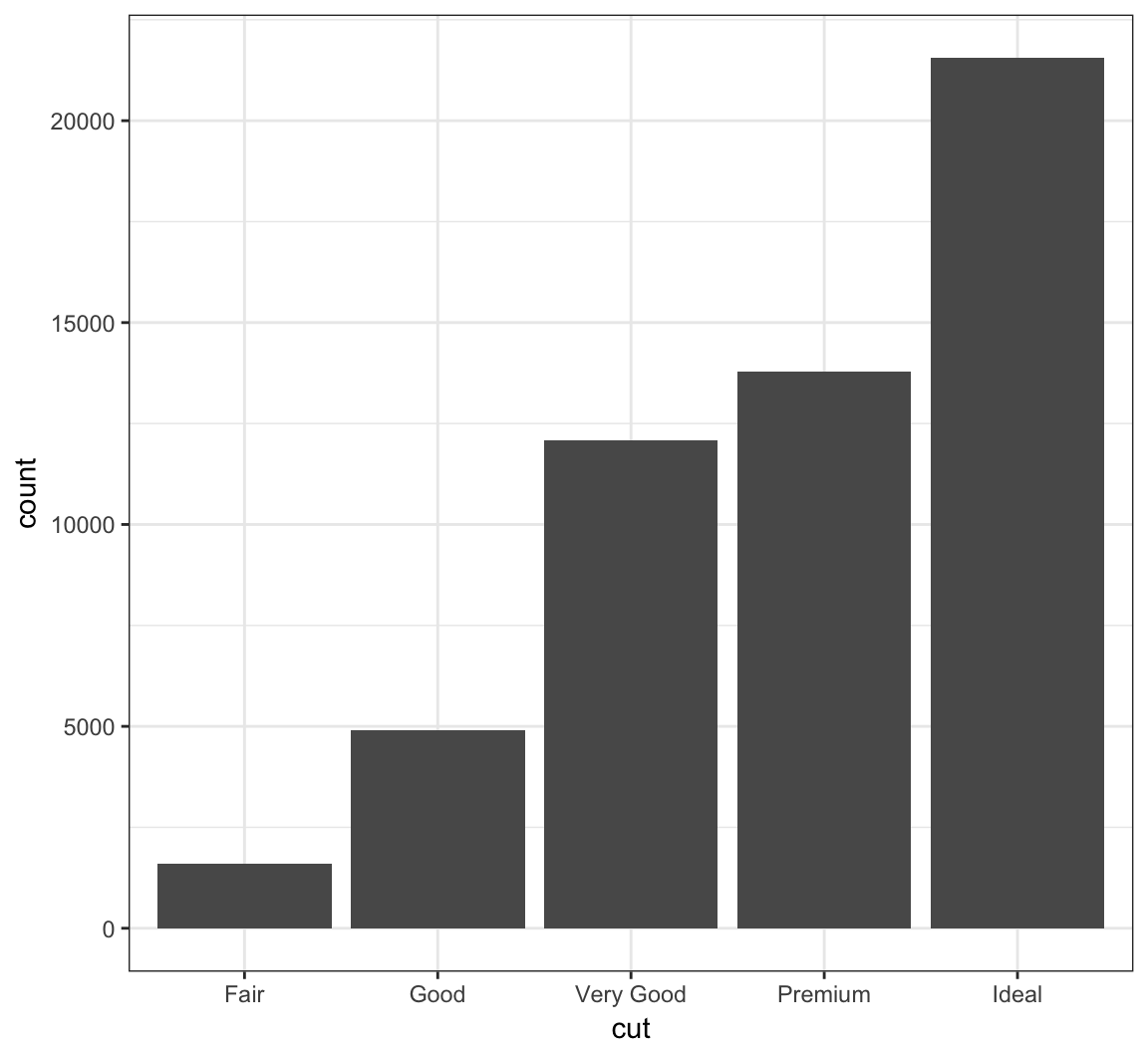
Color in the bars by assigning fill in geom_bar(), but outside of aes():
> ggplot(data = diamonds) +
+ geom_bar(mapping = aes(x = cut), fill = "tomato")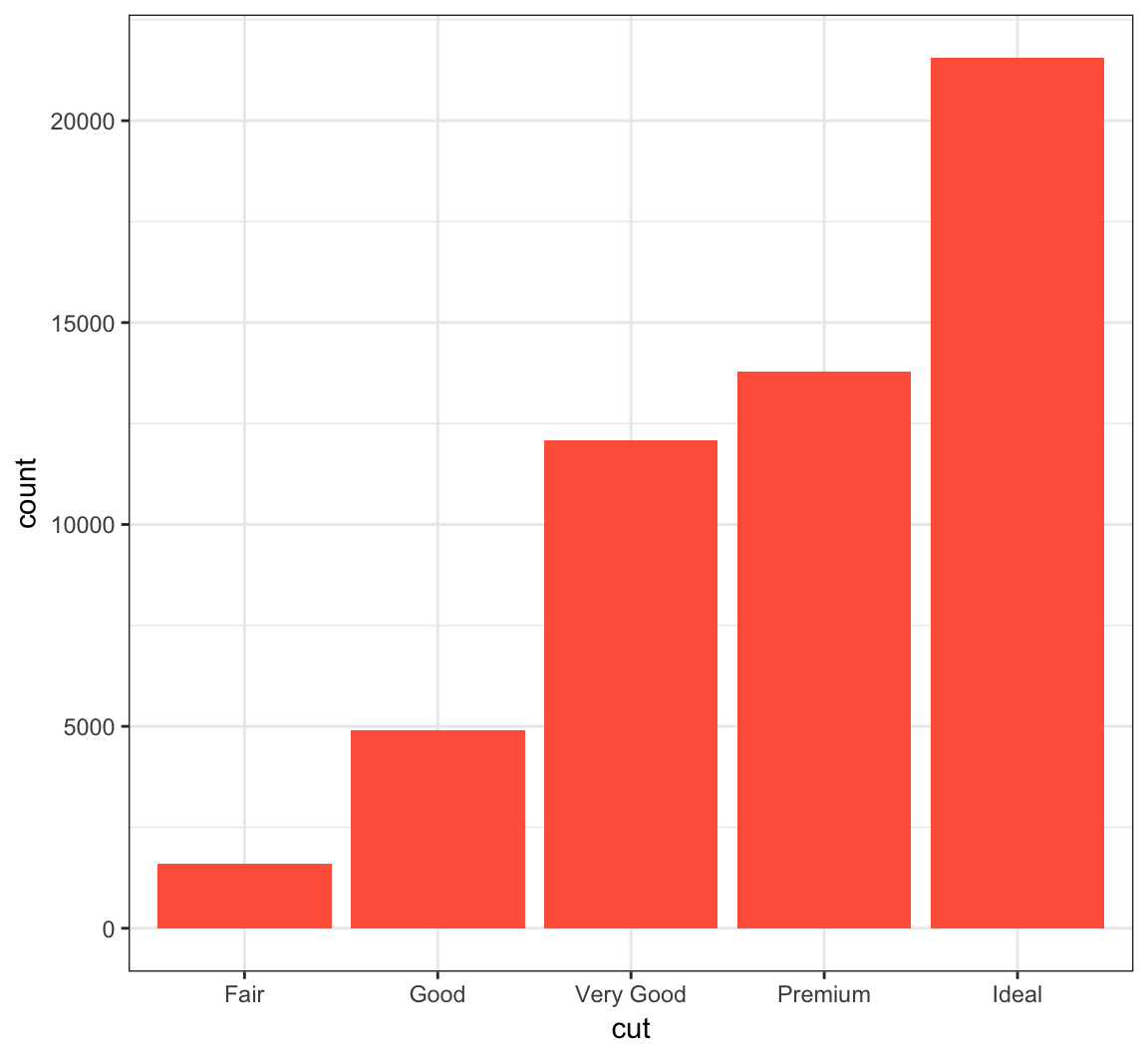
Color within the bars according to a variable by assigning fill in geom_bar() inside of aes():
> ggplot(data = diamonds) +
+ geom_bar(mapping = aes(x = cut, fill = cut))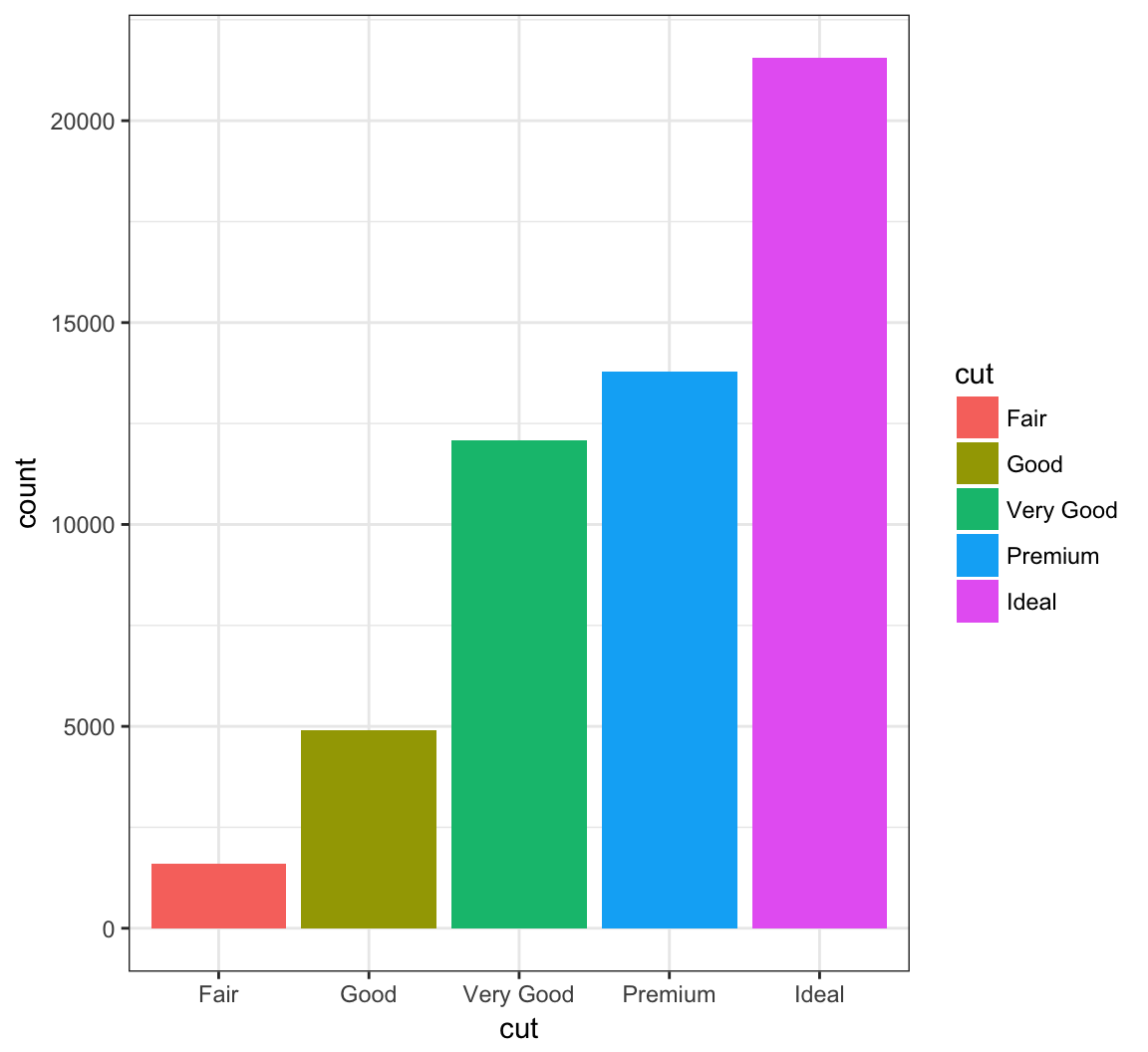
When we use fill = clarity within aes(), we see that it shows the proportion of each clarity value within each cut value:
> ggplot(data = diamonds) +
+ geom_bar(mapping = aes(x = cut, fill = clarity))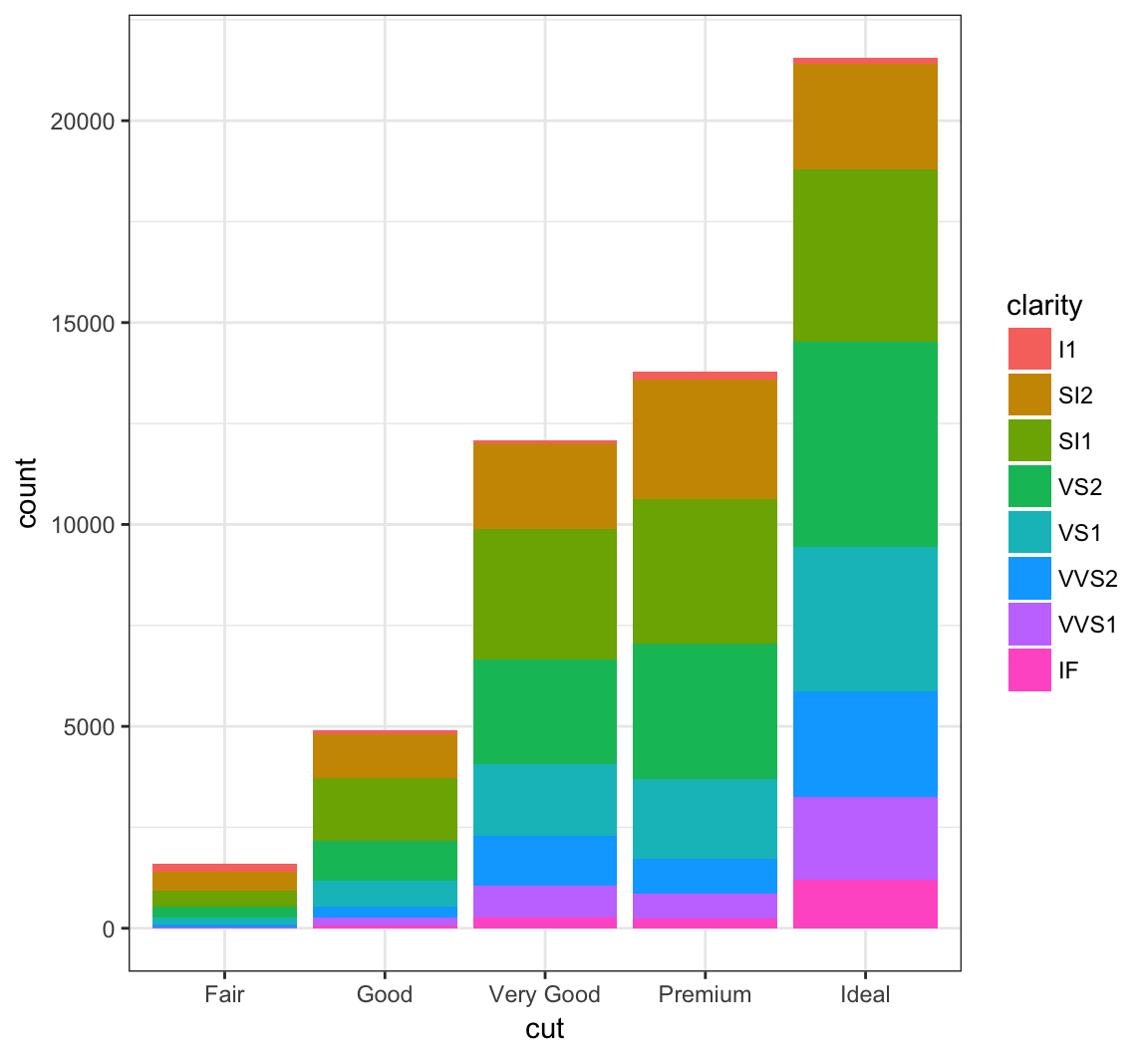
By setting position = "dodge" outside of aes(), it shows bar charts for the clarity values within each cut value:
> ggplot(data = diamonds) +
+ geom_bar(mapping= aes(x = cut, fill = clarity),
+ position = "dodge")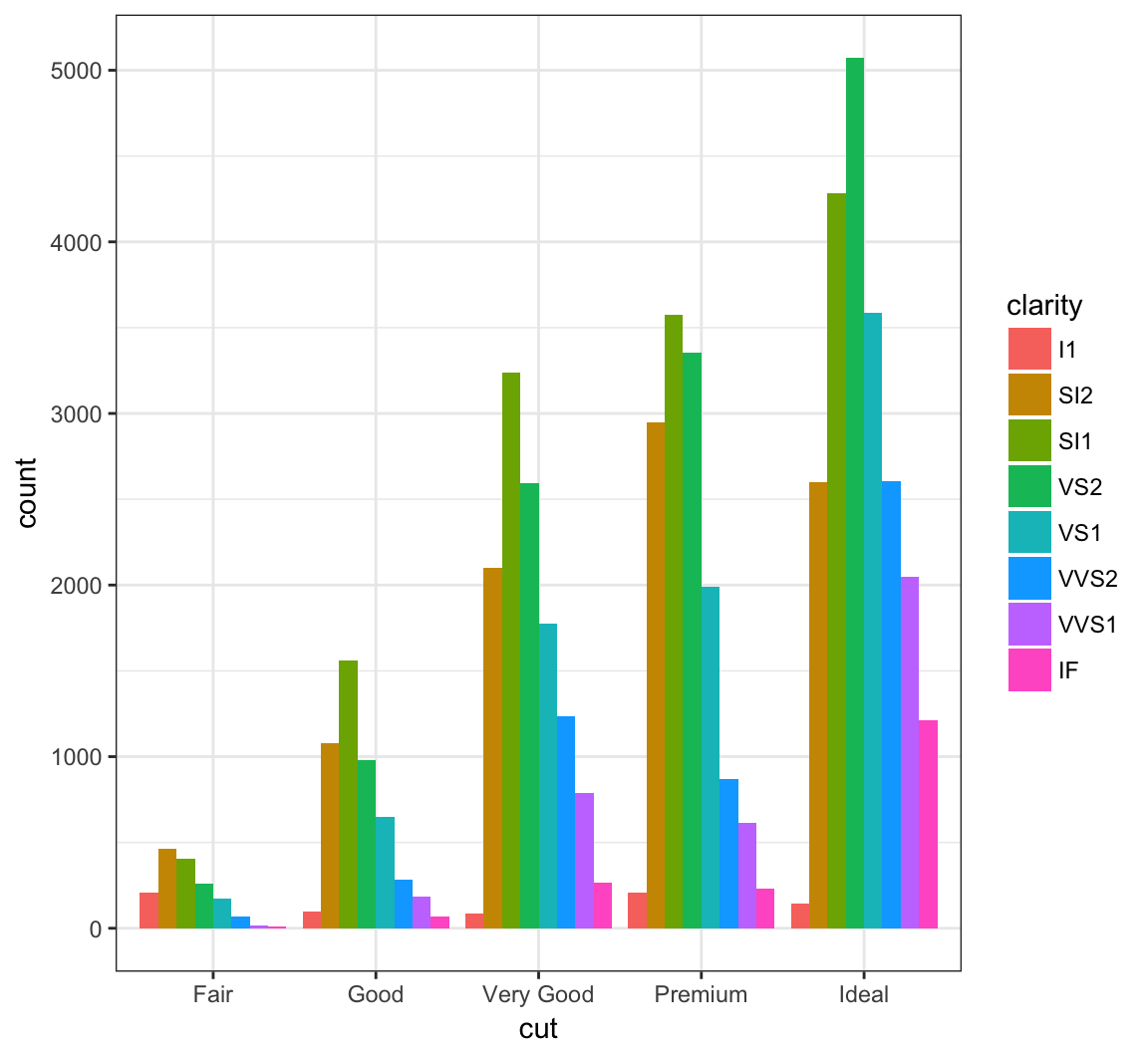
By setting position = "fill", it shows the proportion of clarity values within each cut value and no longer shows the cut values:
> ggplot(data = diamonds) +
+ geom_bar(mapping=aes(x = cut, fill = clarity),
+ position = "fill") +
+ labs(x = "cut", y = "relative proporition within cut")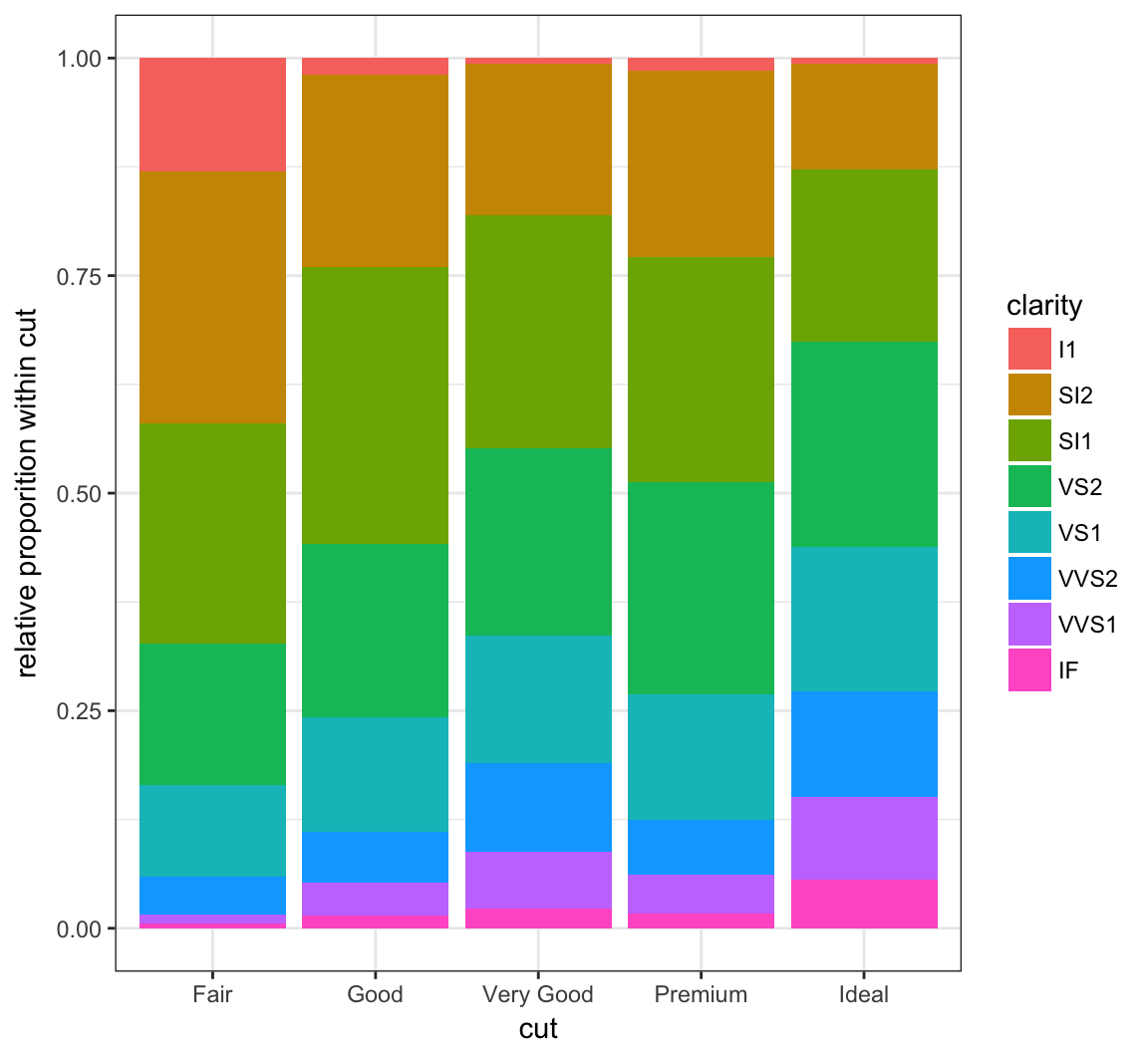
Boxplots and Violin Plots
The geom_boxplot() layer forms a boxplot and requires both x and y assignments in the aes() call, even when plotting a single boxplot:
> ggplot(data = mpg) +
+ geom_boxplot(mapping = aes(x = 1, y = hwy))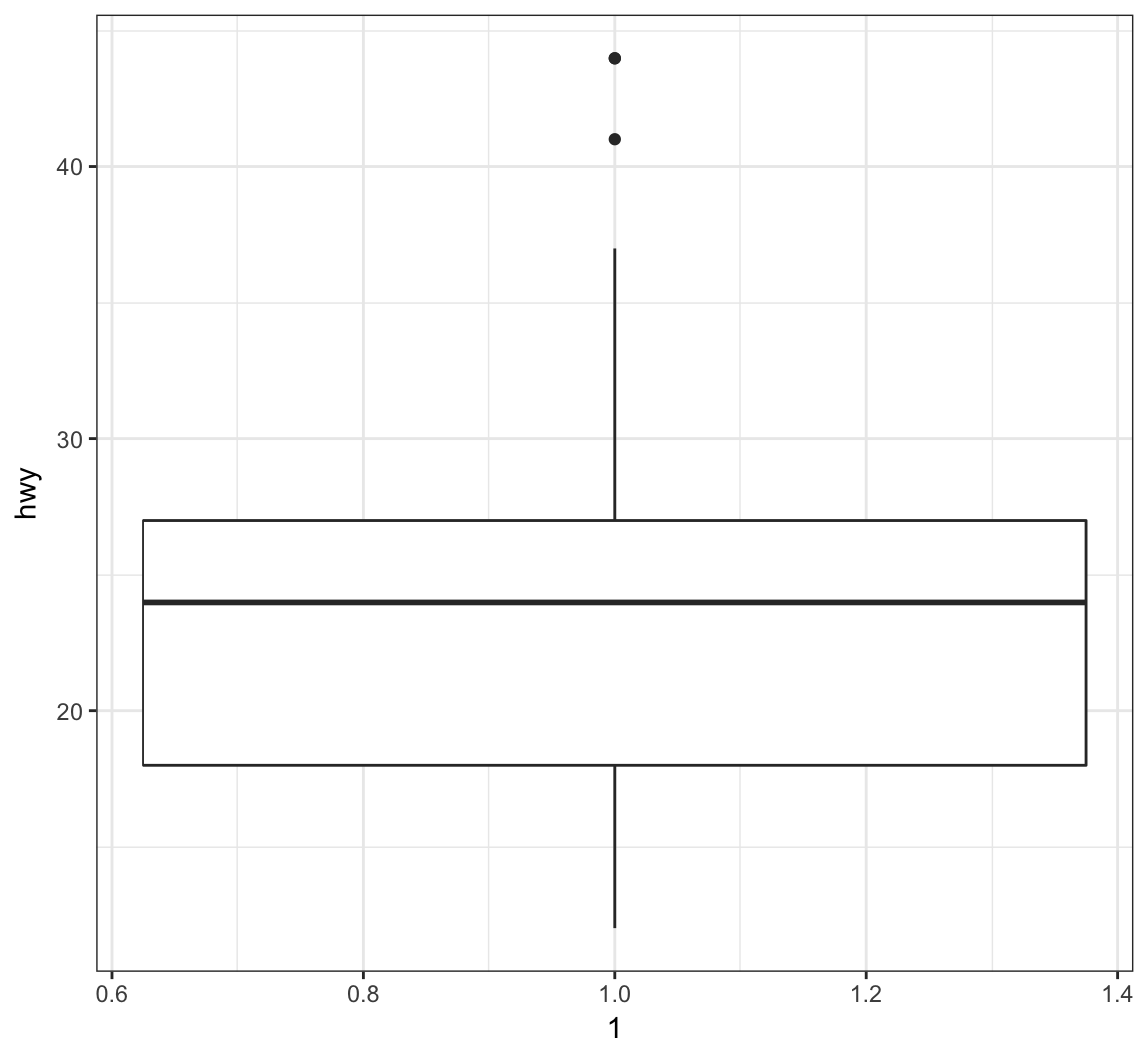
Color in the boxes by assigning fill in geom_boxplot(), but outside of aes():
> ggplot(data = mpg) +
+ geom_boxplot(mapping = aes(x = 1, y = hwy),
+ fill="lightblue") +
+ labs(x=NULL)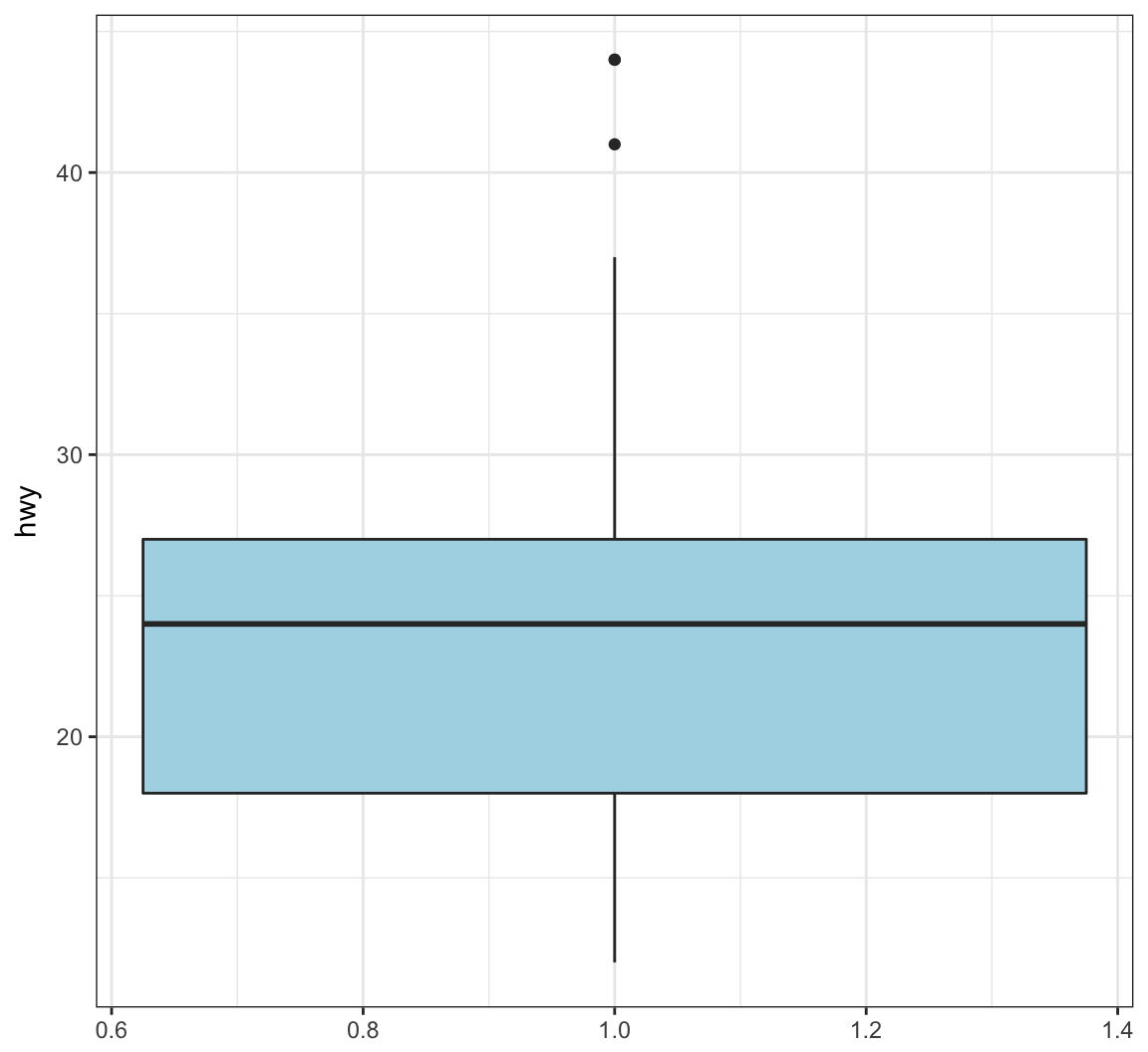
Show a boxplot for the y values occurring within each x factor level by making these assignments in aes():
> ggplot(data = mpg) +
+ geom_boxplot(mapping = aes(x = factor(cyl), y = hwy))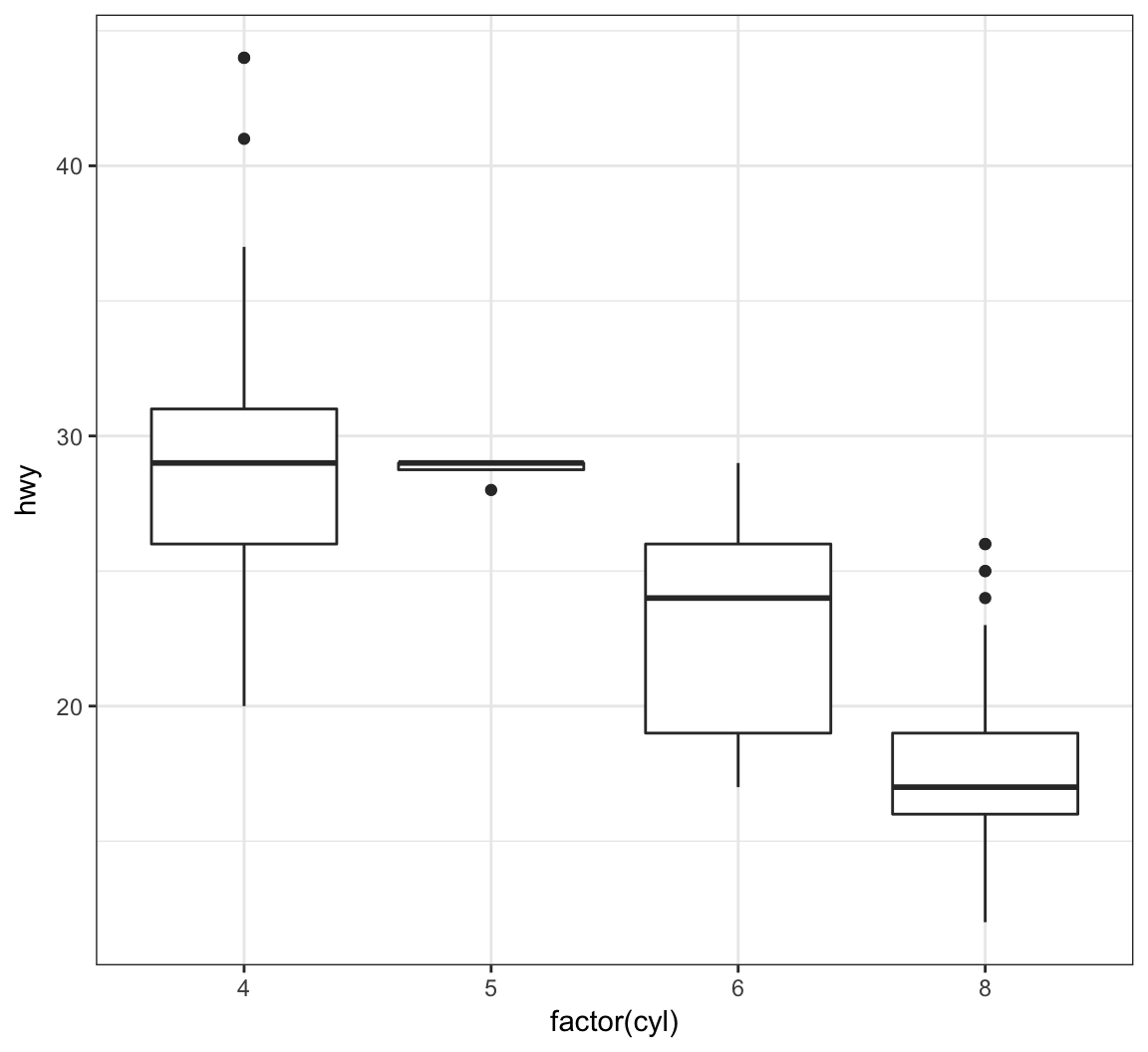
By assigning the fill argument within aes(), we can color each boxplot according to the x-axis factor variable:
> ggplot(data = mpg) +
+ geom_boxplot(mapping = aes(x = factor(cyl), y = hwy,
+ fill = factor(cyl)))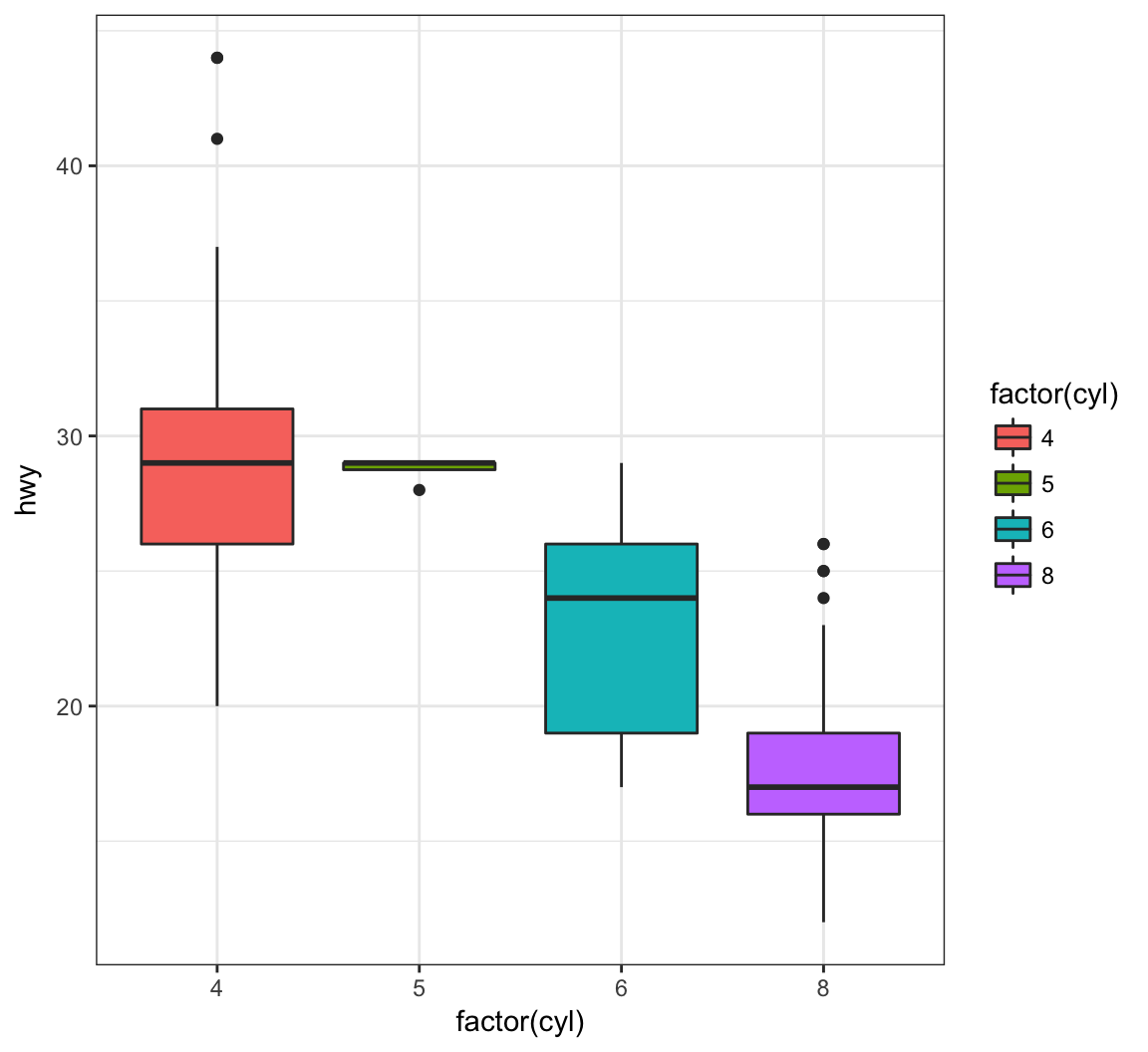
The geom_jitter() function plots the data points and randomly jitters them so we can better see all of the points:
> ggplot(data = mpg, mapping = aes(x=factor(cyl), y=hwy)) +
+ geom_boxplot(fill = "lightblue") +
+ geom_jitter(width = 0.2)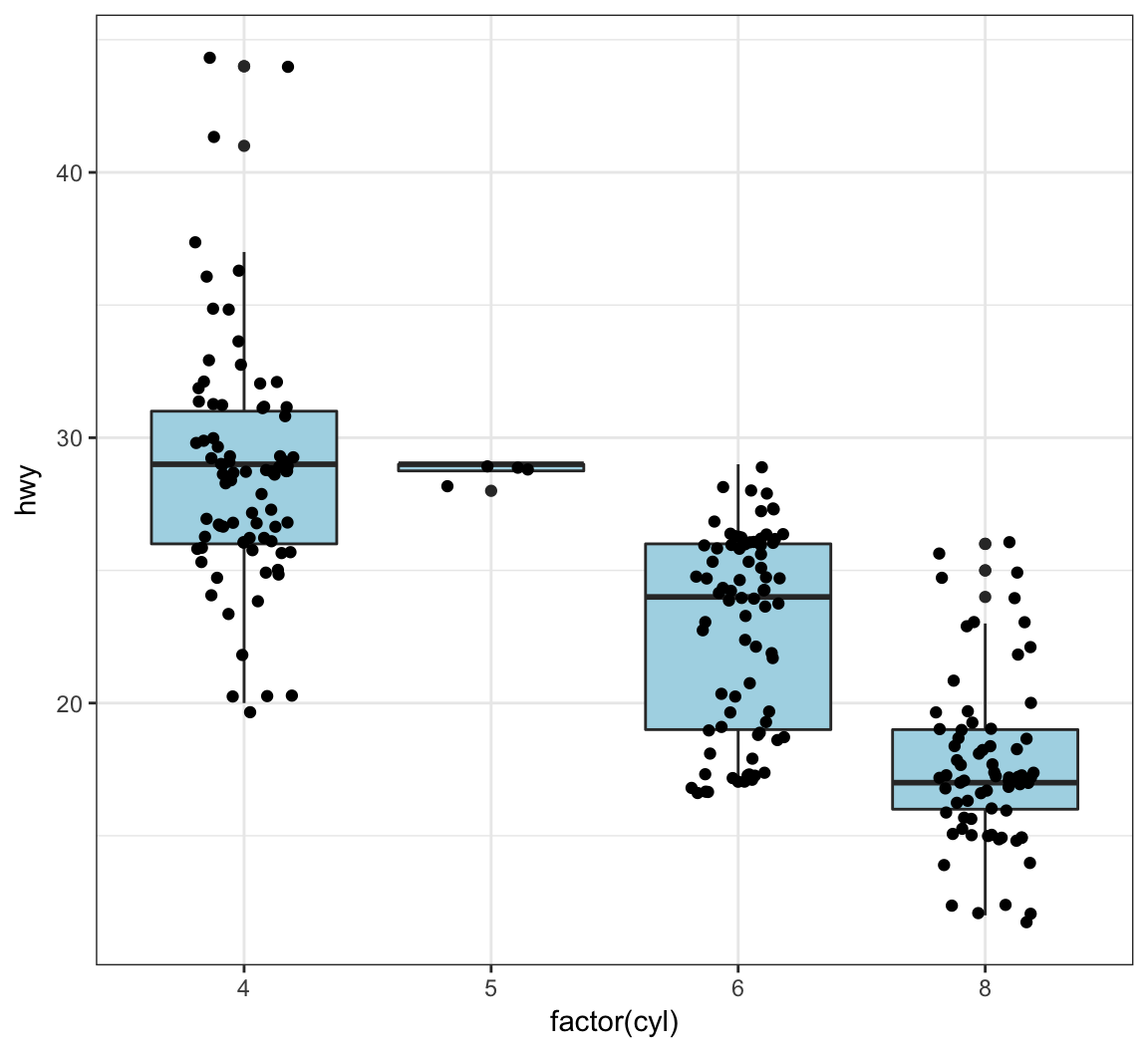
A violin plot, called via geom_violin(), is similar to a boxplot, except shows a density plot turned on its side and reflected across its vertical axis:
> ggplot(data = mpg) +
+ geom_violin(mapping = aes(x = drv, y = hwy))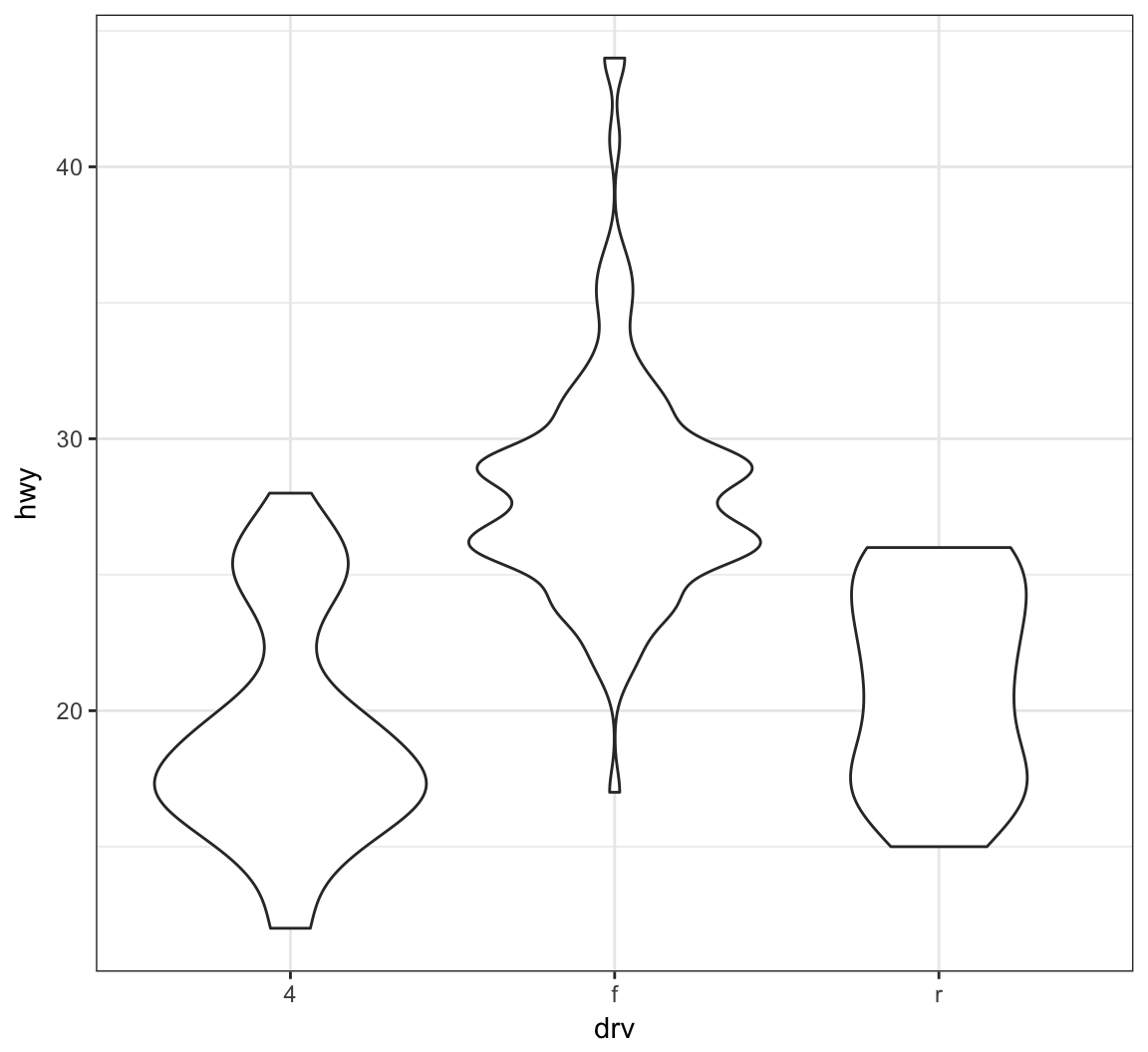
Add a geom_jitter() to see how the original data points relate to the violin plots:
> ggplot(data = mpg, mapping = aes(x = drv, y = hwy)) +
+ geom_violin(adjust=1.2) +
+ geom_jitter(width=0.2, alpha=0.5)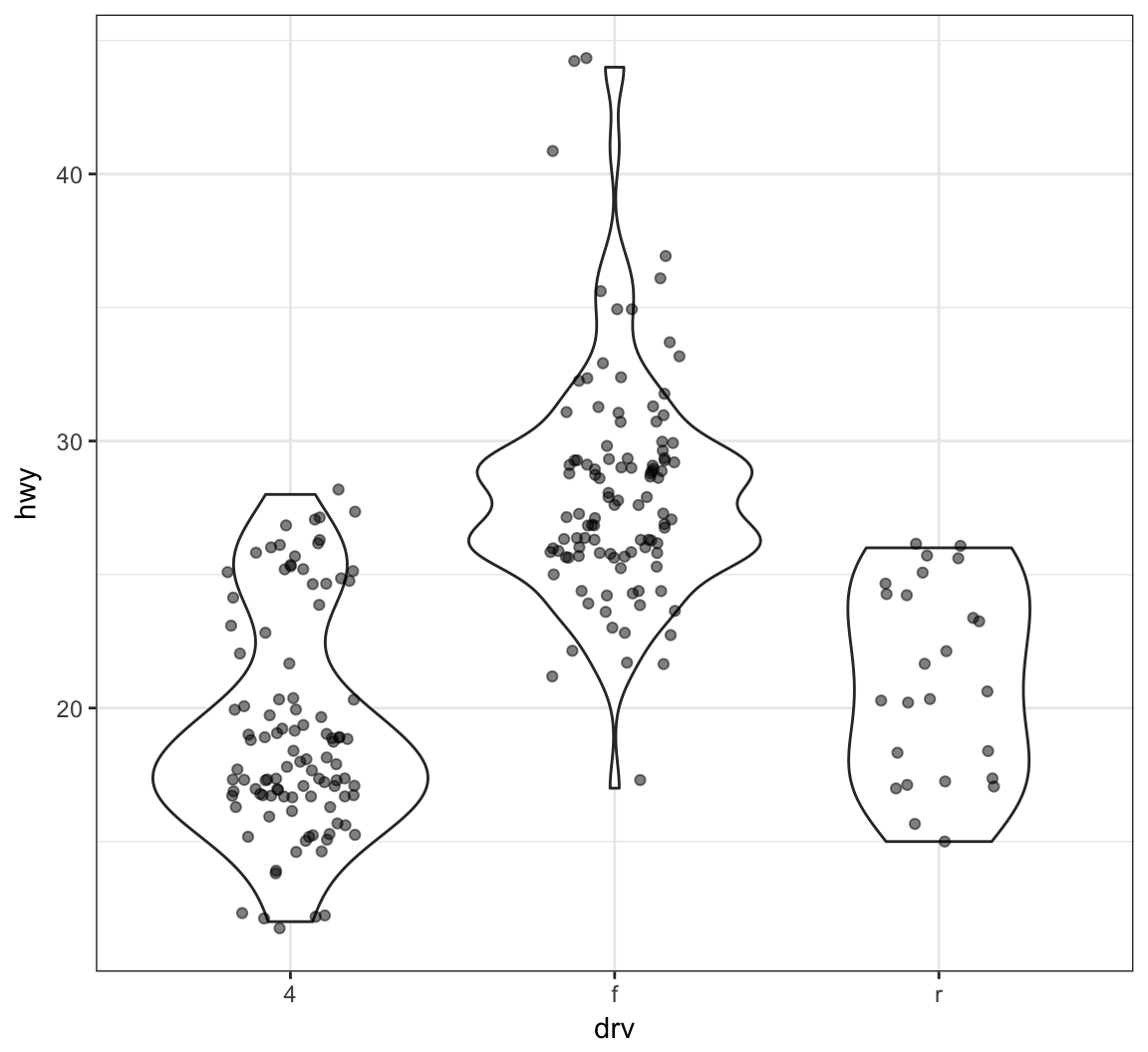
Boxplot example on the gapminder data:
> ggplot(gapminder, aes(x = continent, y = lifeExp)) +
+ geom_boxplot(outlier.colour = "red") +
+ geom_jitter(width = 0.1, alpha = 0.25)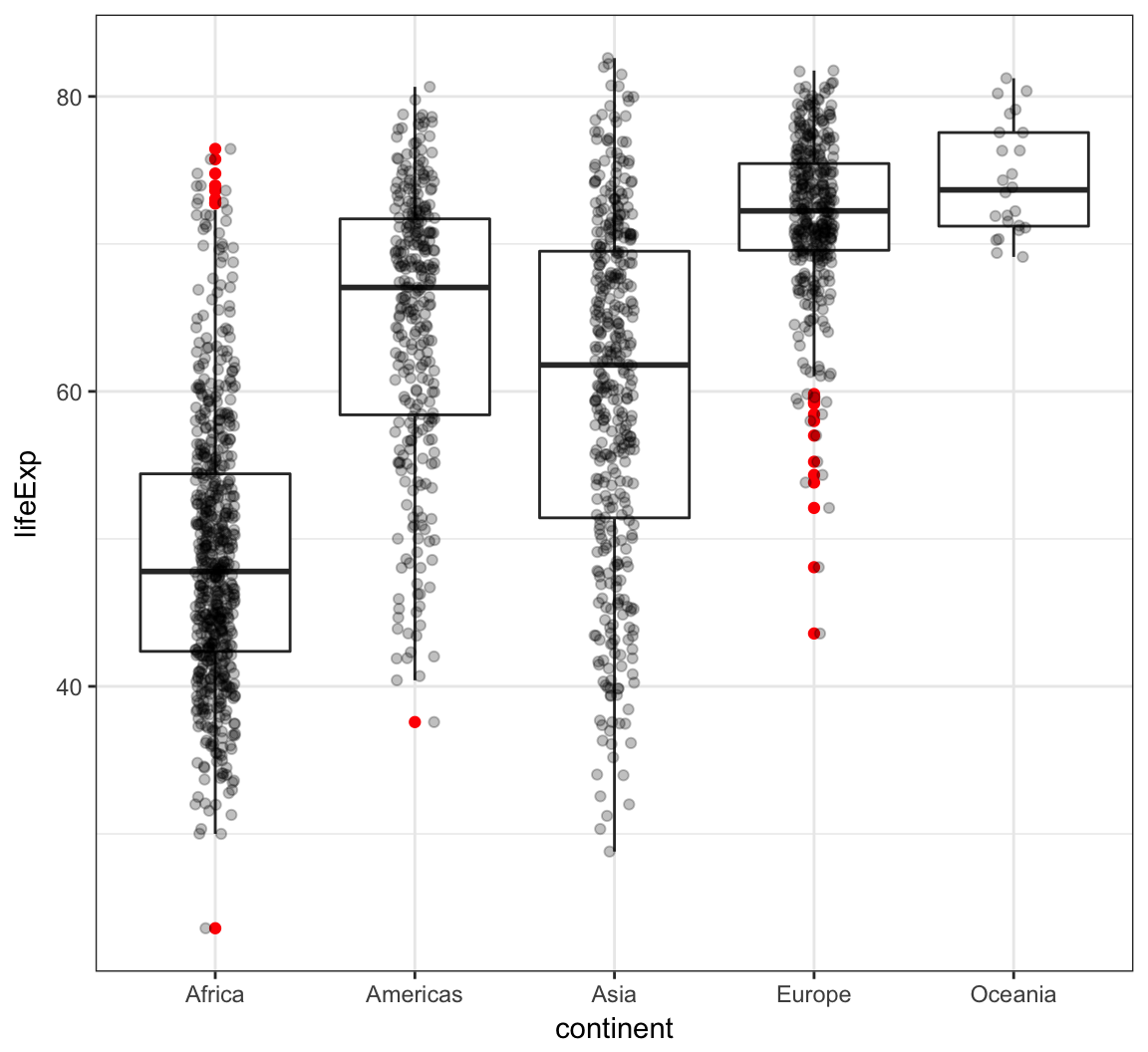
Analogous violin plot example on the gapminder data:
> ggplot(gapminder, aes(x = continent, y = lifeExp)) +
+ geom_violin() +
+ geom_jitter(width = 0.1, alpha = 0.25)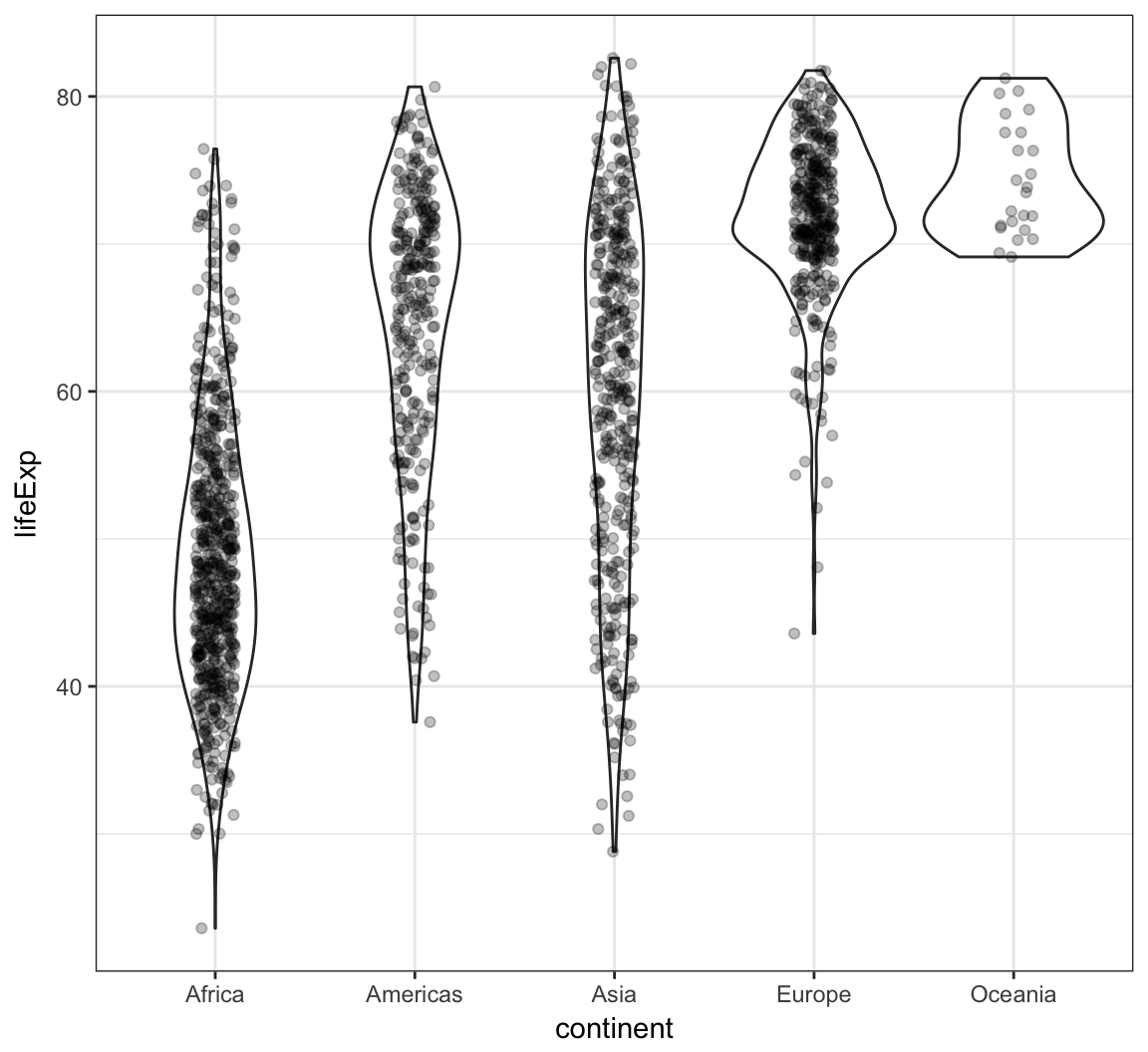
Histograms and Density Plots
We can create a histogram using the geom_histogram() layer, which requires an x argument only in the aes() call:
> ggplot(gapminder) +
+ geom_histogram(mapping = aes(x=lifeExp))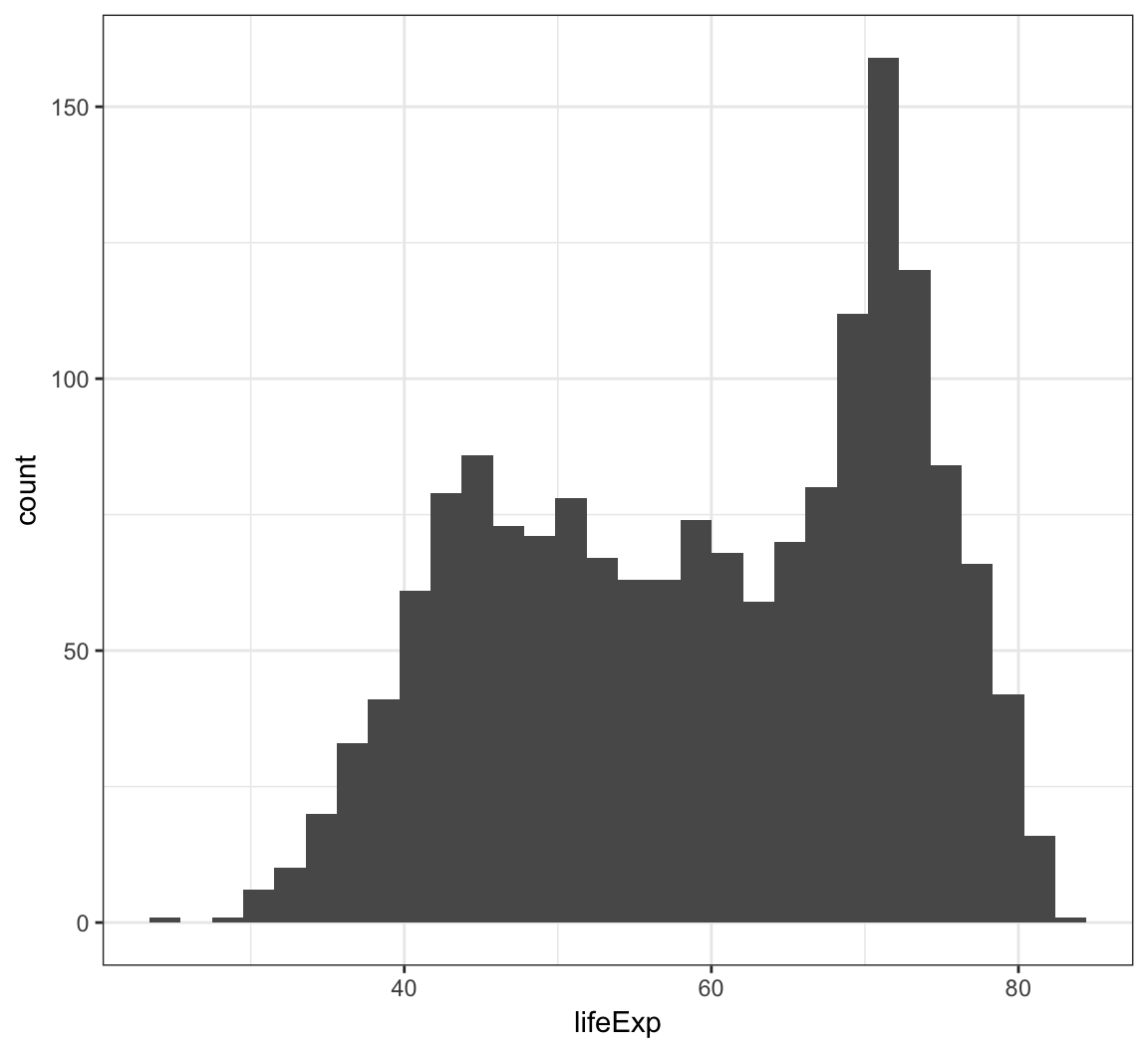
We can change the bin width directly in the histogram, which is an intuitive parameter to change based on visual inspection:
> ggplot(gapminder) +
+ geom_histogram(mapping = aes(x=lifeExp), binwidth=5)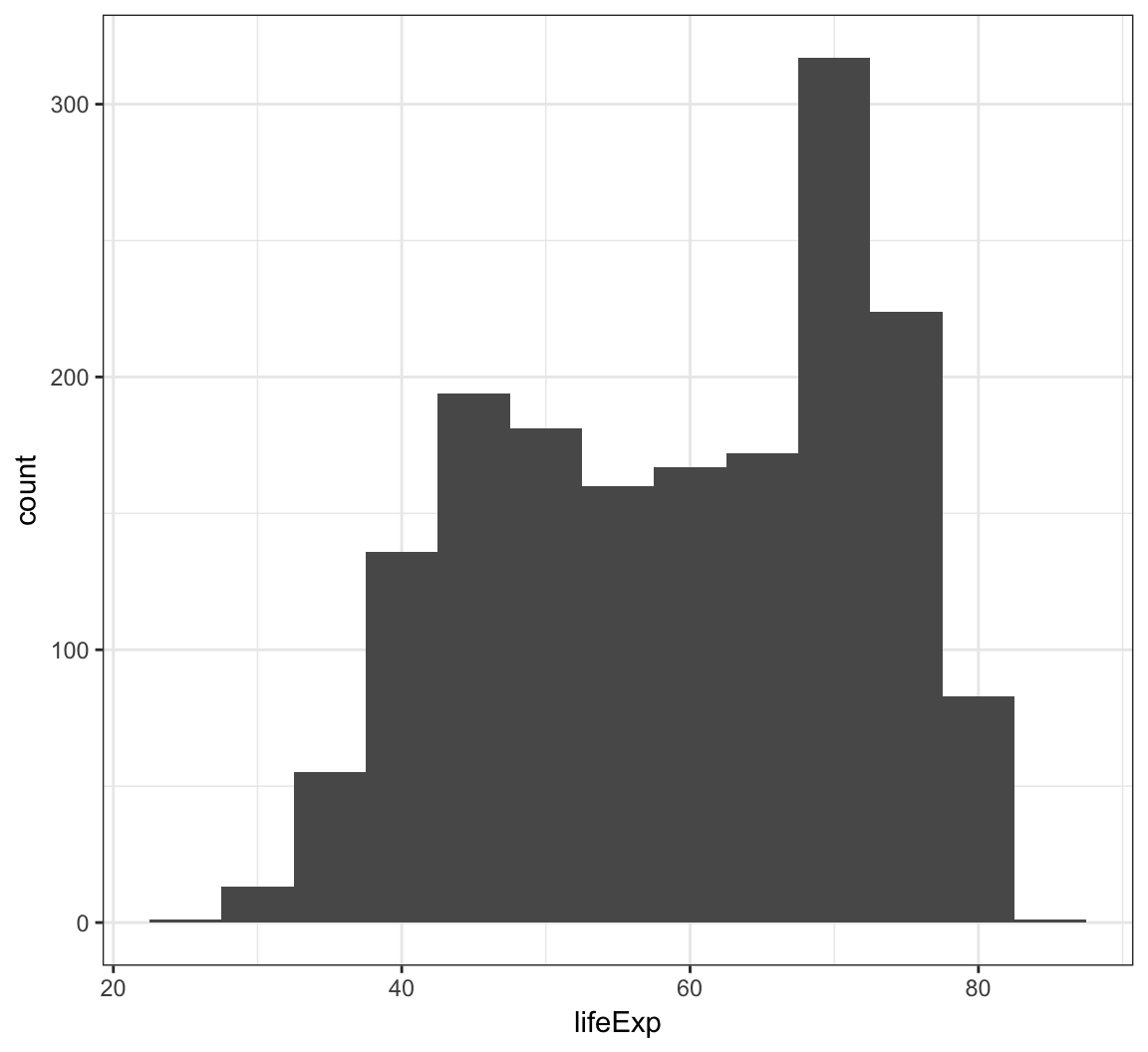
The bins are sometimes centered in an unexpected manner in ggplot2:
> ggplot(diamonds) +
+ geom_histogram(mapping = aes(x=price), binwidth = 1000)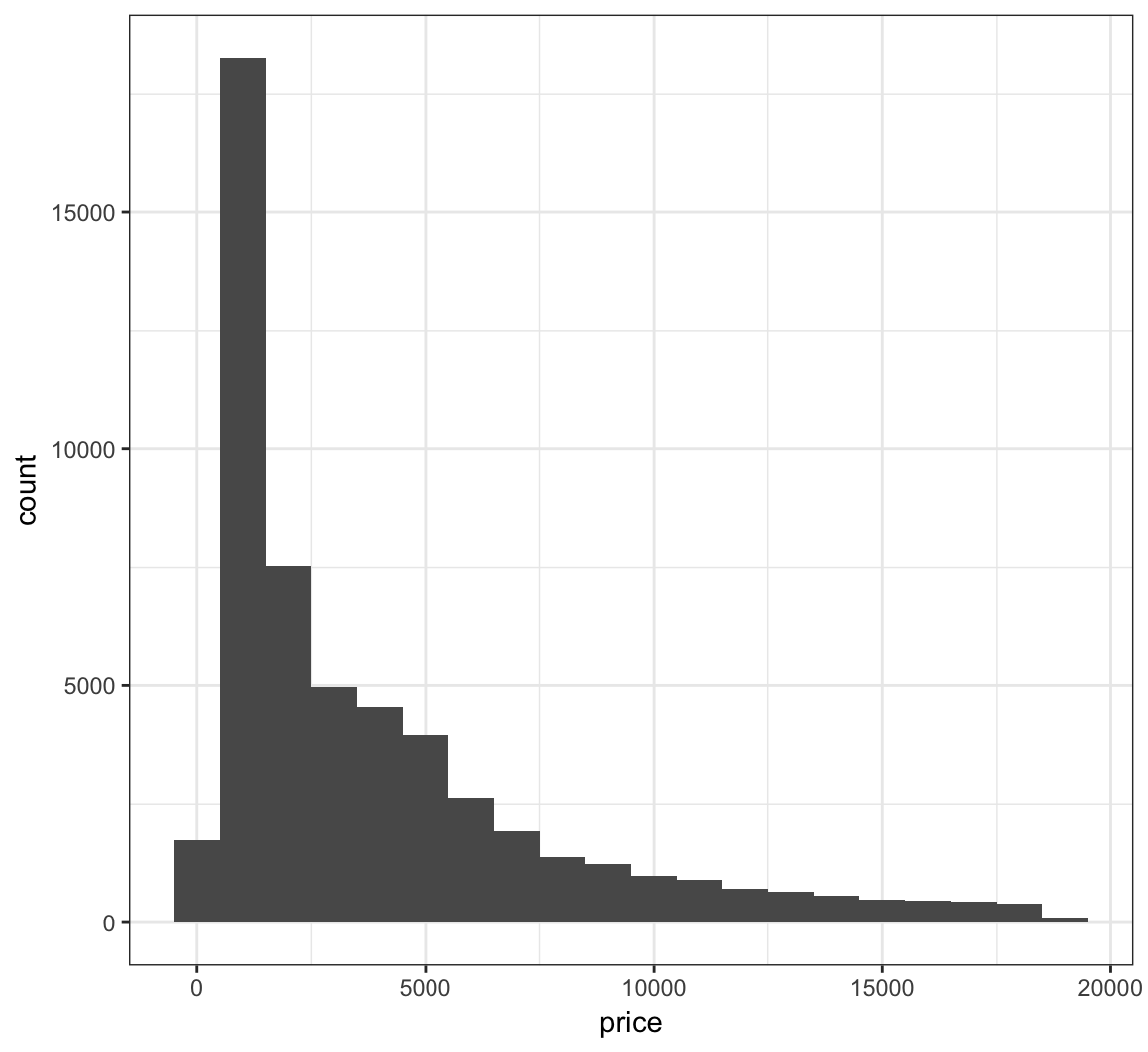
Let’s fix how the bins are centered (make center half of binwidth).
> ggplot(diamonds) +
+ geom_histogram(mapping = aes(x=price), binwidth = 1000,
+ center=500)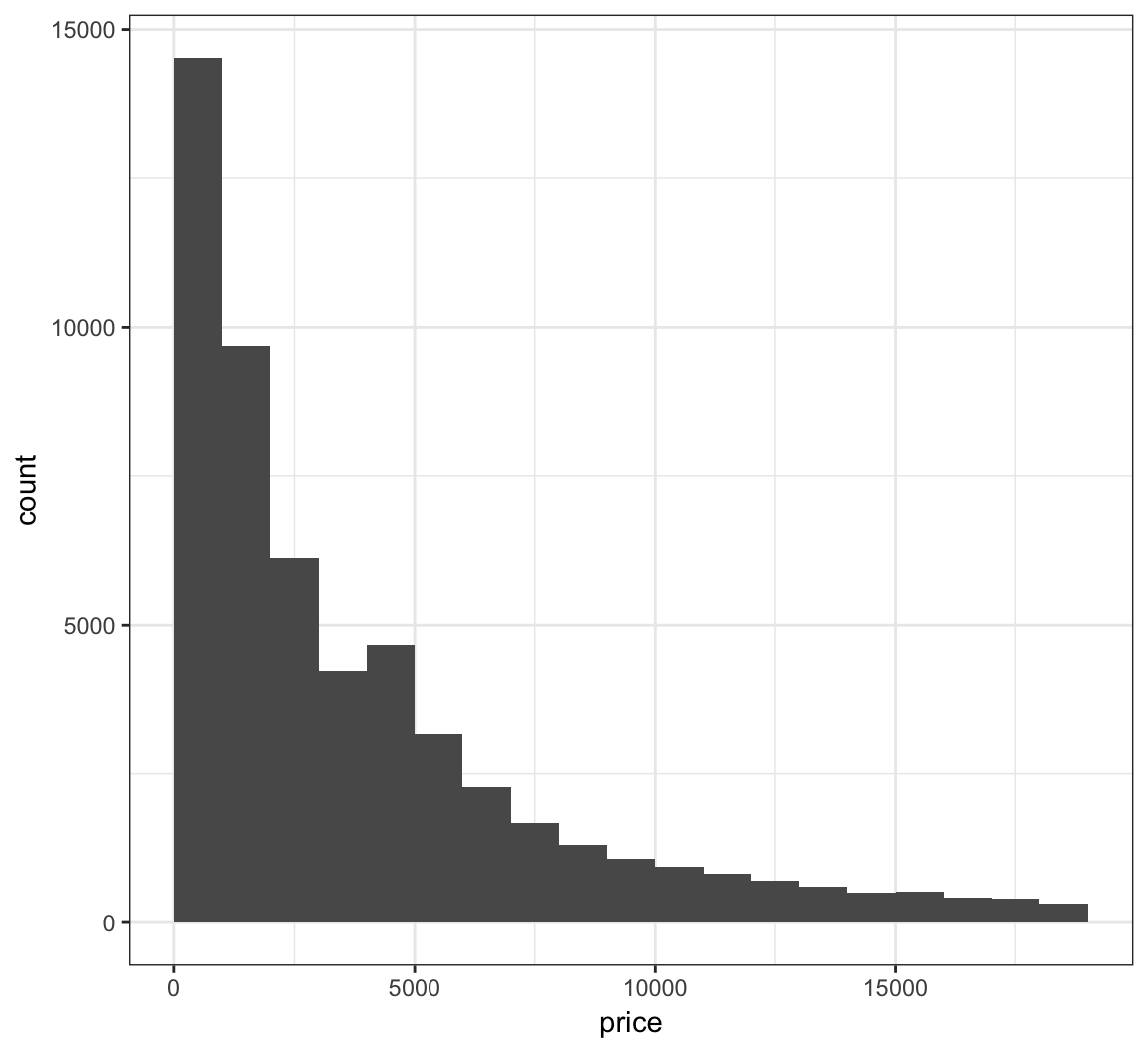
Instead of counts on the y-axis, we may instead want the area of the bars to sum to 1, like a probability density:
> ggplot(gapminder) +
+ geom_histogram(mapping = aes(x=lifeExp, y=..density..),
+ binwidth=5)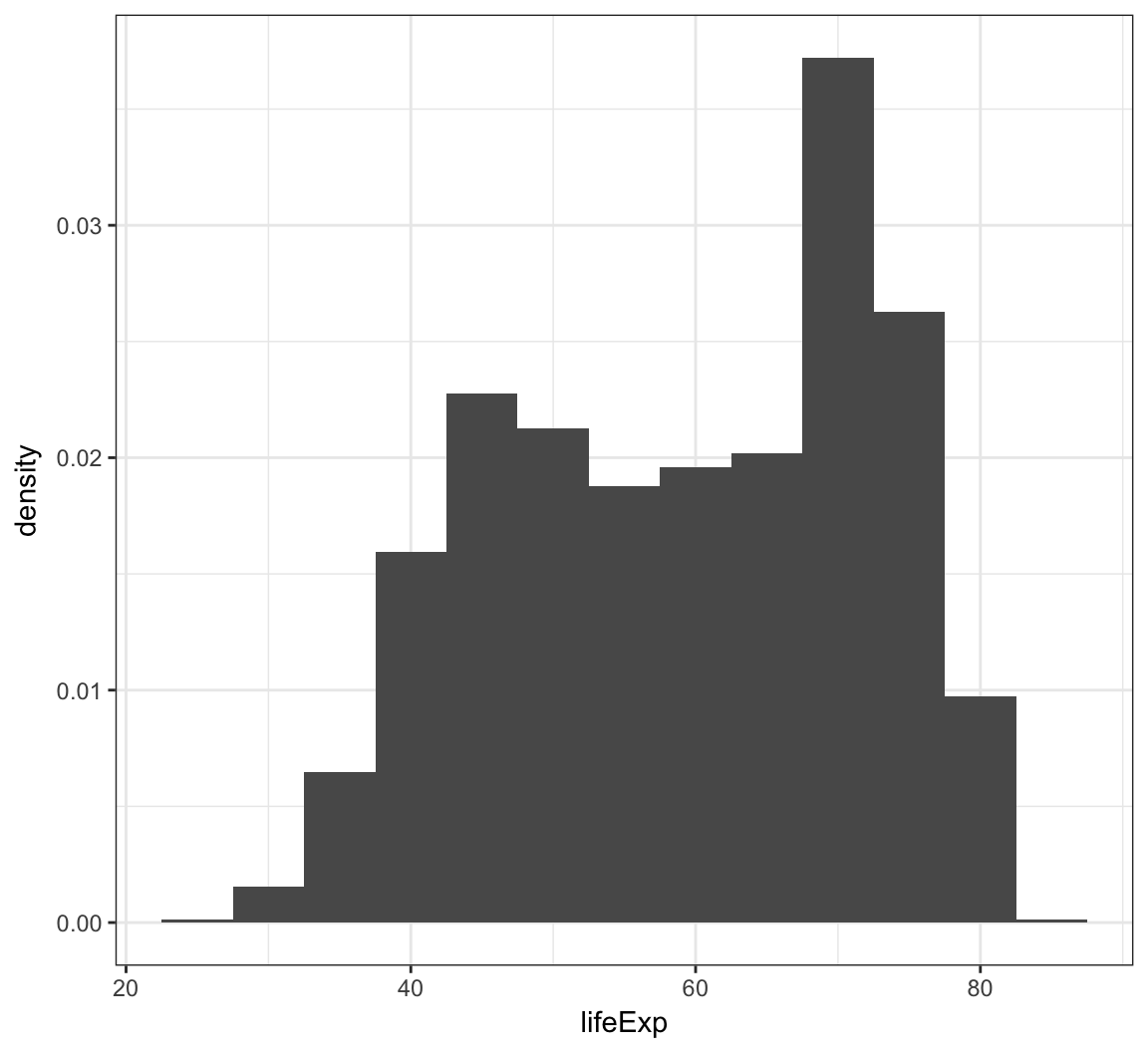
When we use fill = continent within aes(), we see that it shows the counts of each continent value within each lifeExp bin:
> ggplot(gapminder) +
+ geom_histogram(mapping = aes(x=lifeExp, fill = continent),
+ binwidth = 5)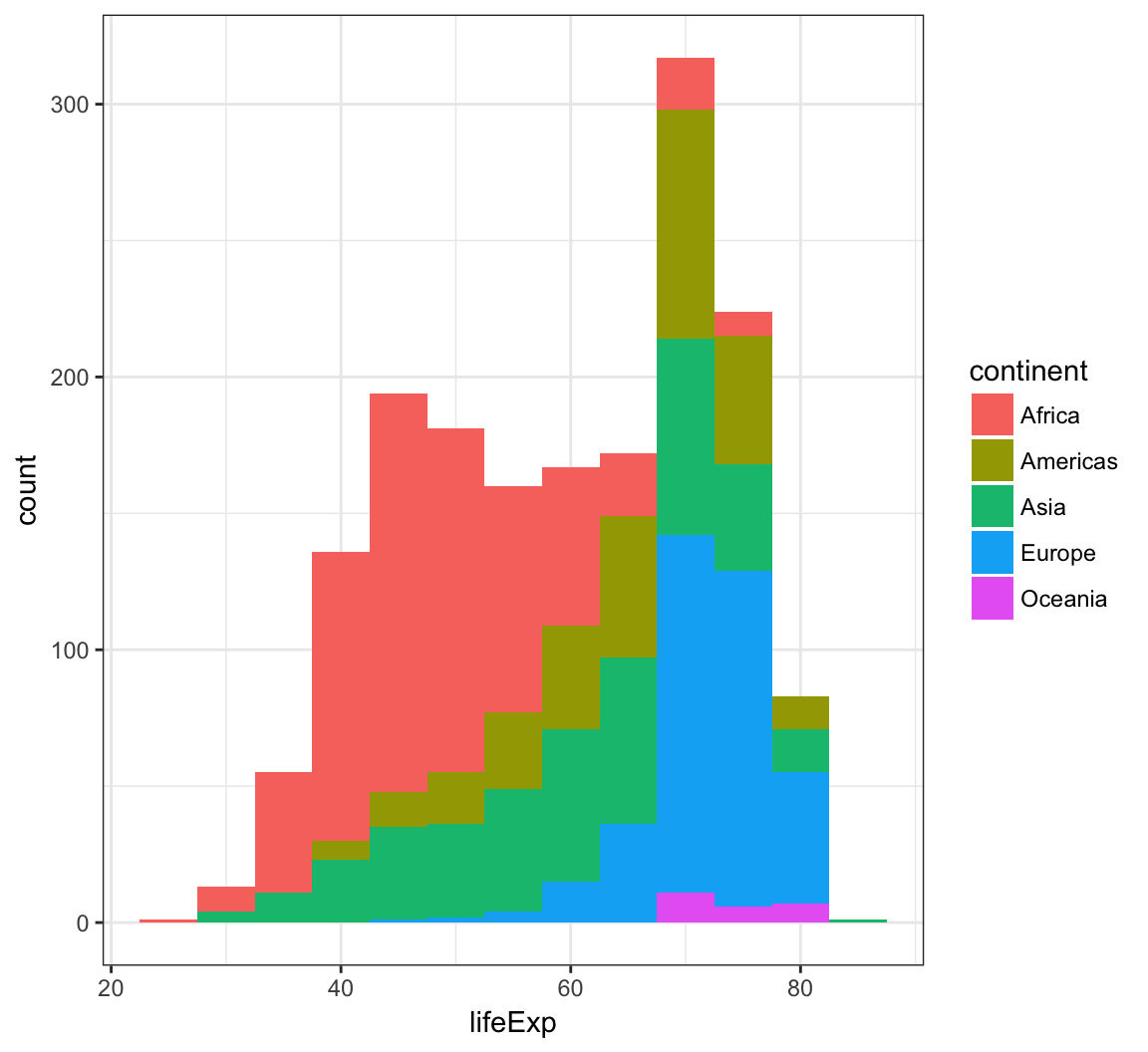
Display a density plot using the geom_density() layer:
> ggplot(gapminder) +
+ geom_density(mapping = aes(x=lifeExp))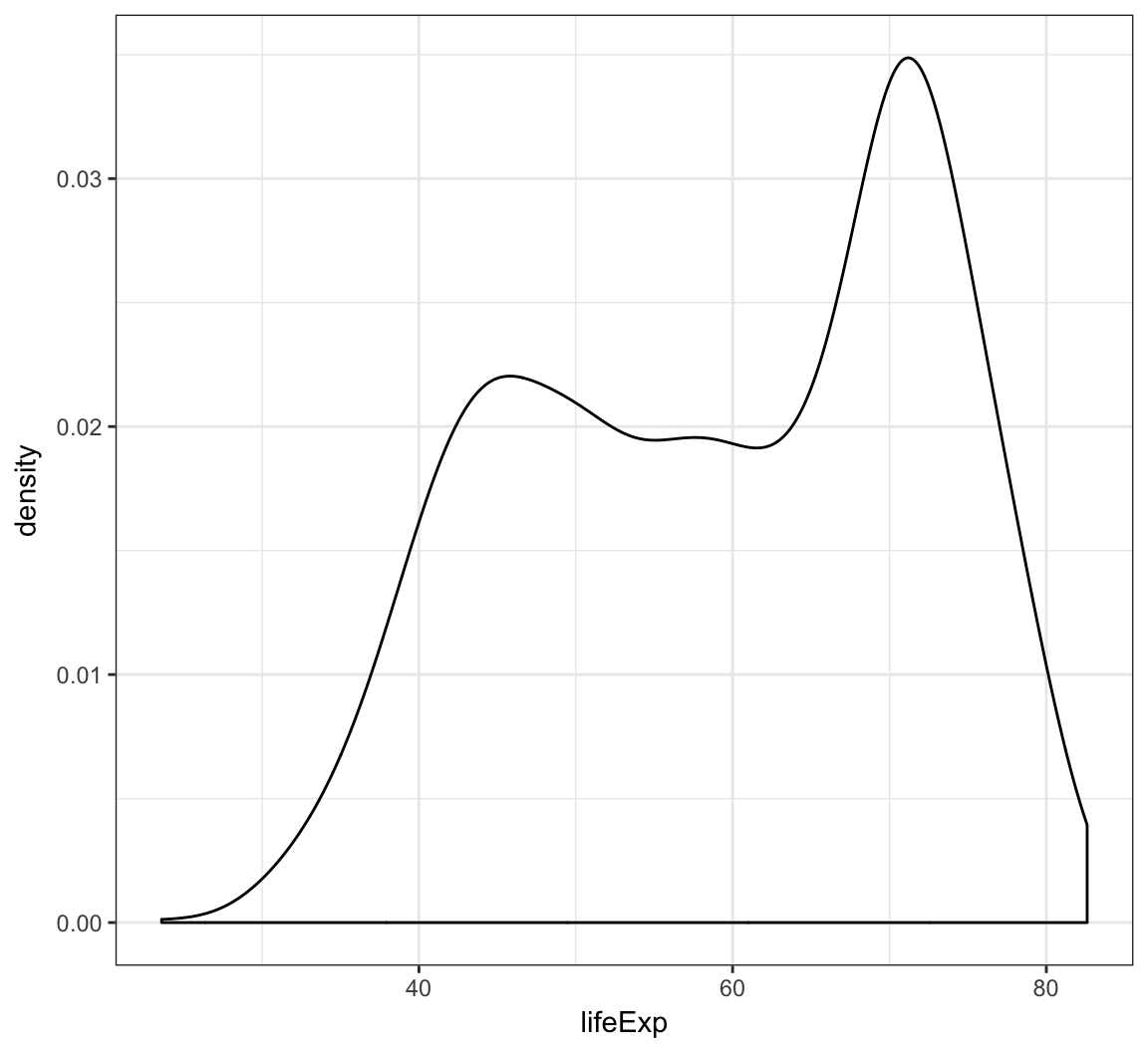
Employ the arguments color="blue" and fill="lightblue" outside of the aes() call to include some colors:
> ggplot(gapminder) +
+ geom_density(mapping = aes(x=lifeExp), color="blue",
+ fill="lightblue")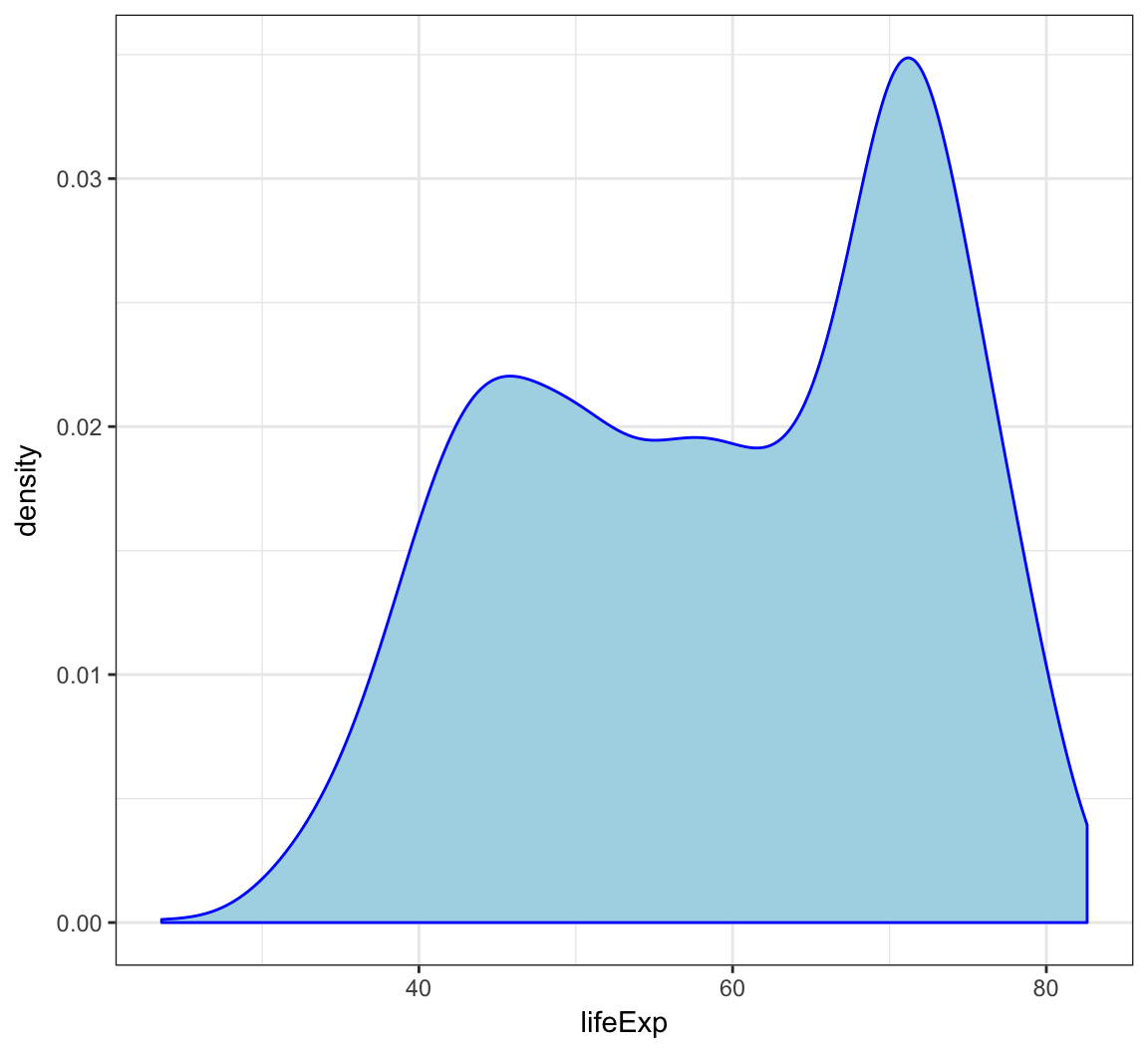
By utilizing color=as.factor(year) we plot a density of lifeExp stratified by each year value:
> ggplot(gapminder) +
+ geom_density(aes(x=lifeExp, color=as.factor(year)),
+ size=1.2)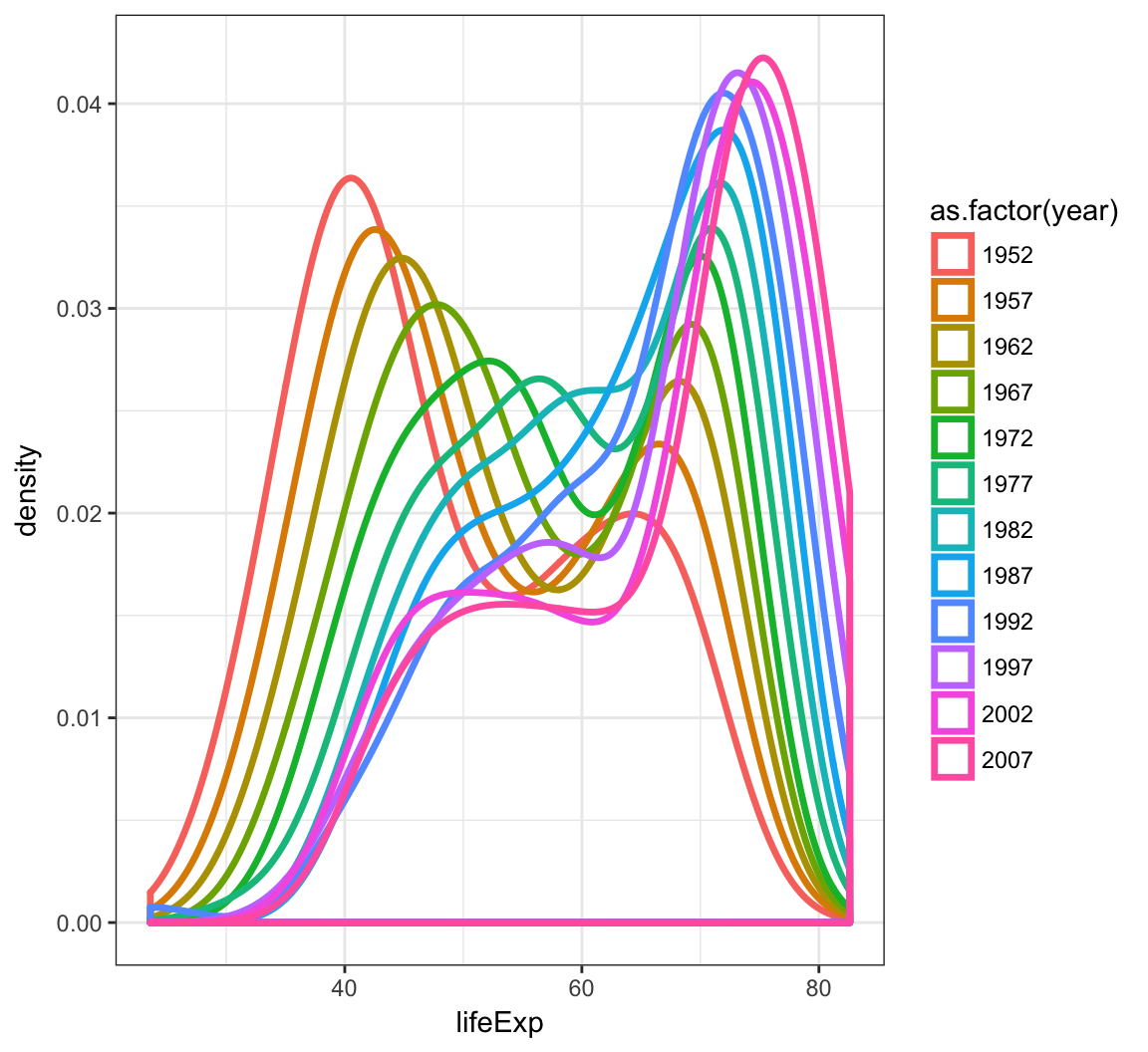
Overlay a density plot and a histogram together:
> ggplot(gapminder, mapping = aes(x=lifeExp)) +
+ geom_histogram(aes(y=..density..), color="black",
+ fill="white") +
+ geom_density(fill="lightblue", alpha=.5)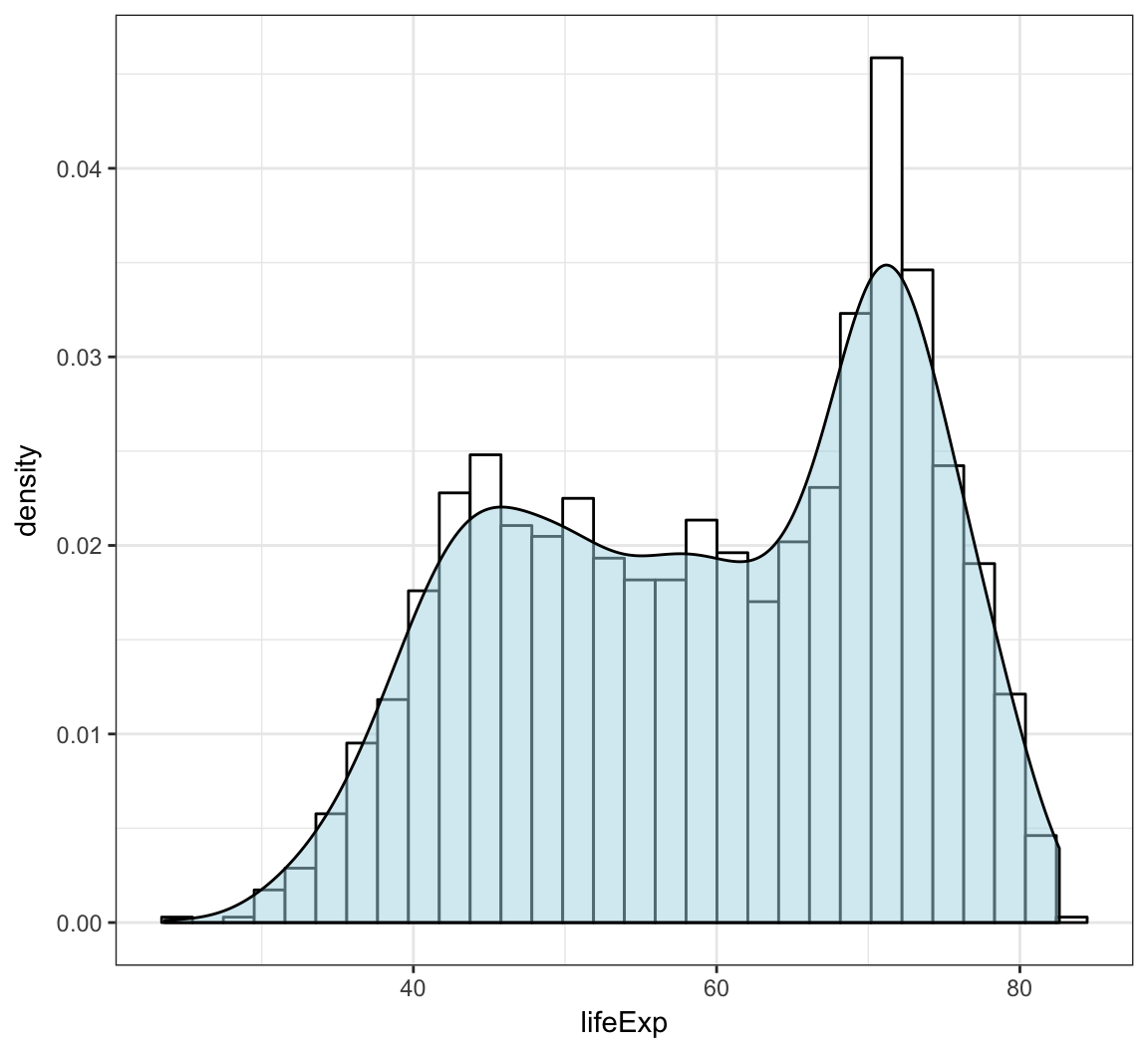
Line Plots
babynames Revisited
Let’s first create a data frame that captures the number of times “John” is registered in males per year:
> library("babynames")
> john <- babynames %>% filter(sex=="M", name=="John")
> head(john)
# A tibble: 6 × 5
year sex name n prop
<dbl> <chr> <chr> <int> <dbl>
1 1880 M John 9655 0.08154630
2 1881 M John 8769 0.08098299
3 1882 M John 9557 0.07831617
4 1883 M John 8894 0.07907324
5 1884 M John 9388 0.07648751
6 1885 M John 8756 0.07551791
We can geom_lines() to plot a line showing the popularity of “John” over time:
> ggplot(data = john) +
+ geom_line(mapping = aes(x=year, y=prop), size=1.5)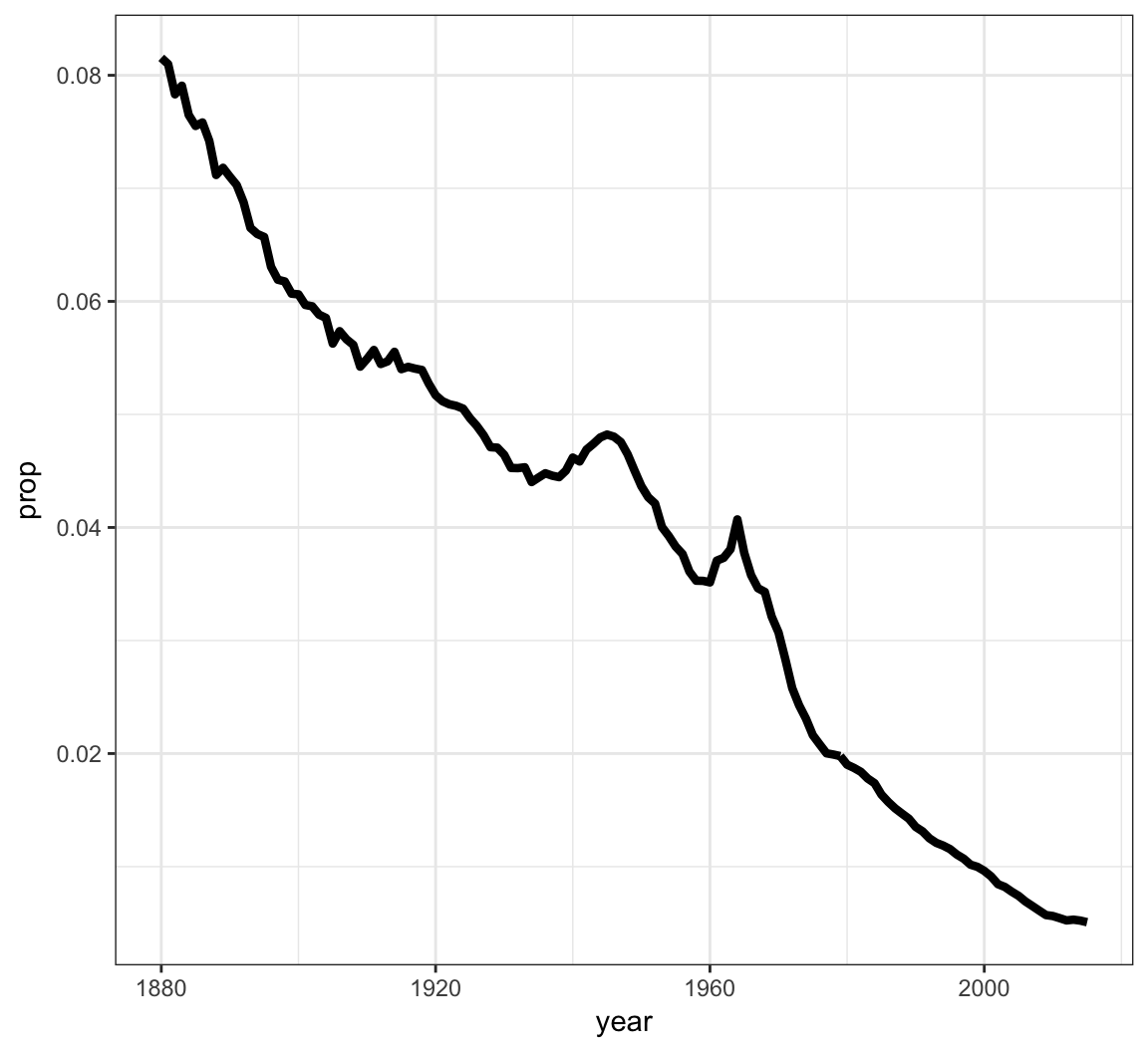
Now let’s look at a name that occurs nontrivially in males and females:
> kelly <- babynames %>% filter(name=="Kelly")
> ggplot(data = kelly) +
+ geom_line(mapping = aes(x=year, y=prop, color=sex),
+ size=1.5)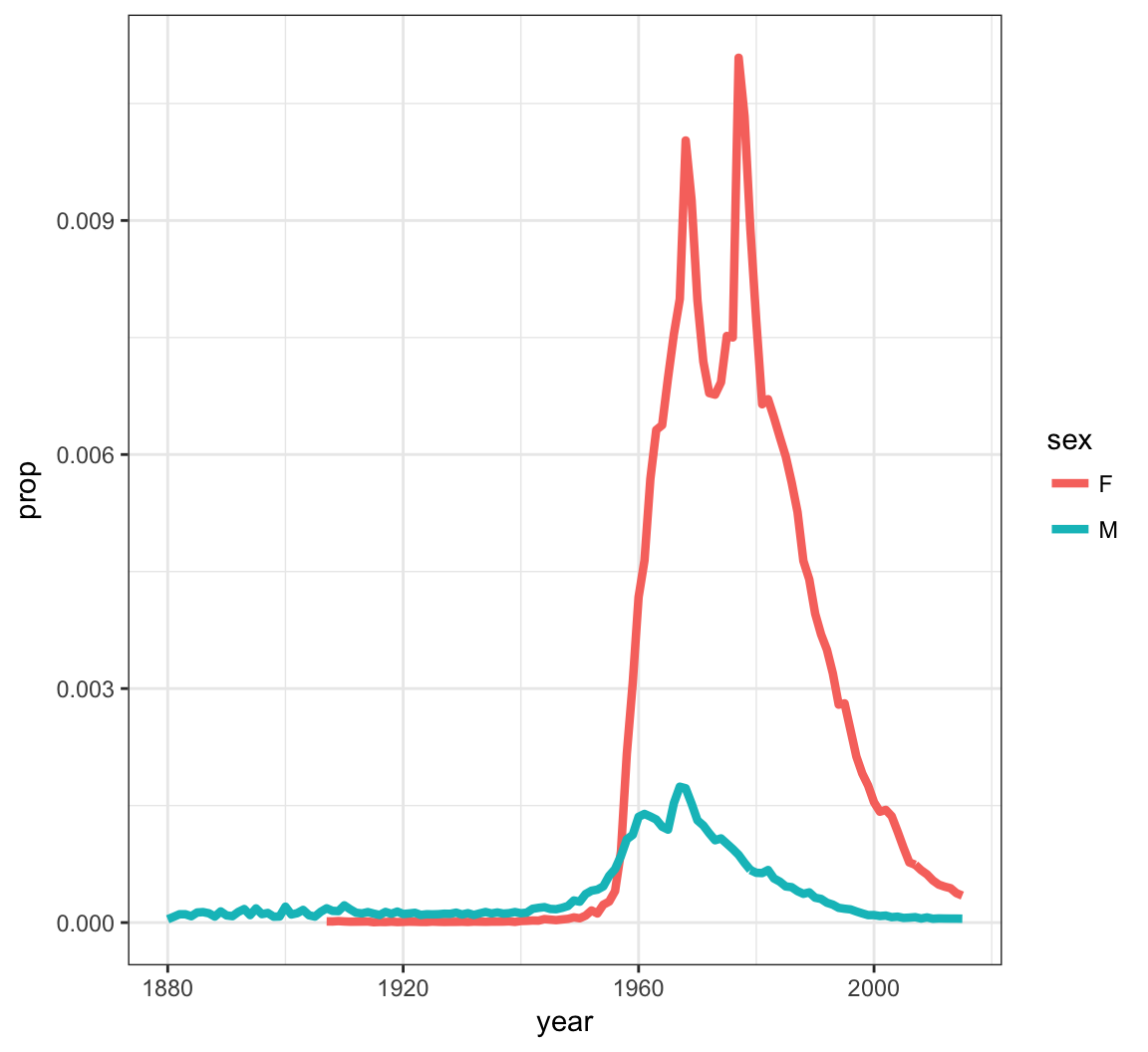
Scatterplots
The layer geom_point() produces a scatterplot, and the aes() call requires x and y assignment:
> ggplot(data = mpg) +
+ geom_point(mapping = aes(x = displ, y = hwy))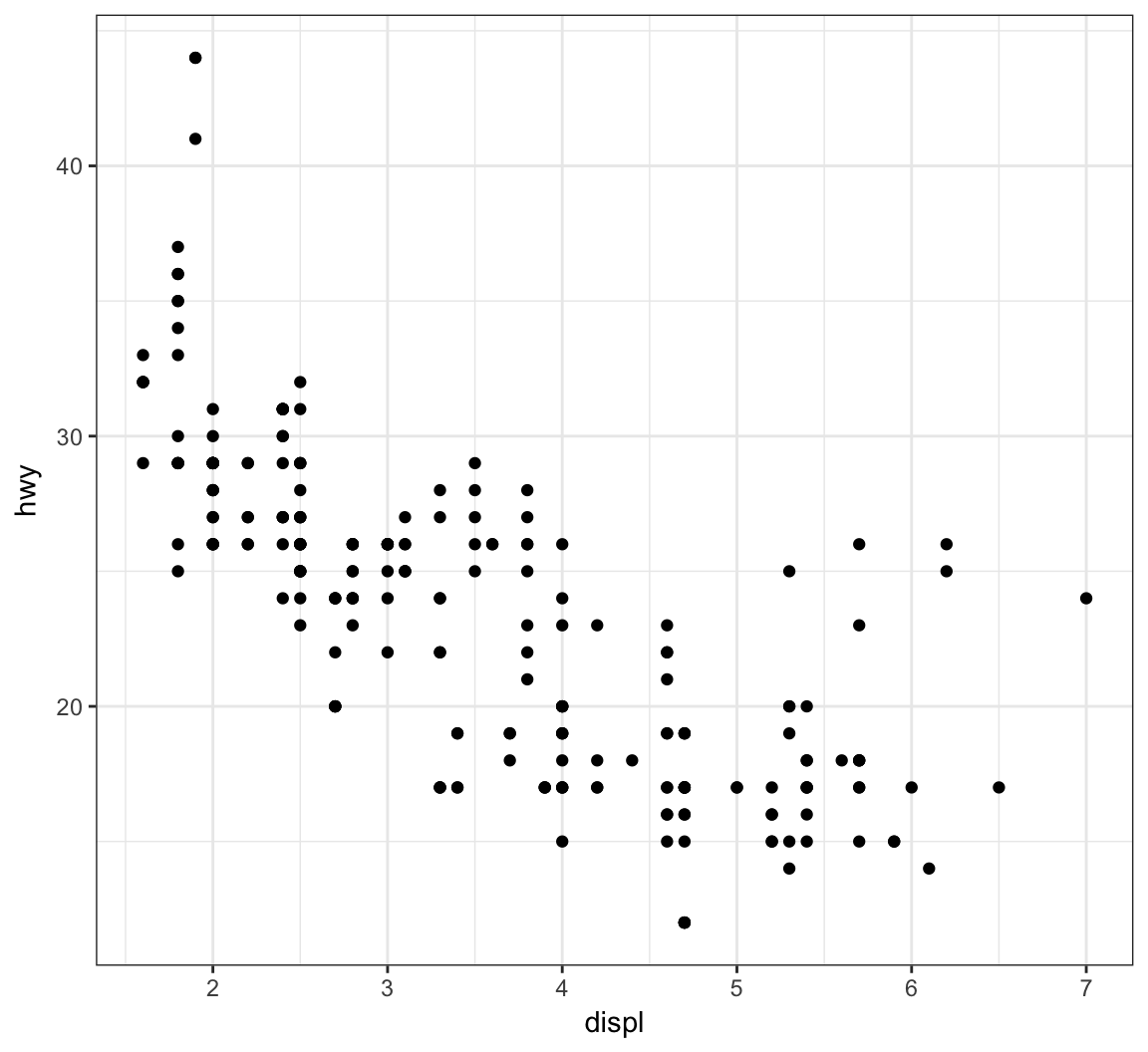
Give the points a color:
> ggplot(data = mpg) +
+ geom_point(mapping = aes(x = displ, y = hwy),
+ color = "blue")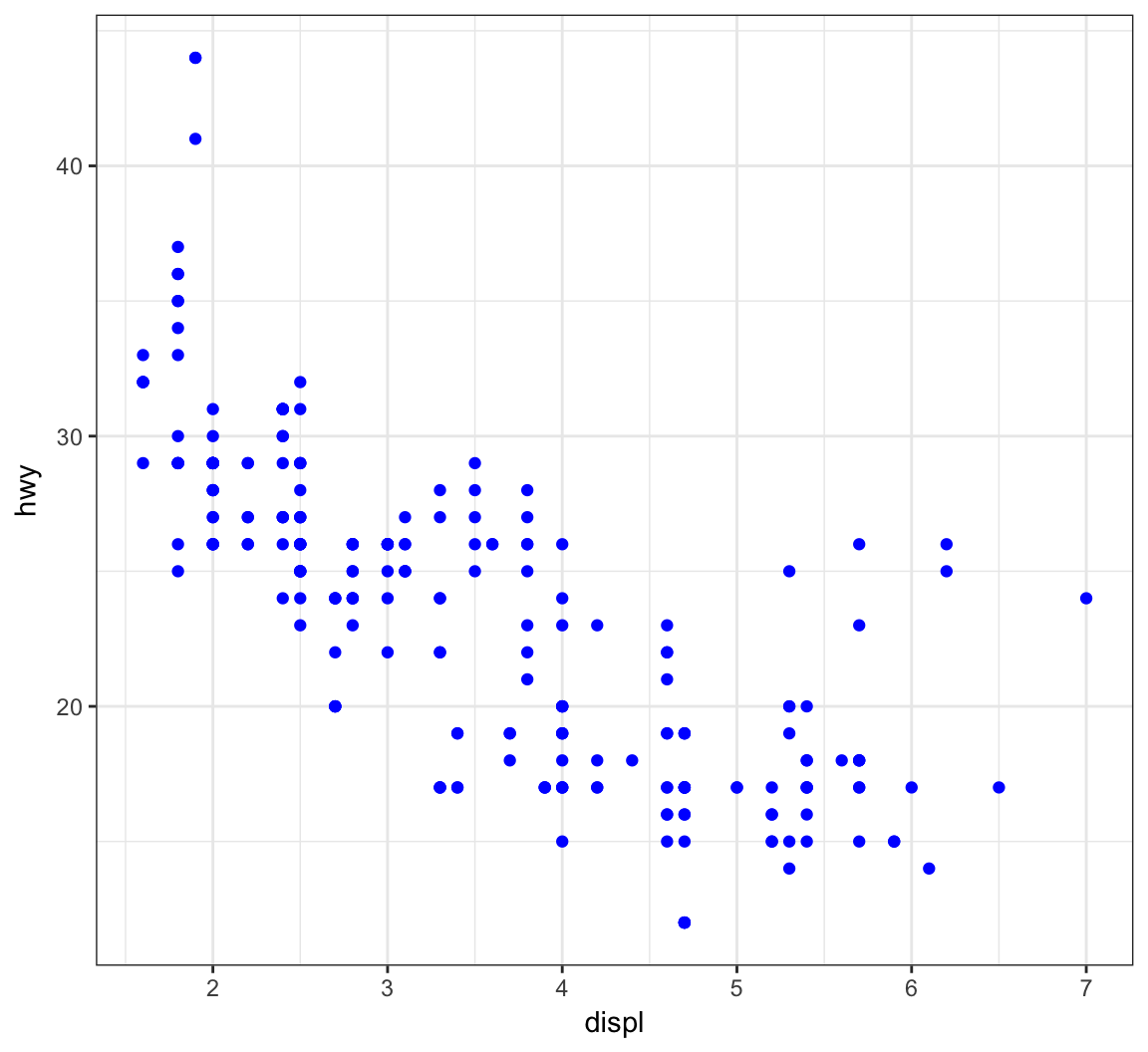
Color the points according to a factor variable by including color = class within the aes() call:
> ggplot(data = mpg) +
+ geom_point(mapping = aes(x = displ, y = hwy,
+ color = class))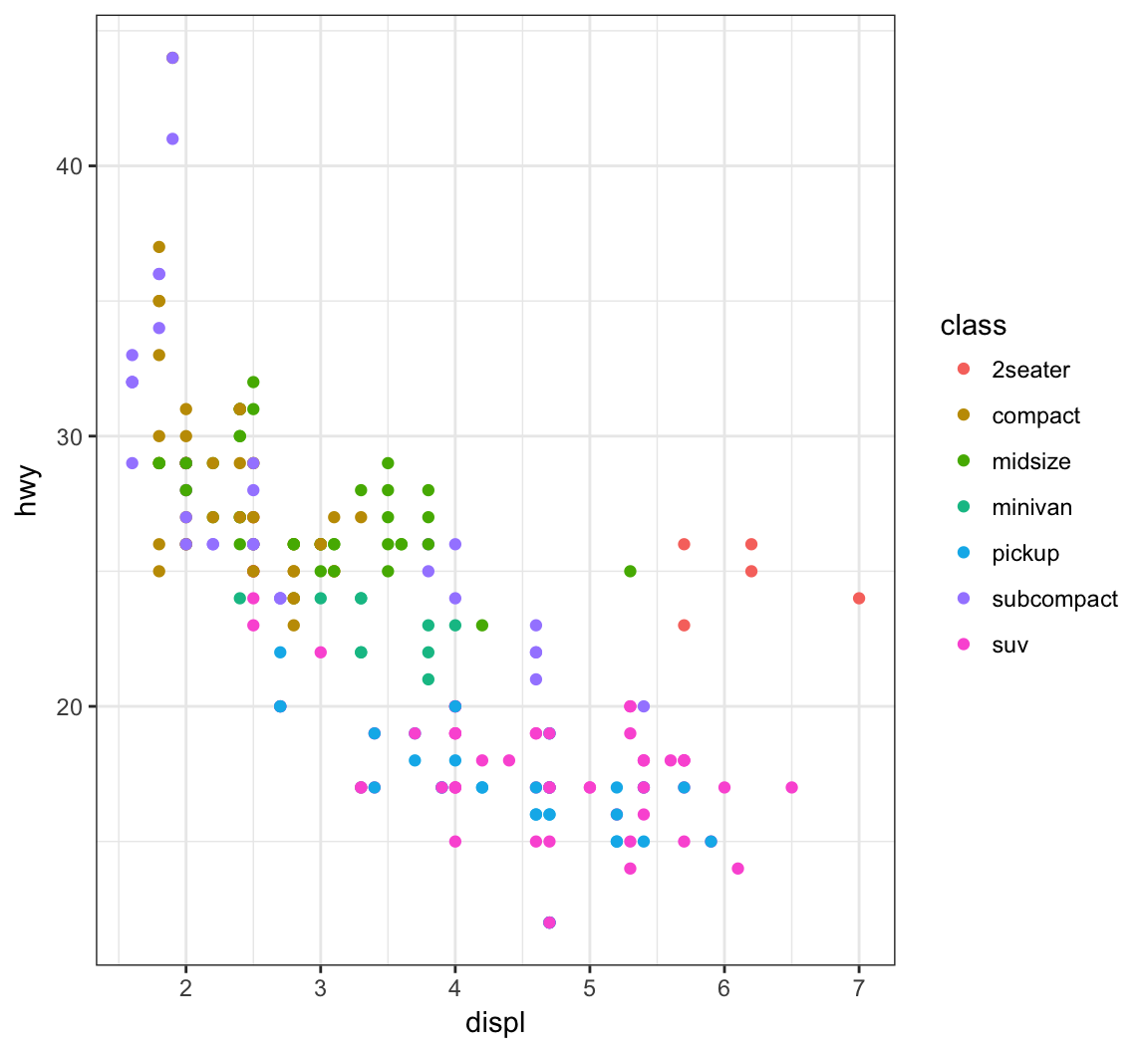
Increase the size of points with size=2 outside of the aes() call:
> ggplot(data = mpg) +
+ geom_point(mapping = aes(x = displ, y = hwy,
+ color = class), size=2)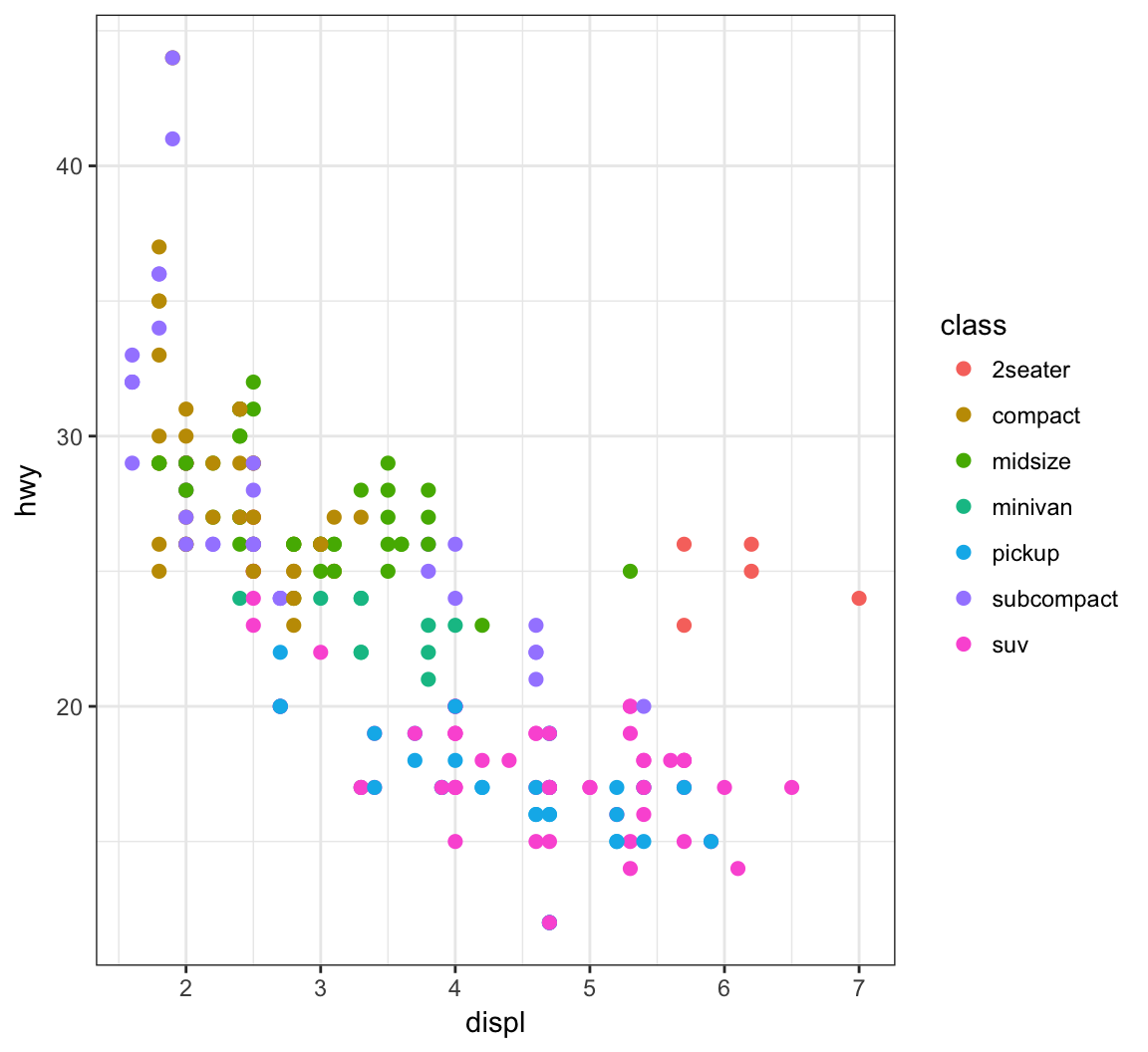
Vary the size of the points according to the pop variable:
> gapminder %>% filter(year==2007) %>% ggplot() +
+ geom_point(aes(x = log(gdpPercap), y = lifeExp,
+ size = pop))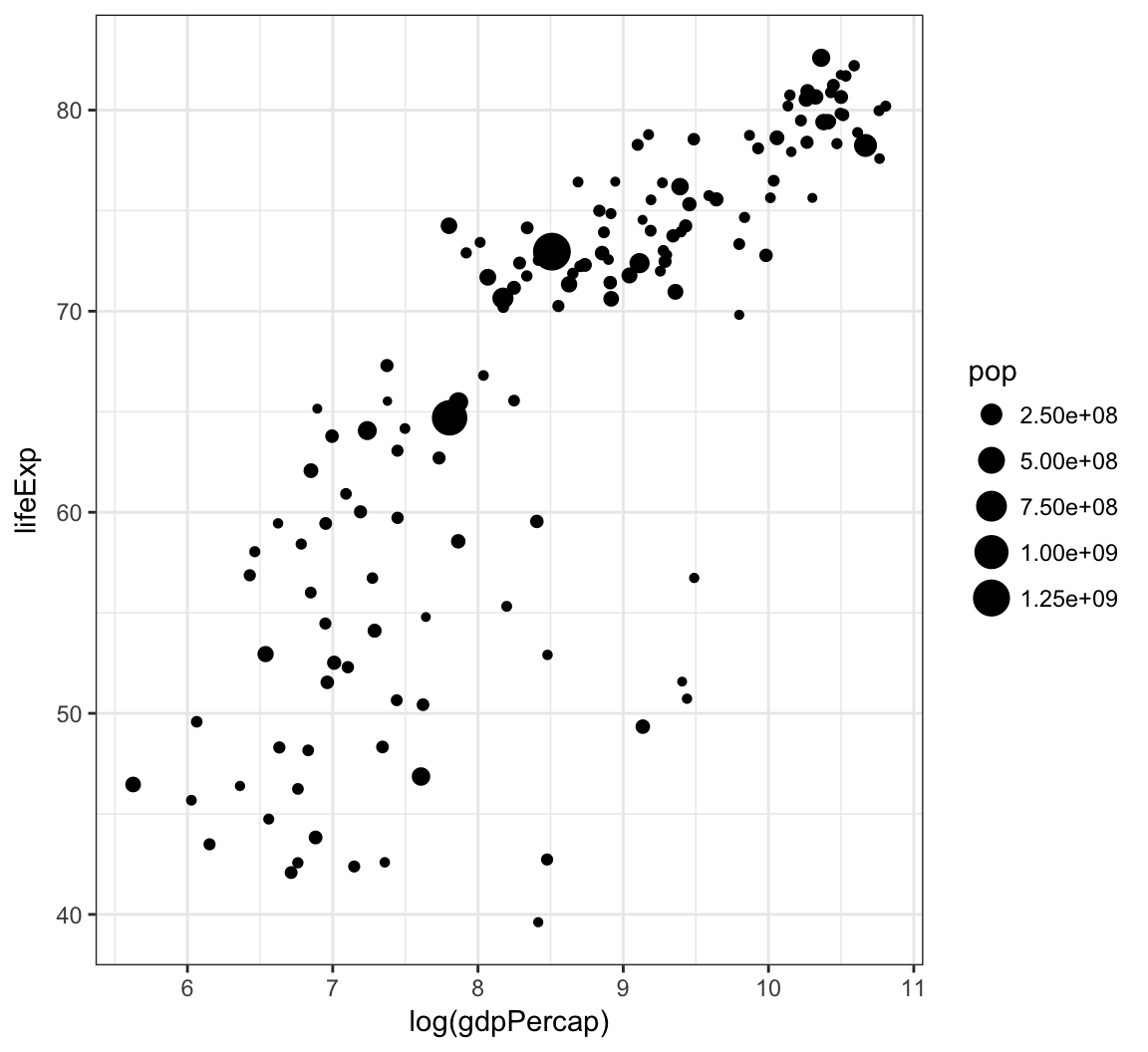
Vary the transparency of the points according to the class factor variable by setting alpha=class within the aes() call:
> ggplot(data = mpg) +
+ geom_point(mapping = aes(x = displ, y = hwy,
+ alpha = class))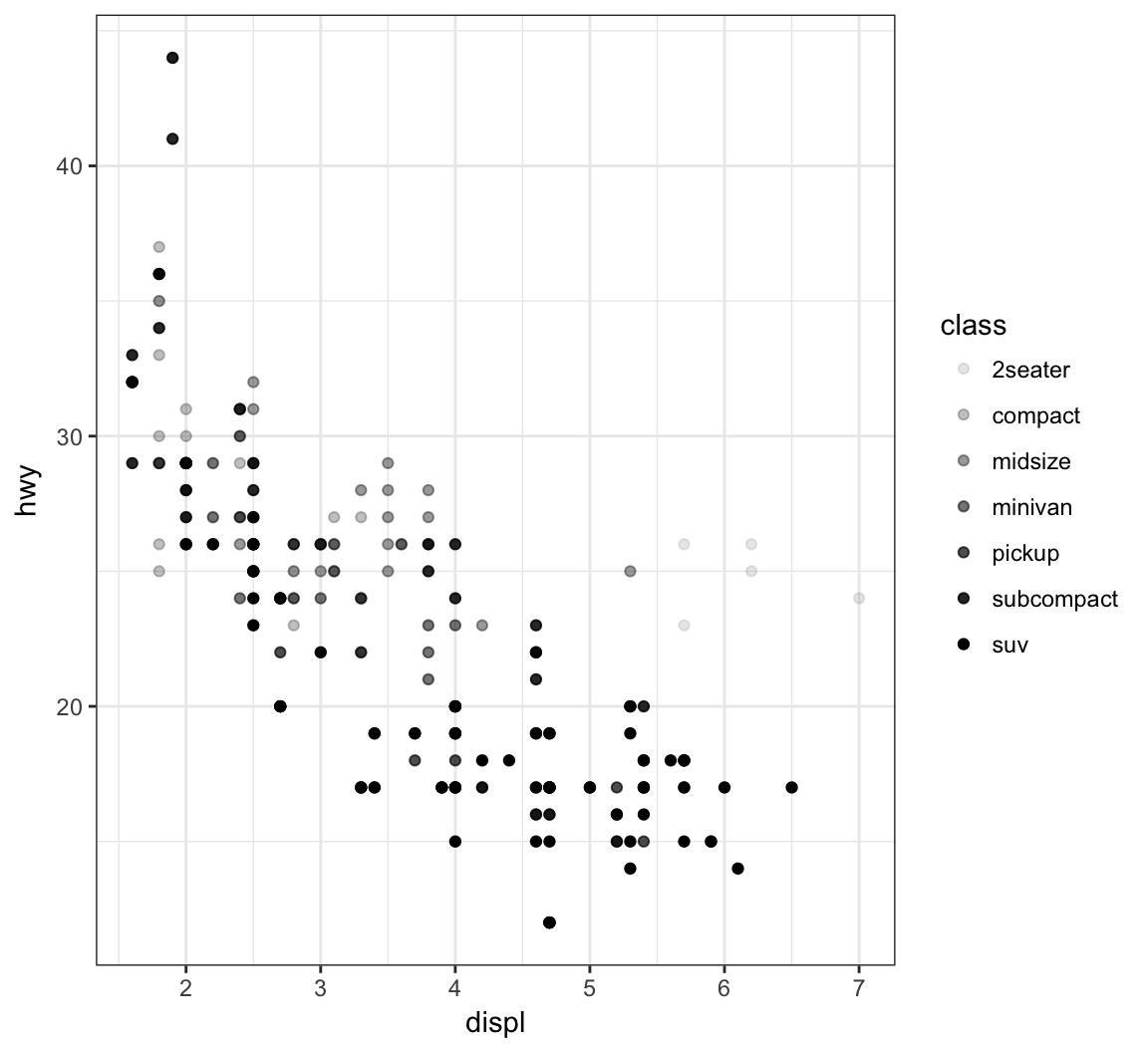
Vary the shape of the points according to the class factor variable by setting alpha=class within the aes() call (maximum 6 possible shapes – oops!):
> ggplot(data = mpg) +
+ geom_point(mapping = aes(x = displ, y = hwy,
+ shape = class))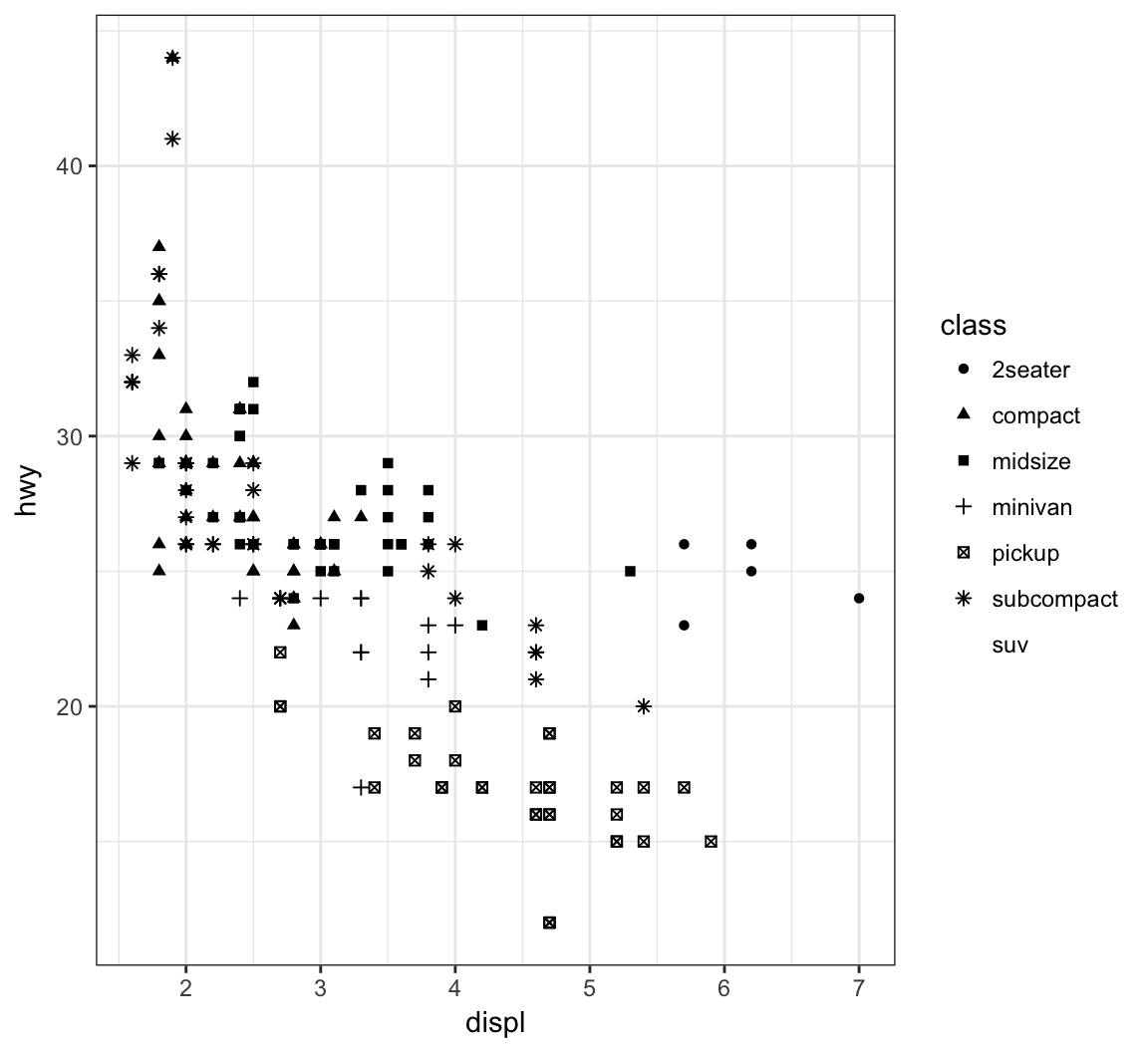
Color the points according to the cut variable by setting color=cut within the aes() call:
> ggplot(data = diamonds) +
+ geom_point(mapping = aes(x=carat, y=price, color=cut),
+ alpha=0.7)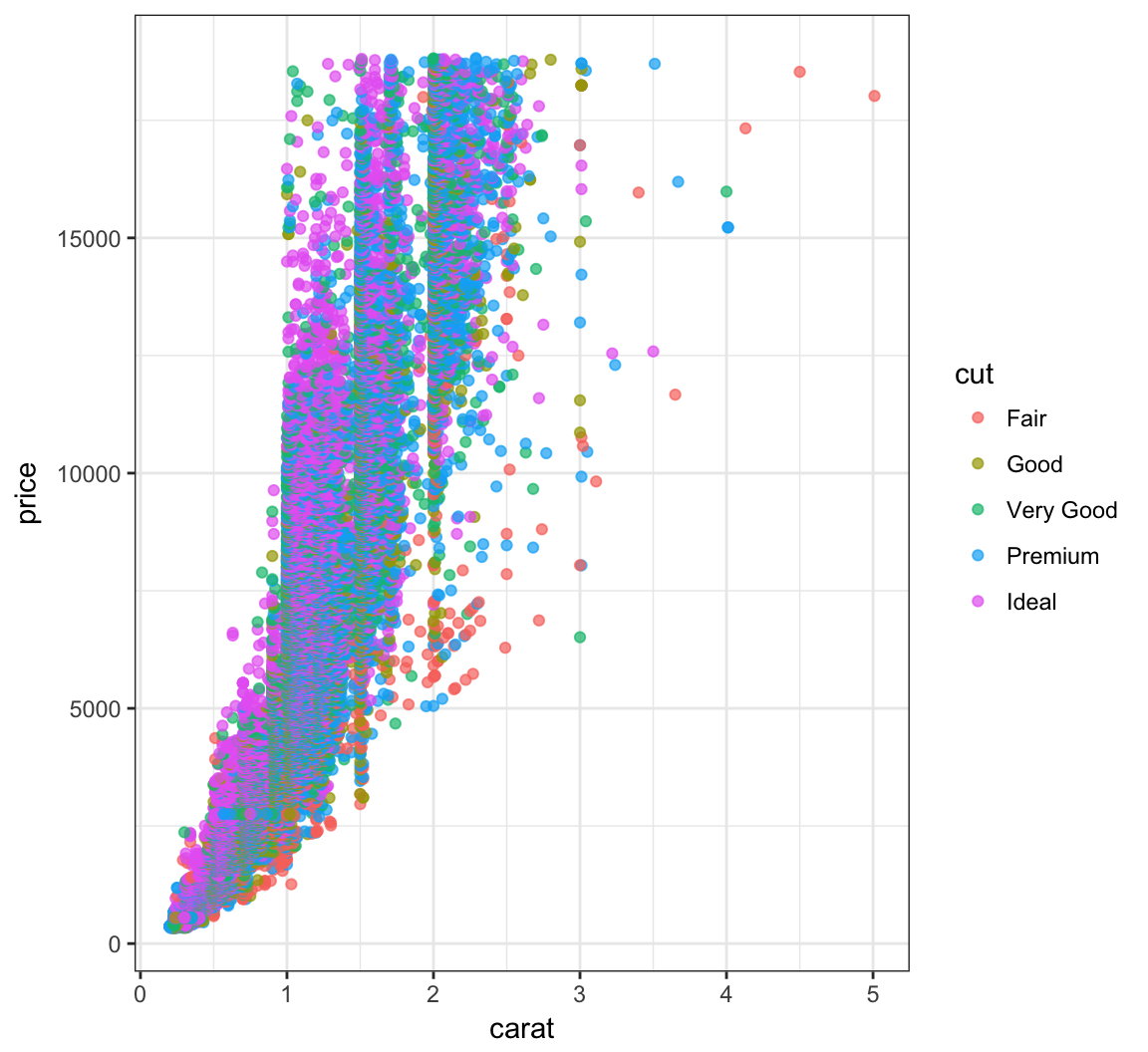
Color the points according to the clarity variable by setting color=clarity within the aes() call:
> ggplot(data = diamonds) +
+ geom_point(mapping=aes(x=carat, y=price, color=clarity),
+ alpha=0.3)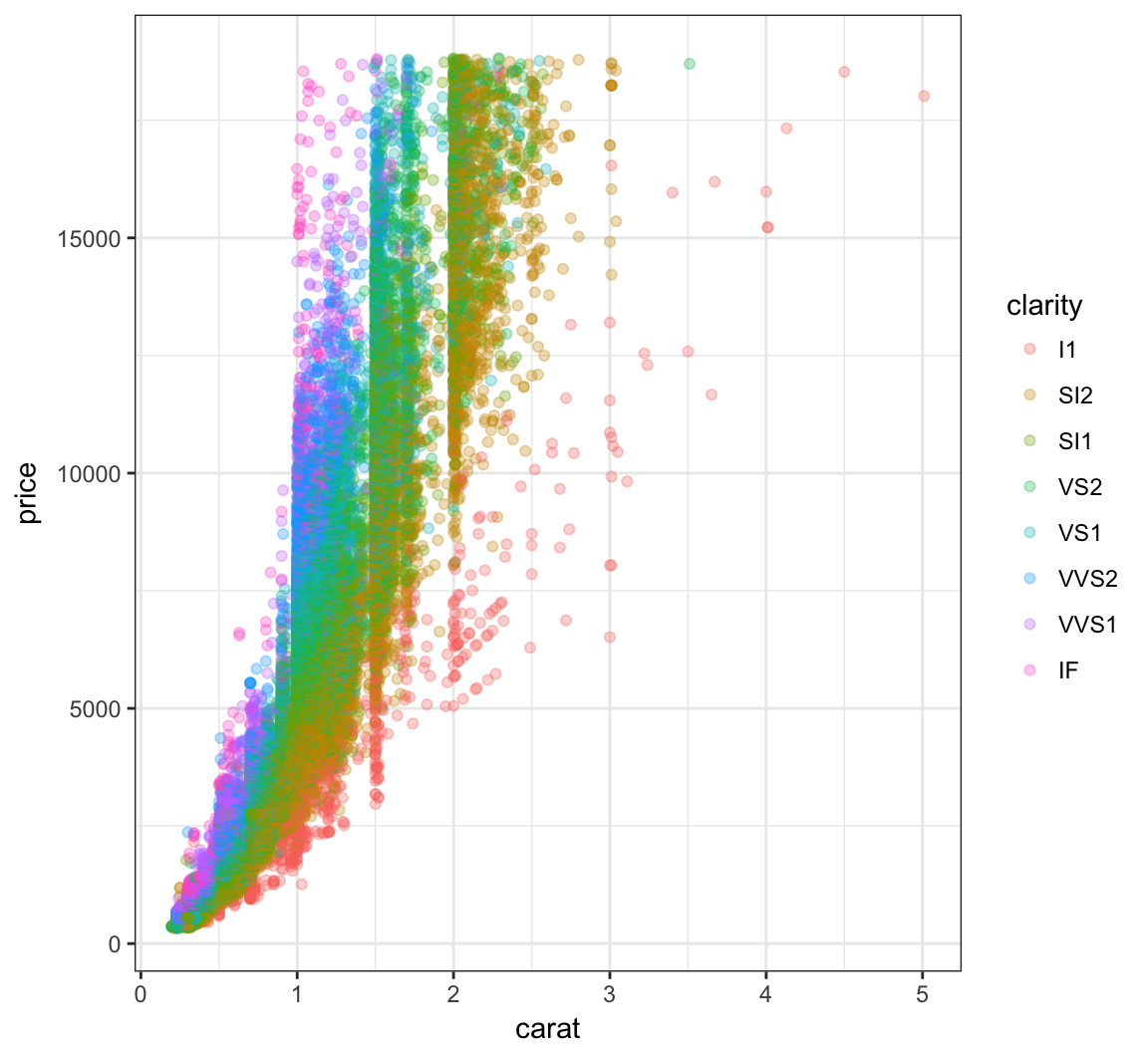
Override the alpha=0.3 in the legend:
> ggplot(data=diamonds) +
+ geom_point(mapping=aes(x=carat, y=price, color=clarity),
+ alpha=0.3) +
+ guides(color=guide_legend(override.aes = list(alpha = 1)))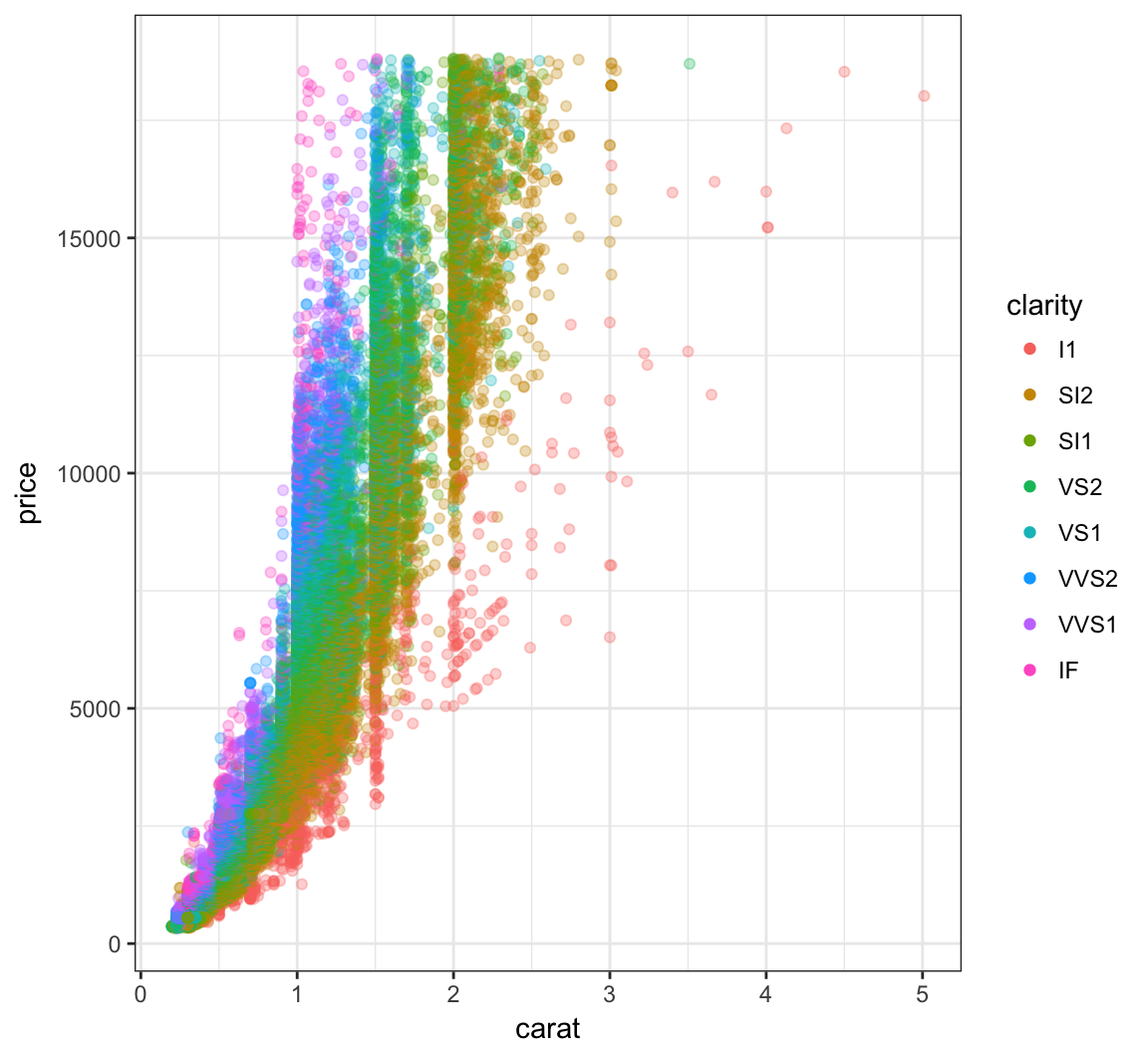
Axis Scales
A different way to take the log of gdpPercap:
> gapminder %>% filter(year==2007) %>% ggplot() +
+ geom_point(aes(x = gdpPercap, y = lifeExp,
+ size = pop)) +
+ scale_x_log10()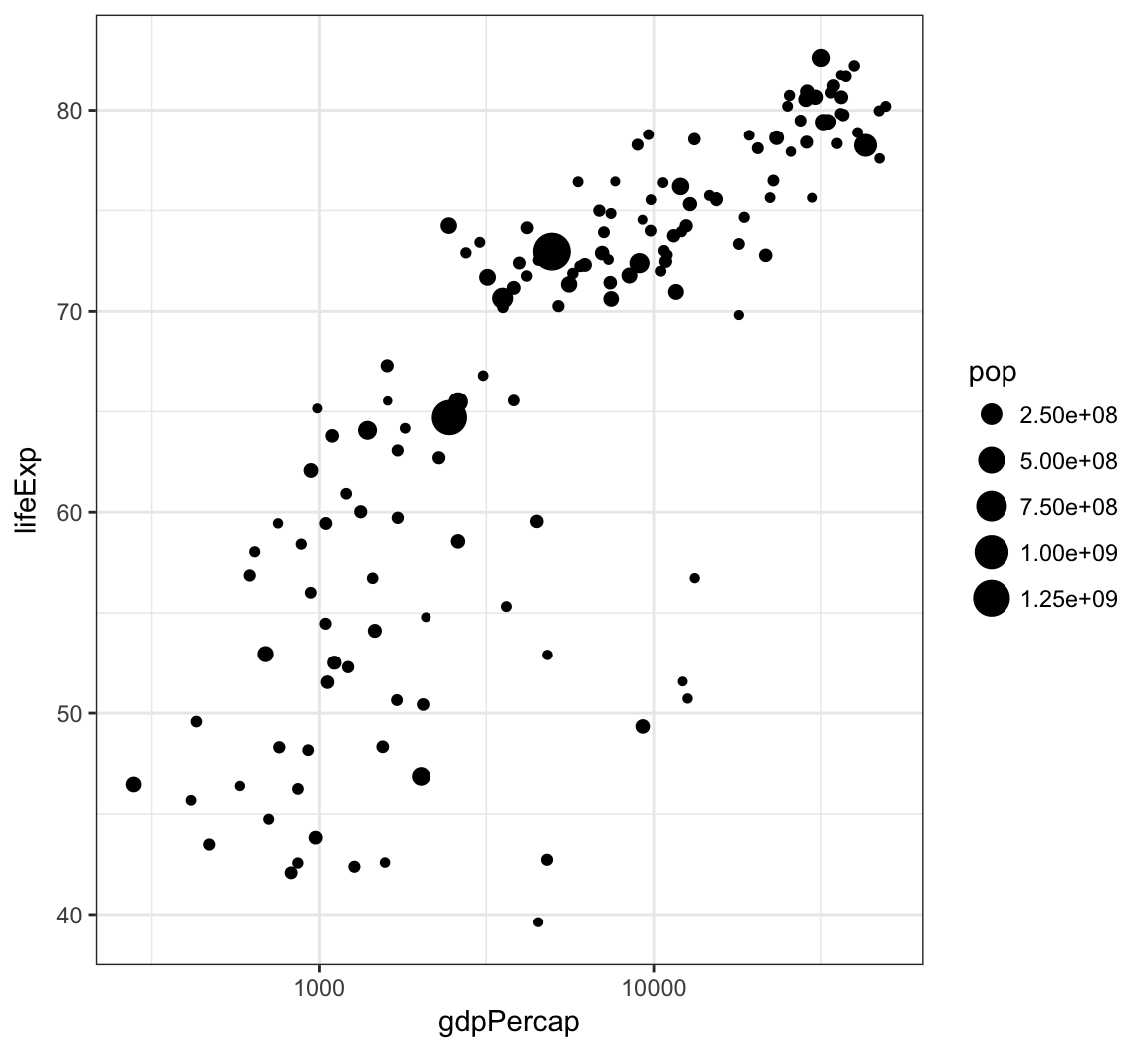
The price variable seems to be significantly right-skewed:
> ggplot(diamonds) +
+ geom_boxplot(aes(x=color, y=price)) 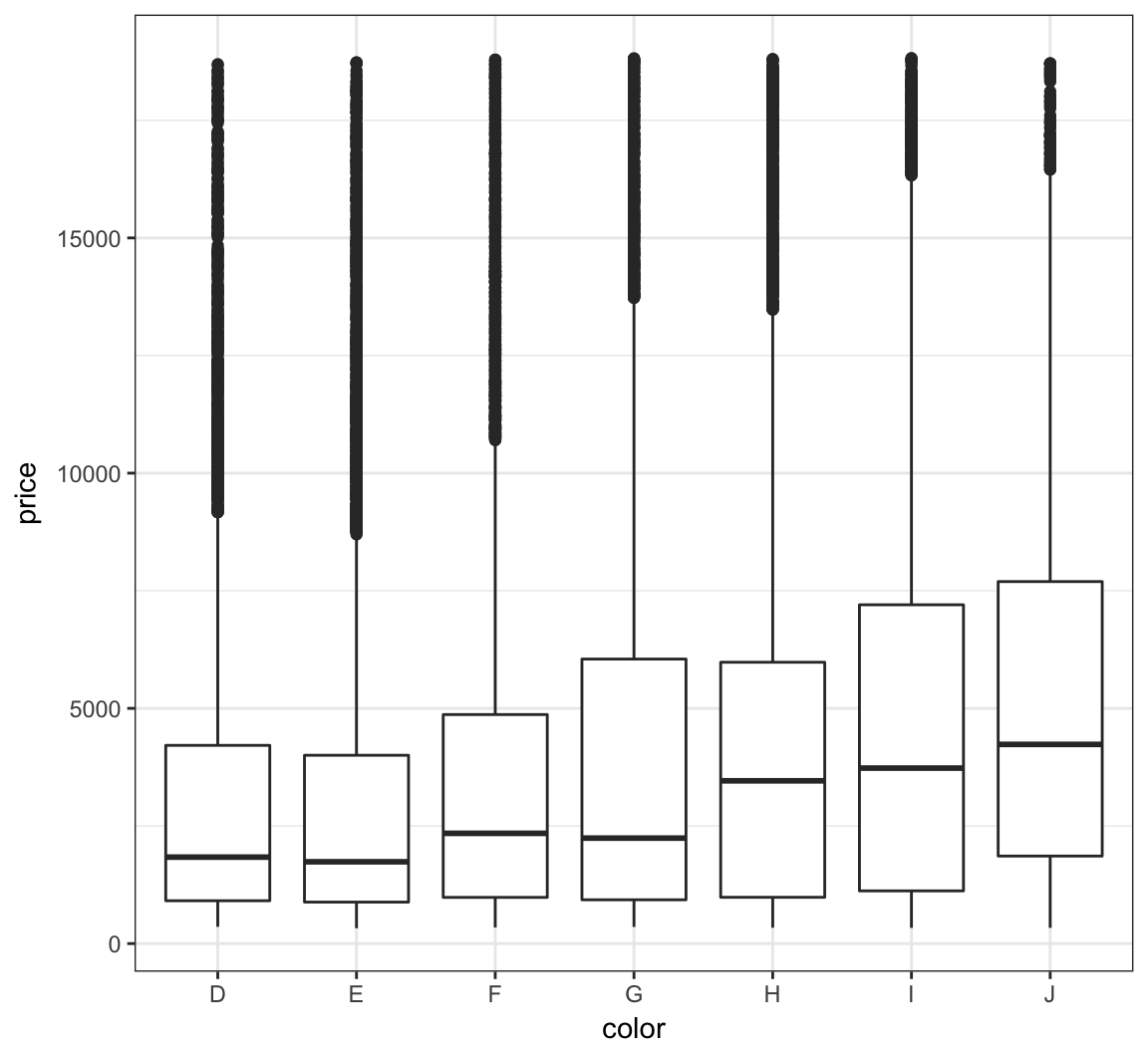
We can try to reduce this skewness by rescaling the variables. We first try to take the log(base=10) of the price variable via scale_y_log10():
> ggplot(diamonds) +
+ geom_boxplot(aes(x=color, y=price)) +
+ scale_y_log10()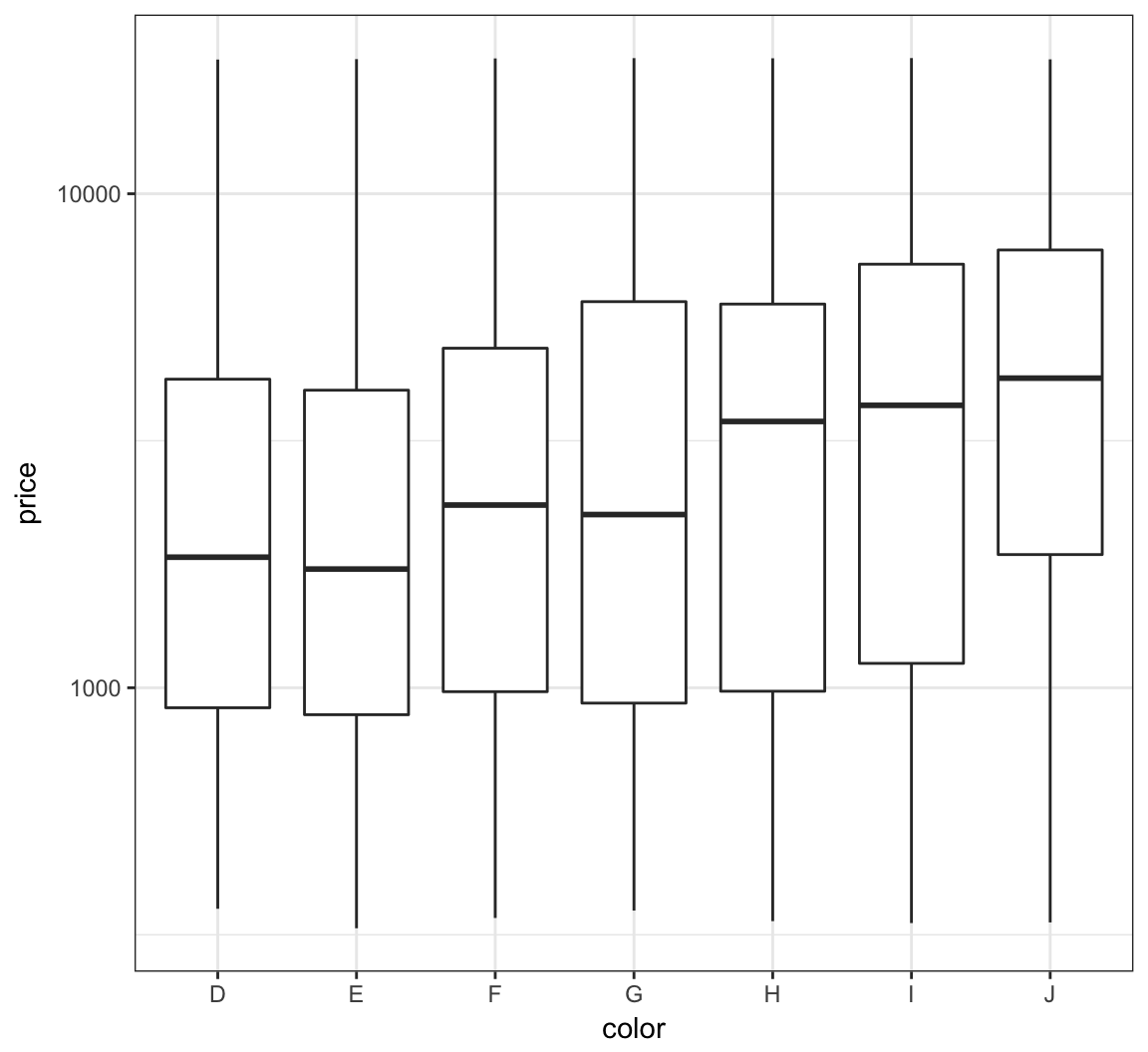
Let’s repeat this on the analogous violing plots:
> ggplot(diamonds) +
+ geom_violin(aes(x=color, y=price)) +
+ scale_y_log10()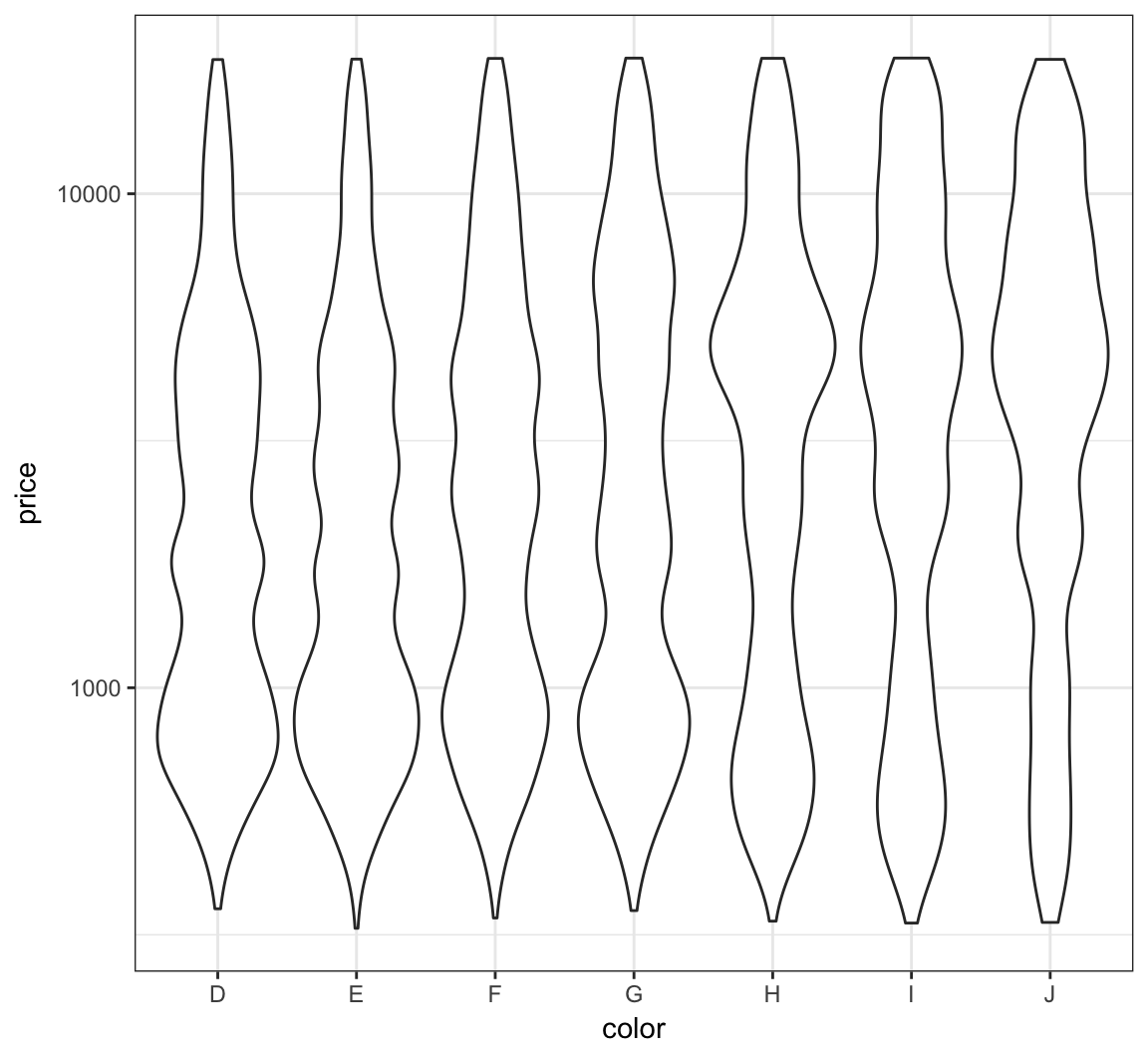
The relationship between carat and price is nonlinear. Let’s explore different transformations to find an approximately linear relationship.
> ggplot(data = diamonds) +
+ geom_point(mapping=aes(x=carat, y=price, color=clarity),
+ alpha=0.3)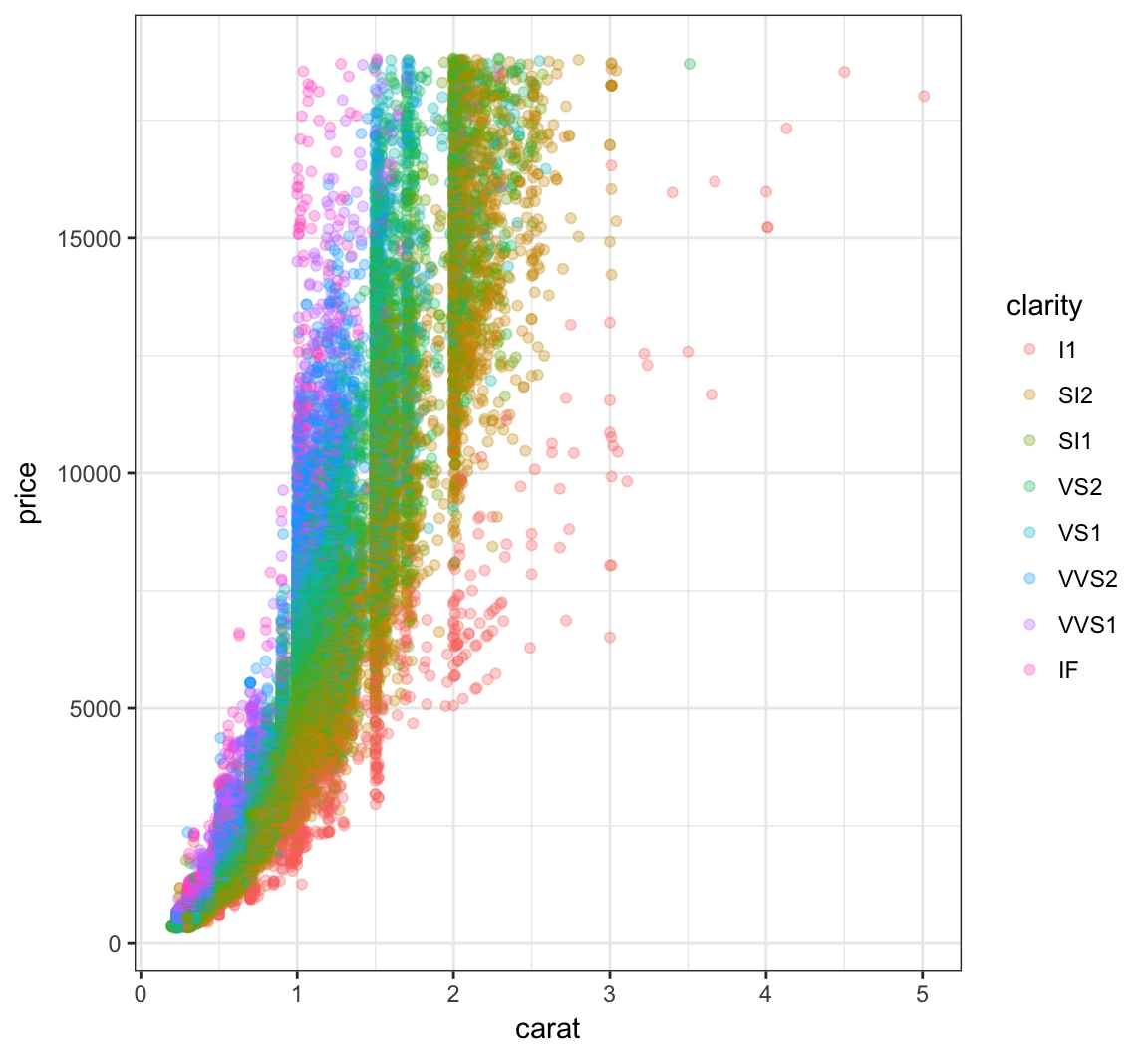
First try to take the squareroot of the the price variable:
> ggplot(data = diamonds) +
+ geom_point(aes(x=carat, y=price, color=clarity),
+ alpha=0.3) +
+ scale_y_sqrt()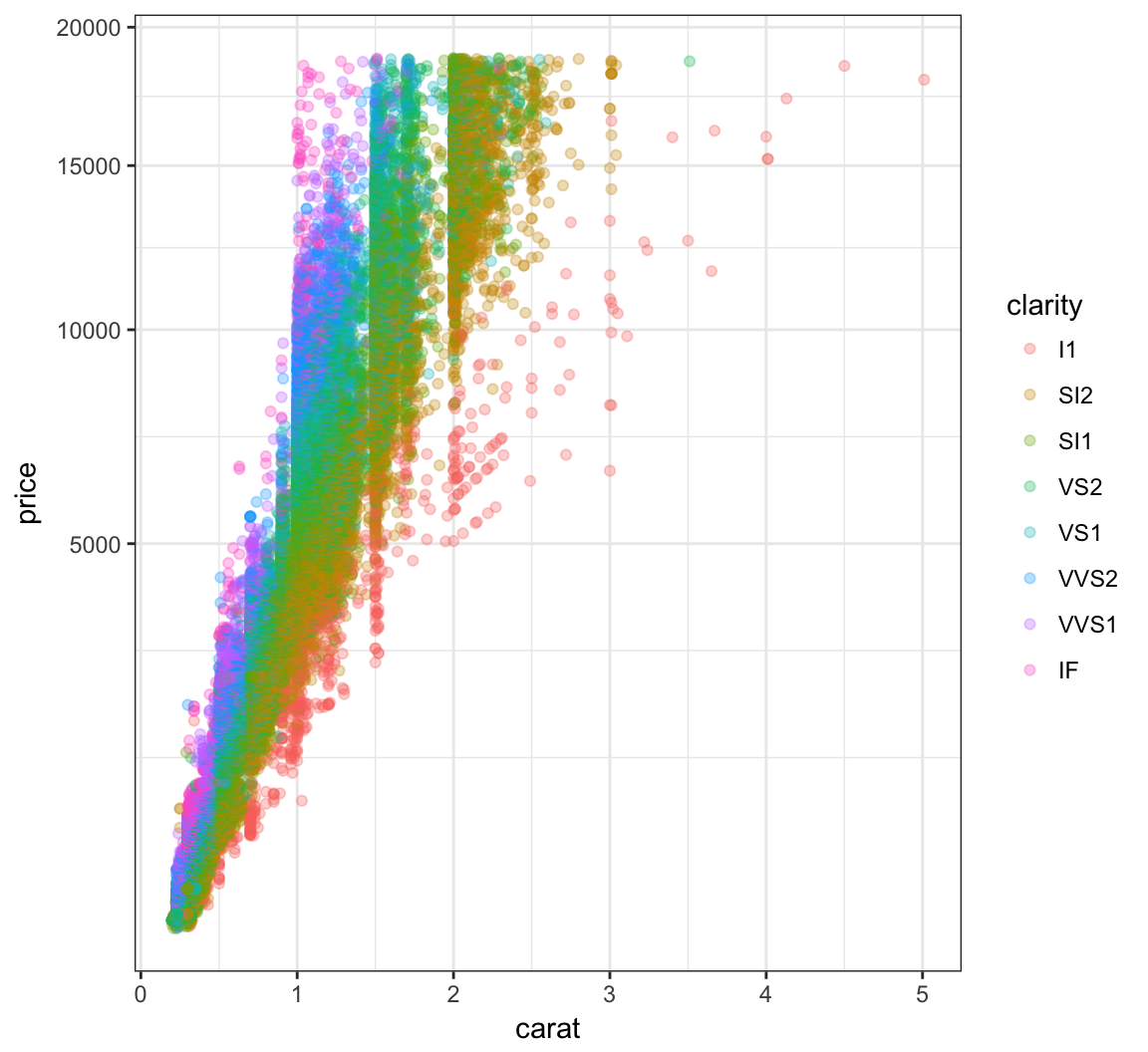
Now let’s try to take log(base=10) on both the carat and price variables:
> ggplot(data = diamonds) +
+ geom_point(aes(x=carat, y=price, color=clarity), alpha=0.3) +
+ scale_y_log10(breaks=c(1000,5000,10000)) +
+ scale_x_log10(breaks=1:5)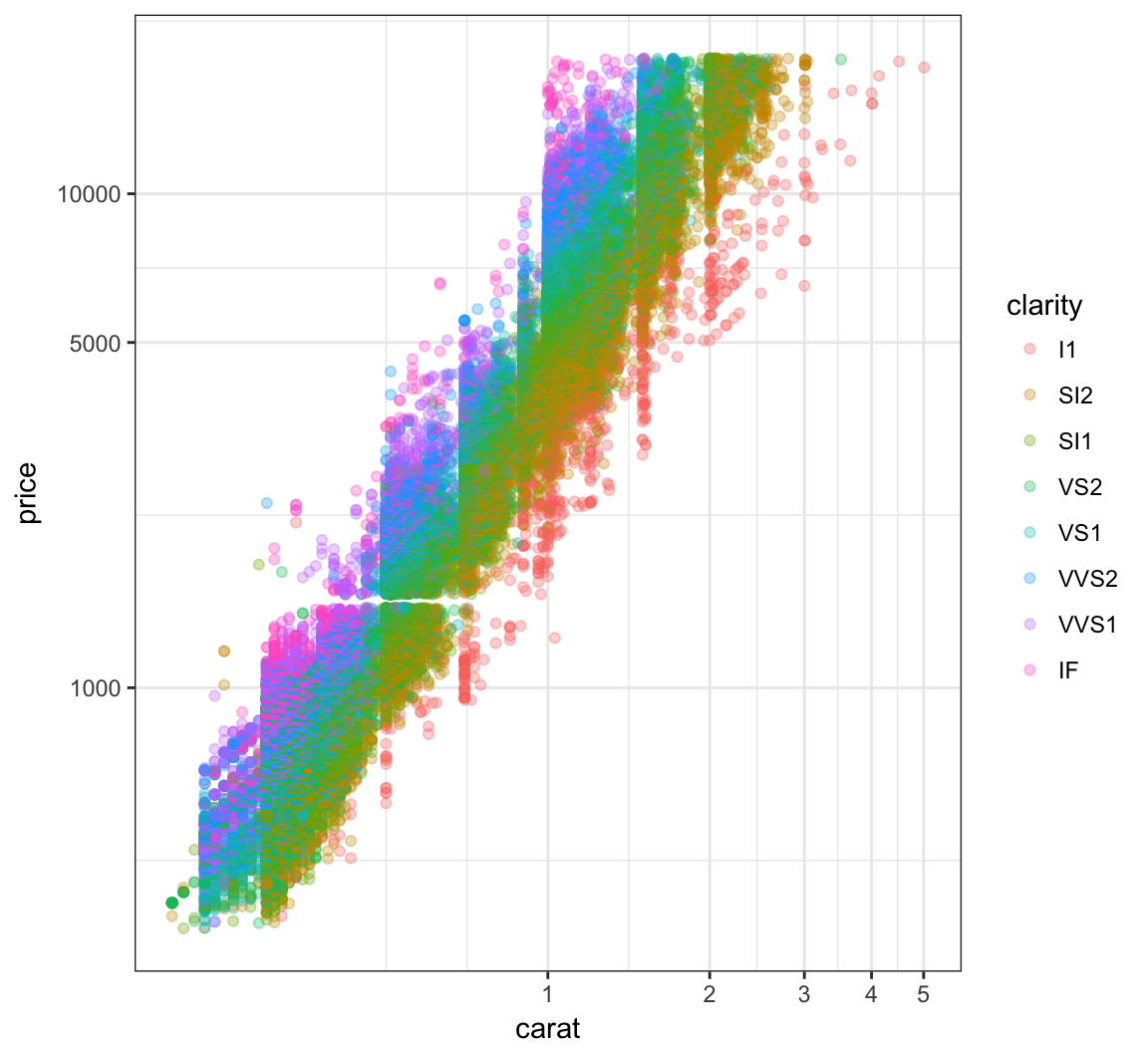
Forming a violin plot of price stratified by clarity and transforming the price variable yields an interesting relationship in this data set:
> ggplot(diamonds) +
+ geom_violin(aes(x=clarity, y=price, fill=clarity),
+ adjust=1.5) +
+ scale_y_log10()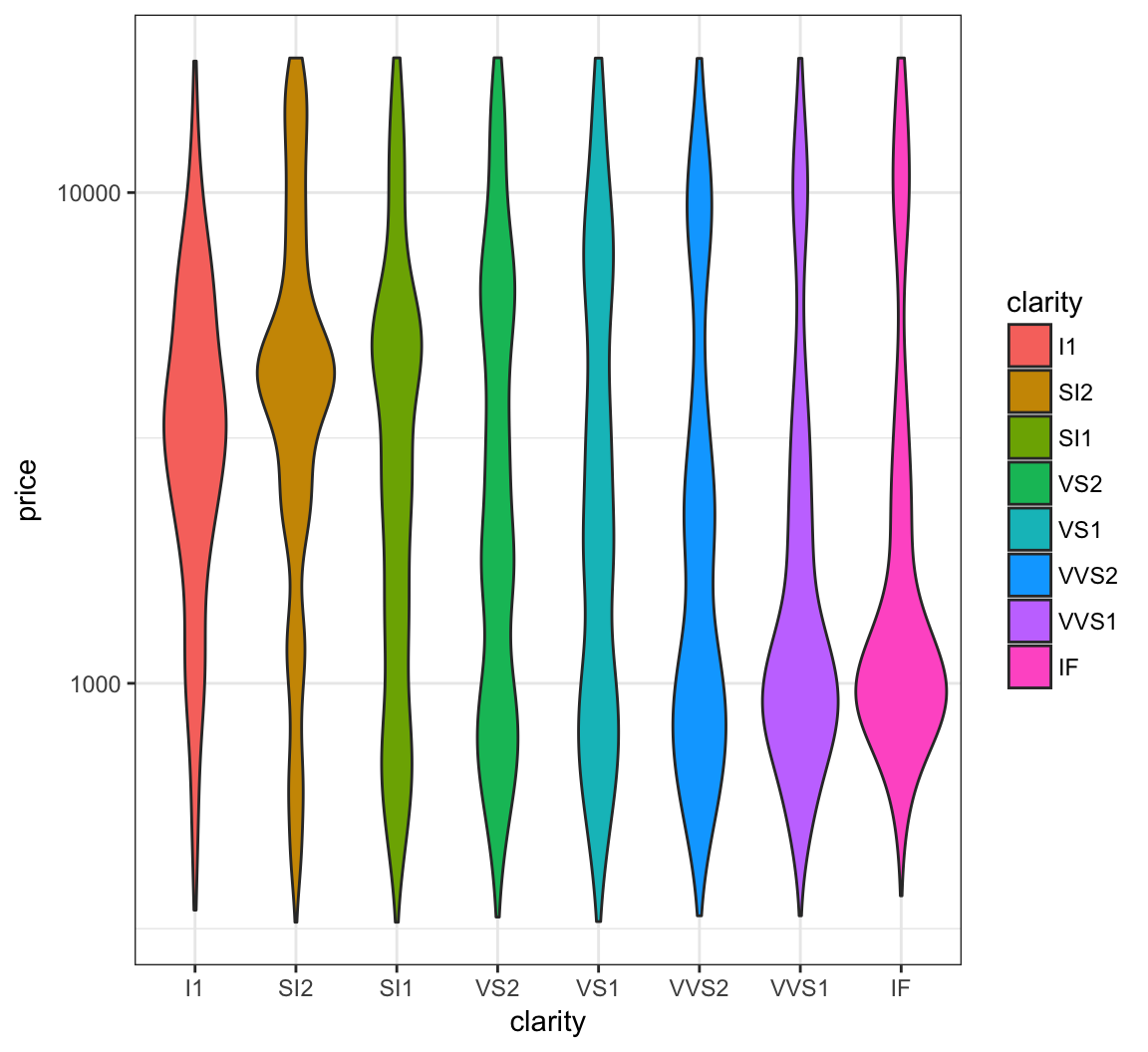
Scatterplot Smoothers
Fitting “Smoothers” and Other Models to Scatterplots
- Later this semester, we will spend several weeks learning how to explain or predict an outcome variable in terms of predictor variables
- We will briefly show here how to plot some simple model fits to scatterplots
- You may want to return to these slides later in the semester once we cover modeling in more detail
Recall the scatterplot showing the relationship between highway mpg and displacement. How can we plot a smoothed relationship between these two variables?
> ggplot(data = mpg) +
+ geom_point(mapping = aes(x = displ, y = hwy))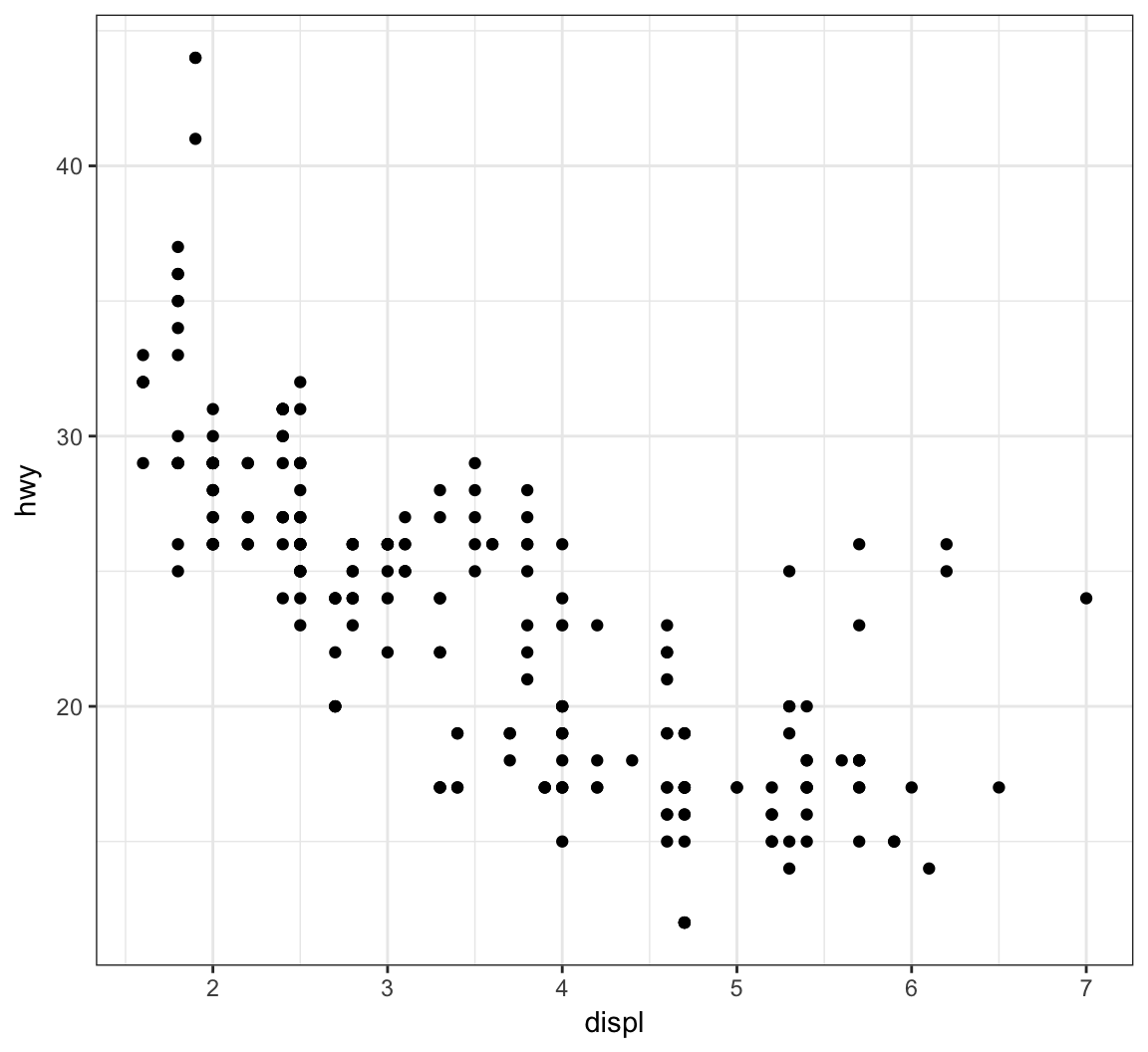
Plot a smoother with geom_smooth() using the default settings (other than removing the error bands):
> ggplot(data = mpg, mapping = aes(x = displ, y = hwy)) +
+ geom_point() +
+ geom_smooth(se=FALSE)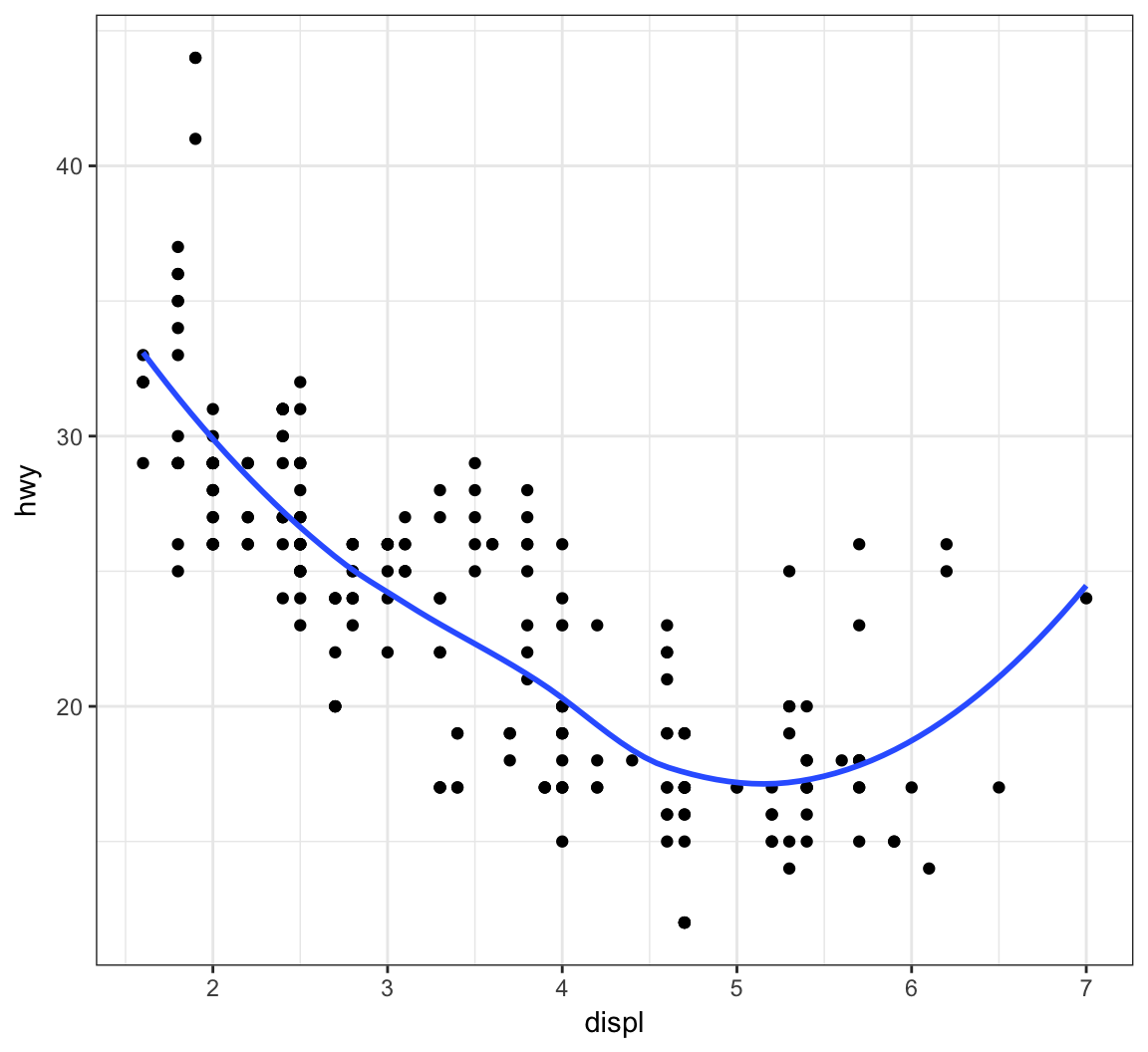
The default smoother here is a “loess” smoother. Let’s compare that to the least squares regresson line:
> ggplot(data = mpg, mapping = aes(x = displ, y = hwy)) +
+ geom_point() +
+ geom_smooth(aes(colour = "loess"), method = "loess", se = FALSE) +
+ geom_smooth(aes(colour = "lm"), method = "lm", se = FALSE)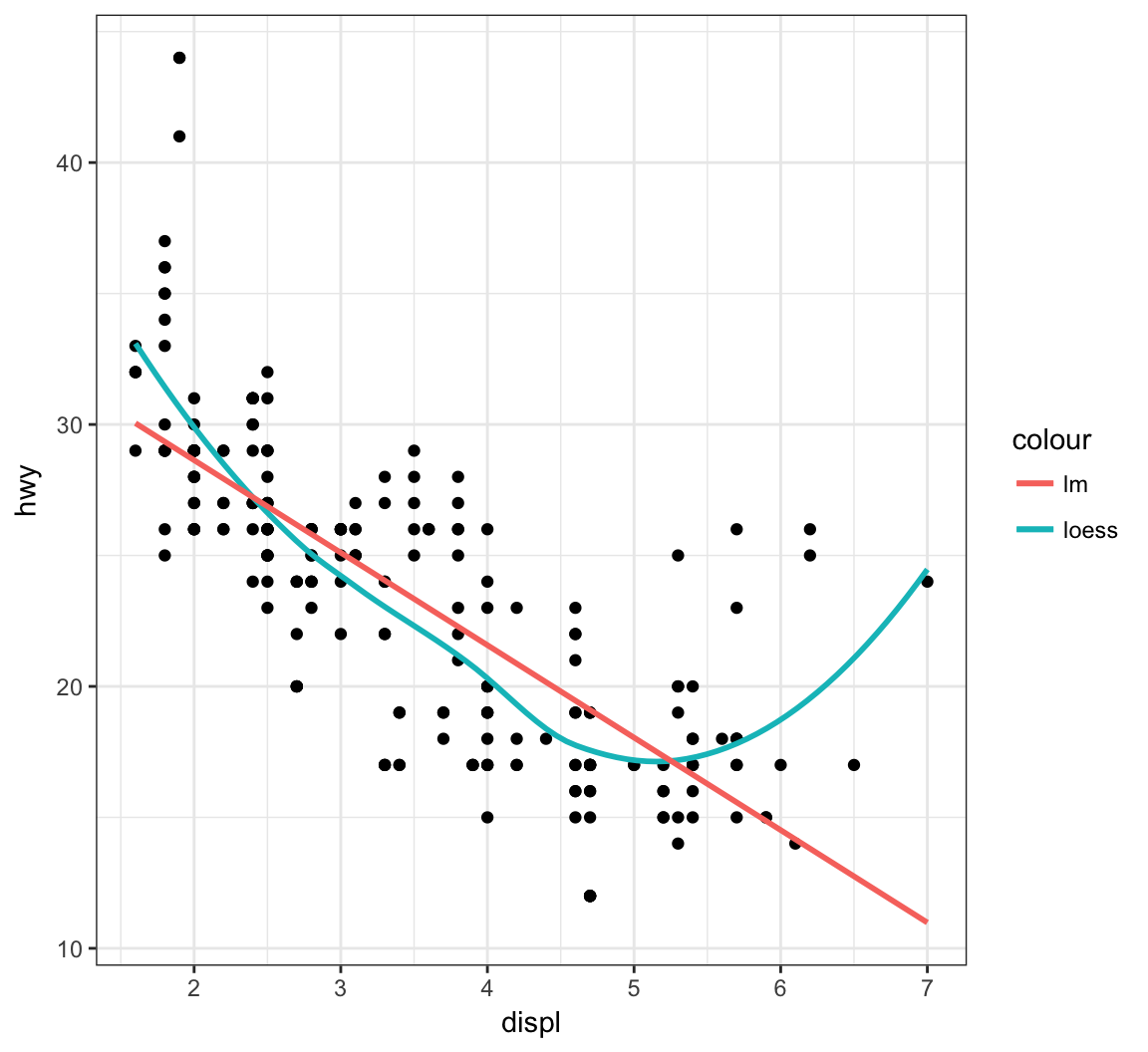
Now let’s plot a smoother to the points stratified by the drv variable:
> ggplot(data=mpg, mapping = aes(x = displ, y = hwy,
+ linetype = drv)) +
+ geom_point() +
+ geom_smooth(se=FALSE)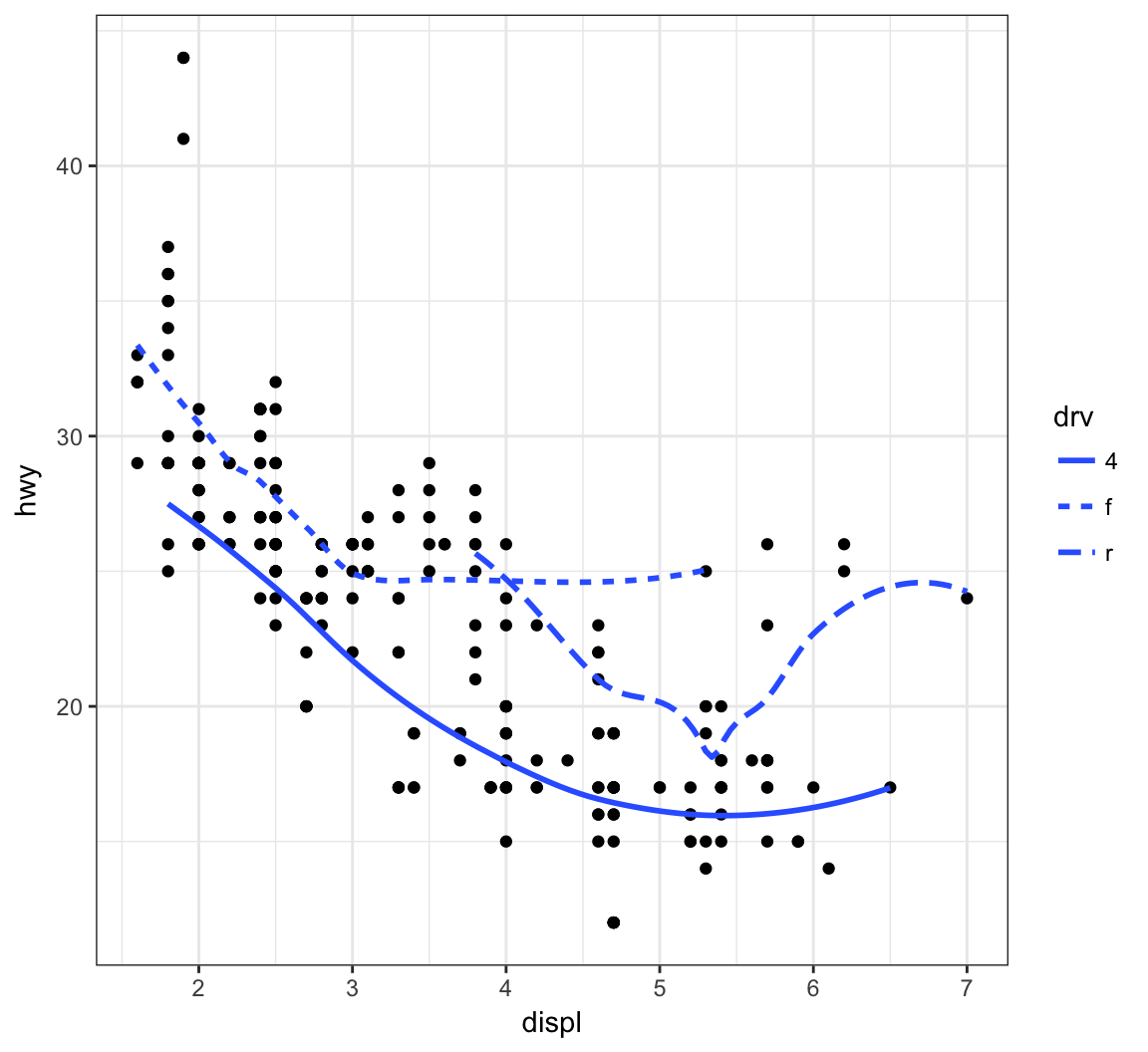
Instead of different line types, let’s instead differentiate them by line color:
> ggplot(data = mpg, mapping = aes(x = displ, y = hwy,
+ color=drv)) +
+ geom_point() +
+ geom_smooth(se=FALSE)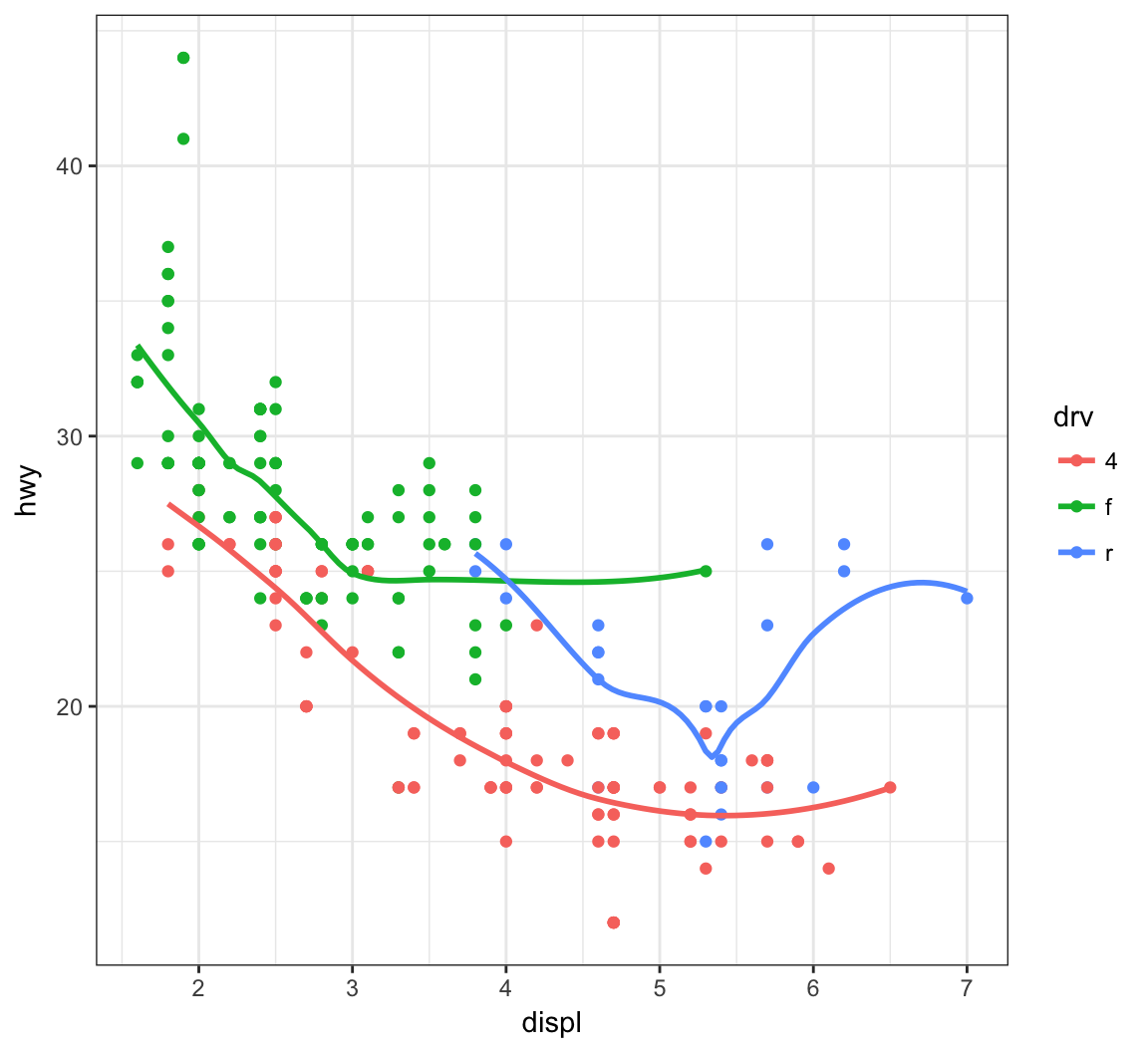
Overplotting
Definition
- Overplotting occurs when there are many observations, resulting in many objects being plotted on top of each other
- For example, the
diamondsdata set has 53940 observations per variable - Let’s explore some ways to deal with overplotting
Here is an example of an overplotted scatterplot:
> ggplot(data = diamonds, mapping = aes(x=carat, y=price)) +
+ geom_point()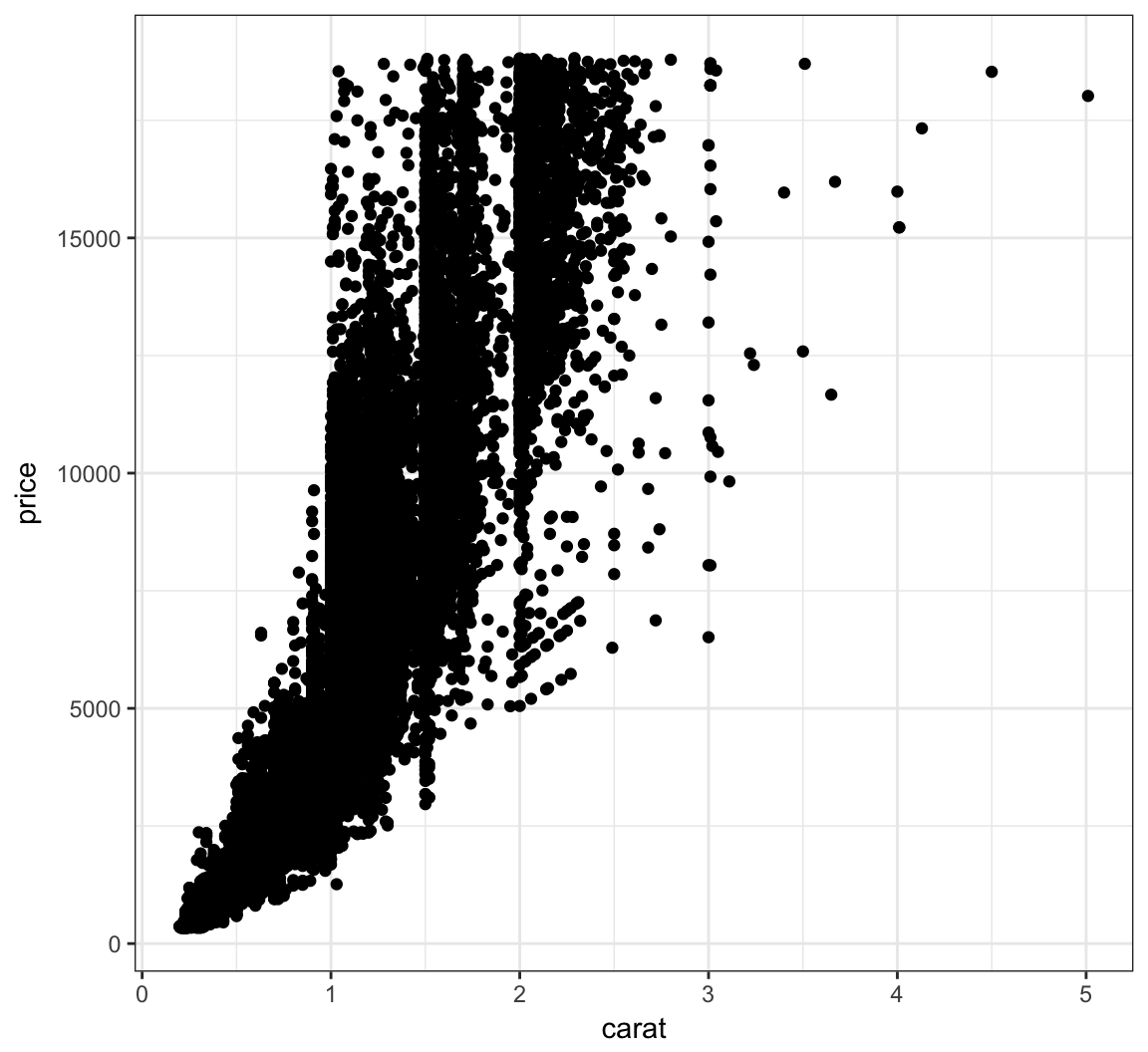
Let’s reduce the alpha of the points:
> ggplot(data = diamonds, mapping = aes(x=carat, y=price)) +
+ geom_point(alpha=0.1)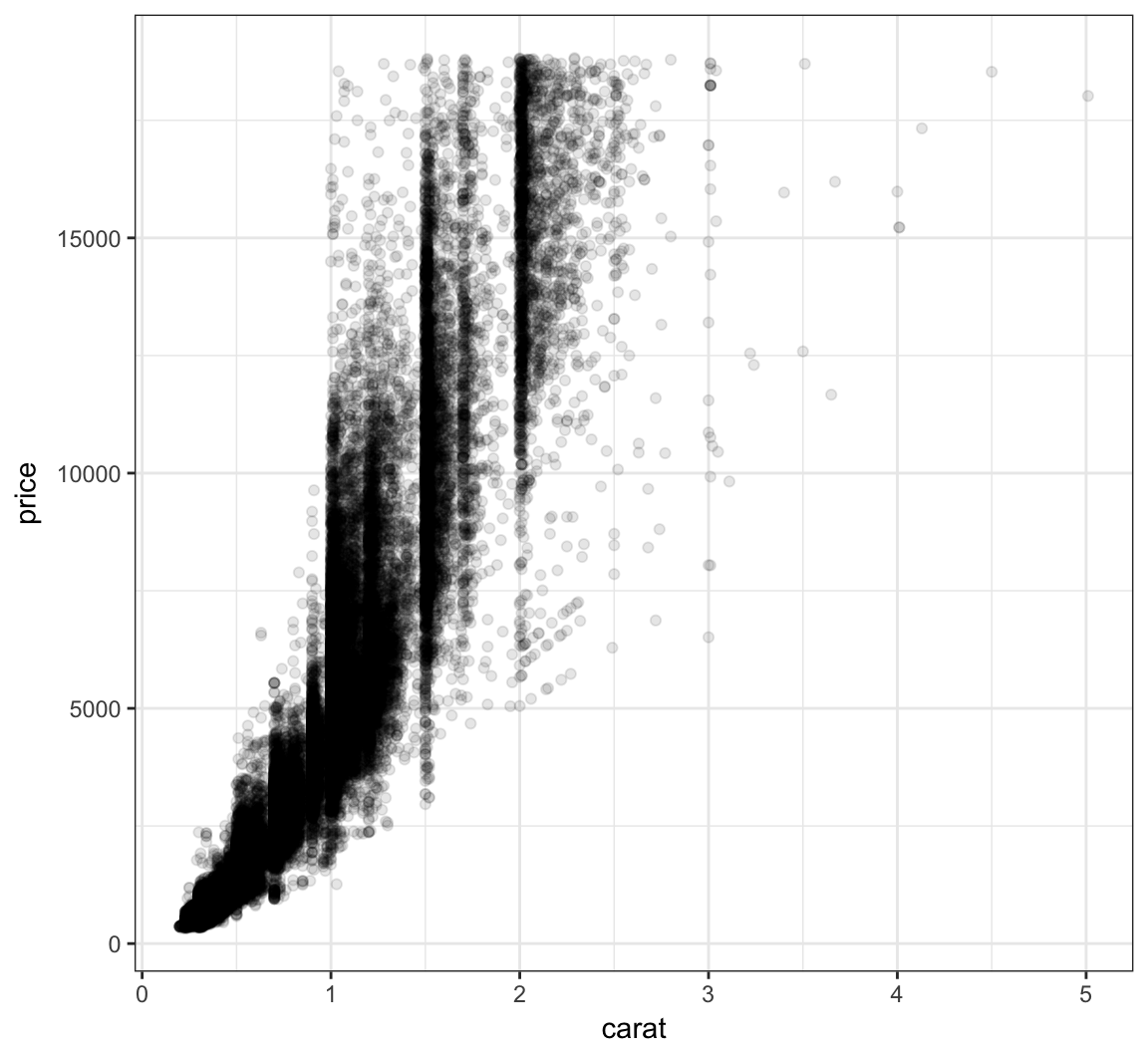
Let’s further reduce the alpha:
> ggplot(data = diamonds, mapping = aes(x=carat, y=price)) +
+ geom_point(alpha=0.01)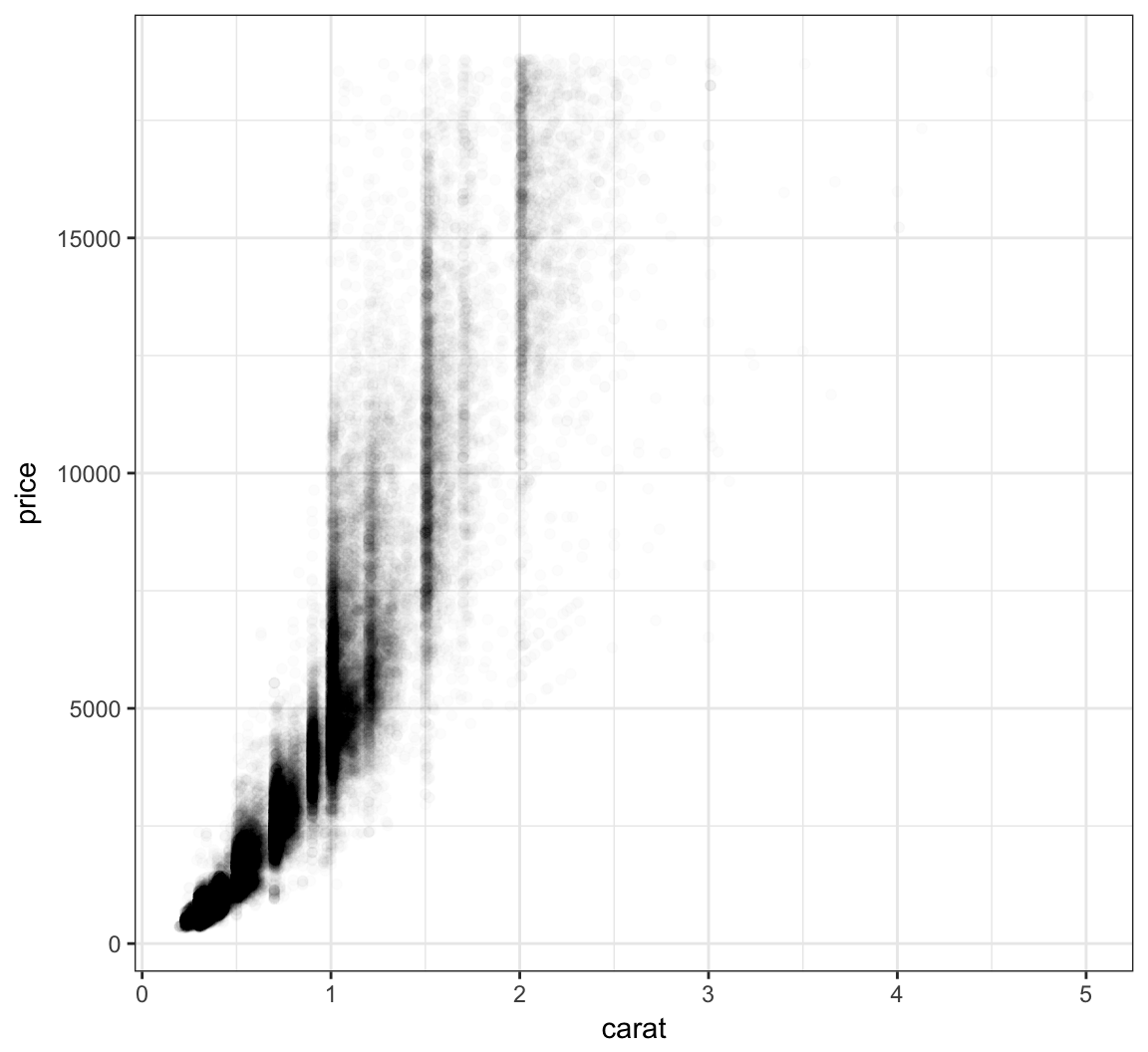
We can bin the points into hexagons, and report how many points fall within each bin. We use the geom_hex() layer to do this:
> ggplot(data = diamonds, mapping = aes(x=carat, y=price)) +
+ geom_hex()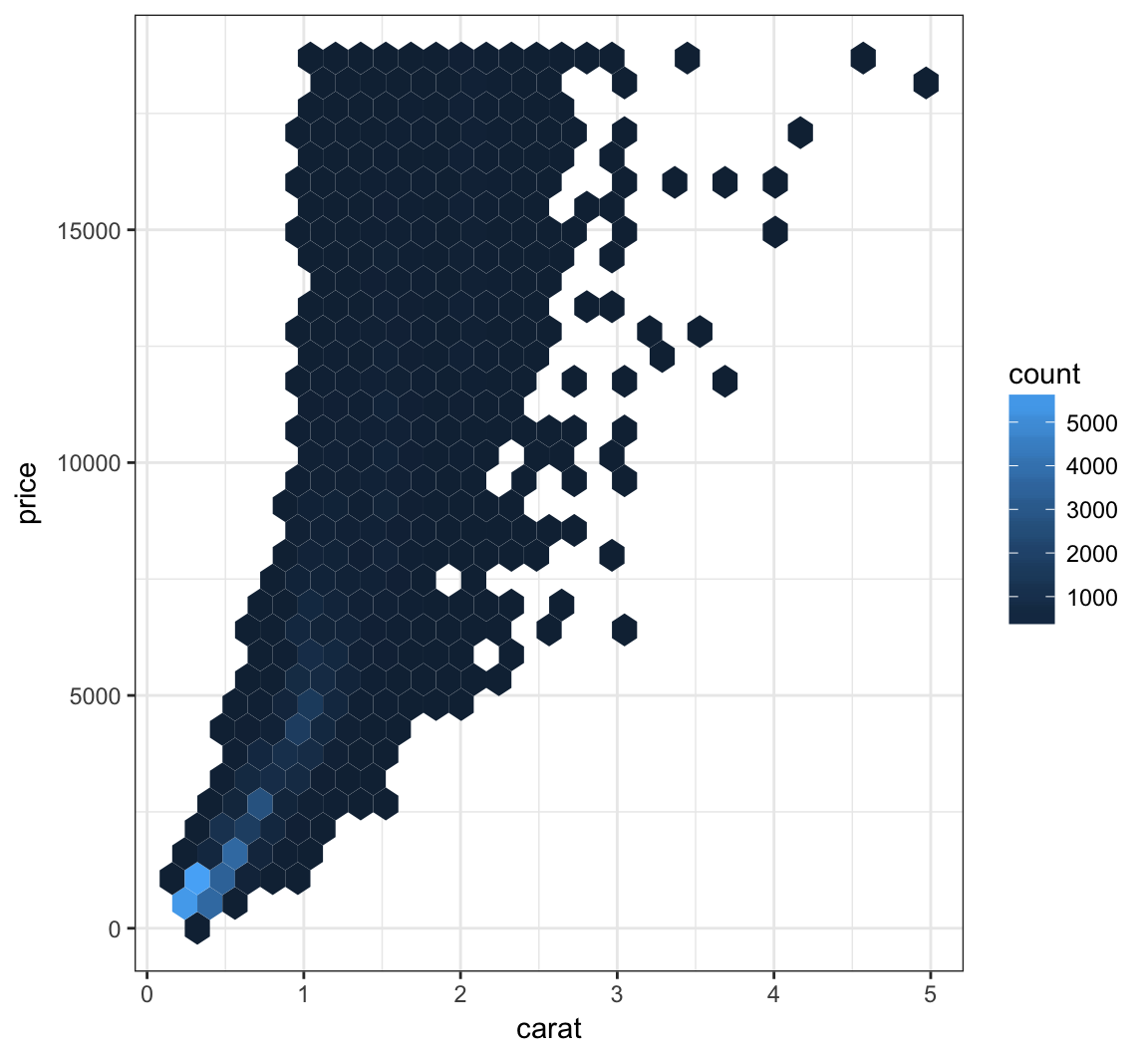
Let’s try to improve the color scheme:
> ggplot(data = diamonds, mapping = aes(x=carat, y=price)) +
+ geom_hex() +
+ scale_fill_gradient2(low="lightblue", mid="purple", high="black",
+ midpoint=3000)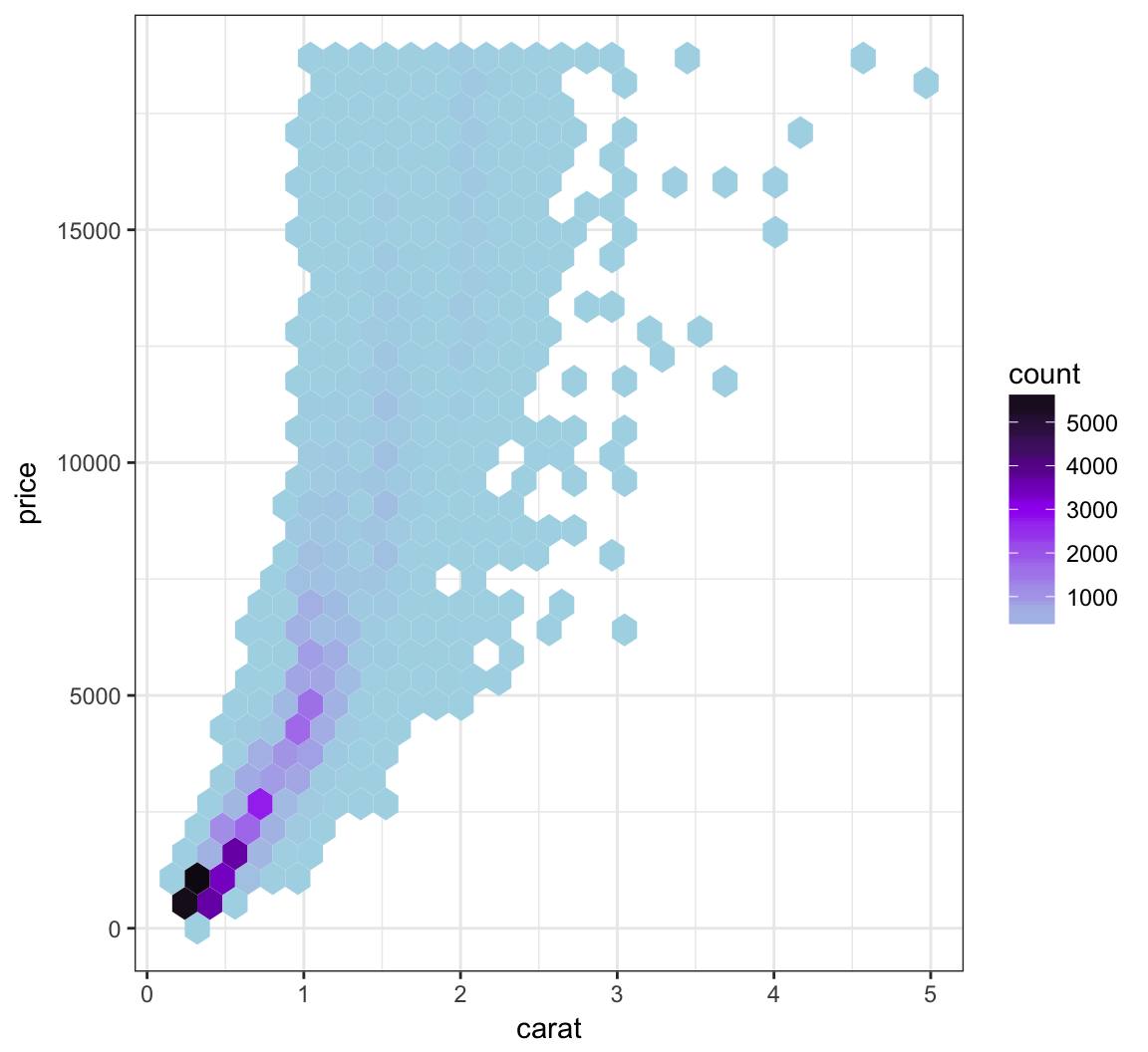
We can combine the scale transformation used earlier with the “hexbin” plotting method:
> ggplot(data = diamonds, mapping = aes(x=carat, y=price)) +
+ geom_hex(bins=20) +
+ scale_x_log10(breaks=1:5) + scale_y_log10(breaks=c(1000,5000,10000)) 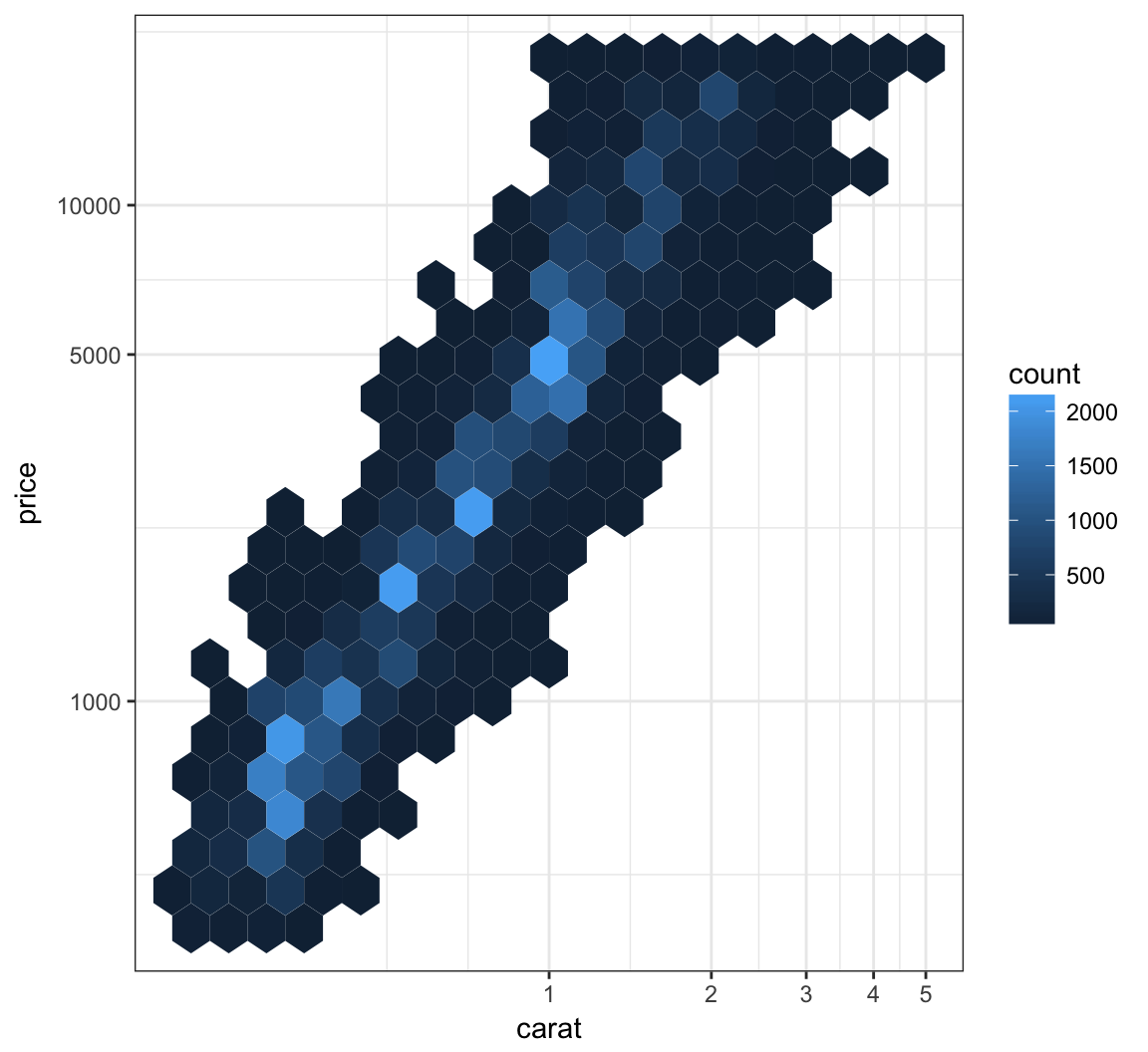
Labels and Legends
Here’s how you can change the axis labels and give the plot a title:
> ggplot(data = mpg) +
+ geom_boxplot(mapping = aes(x = factor(cyl), y = hwy)) +
+ labs(title="Highway MPG by Cylinders",x="Cylinders",
+ y="Highway MPG")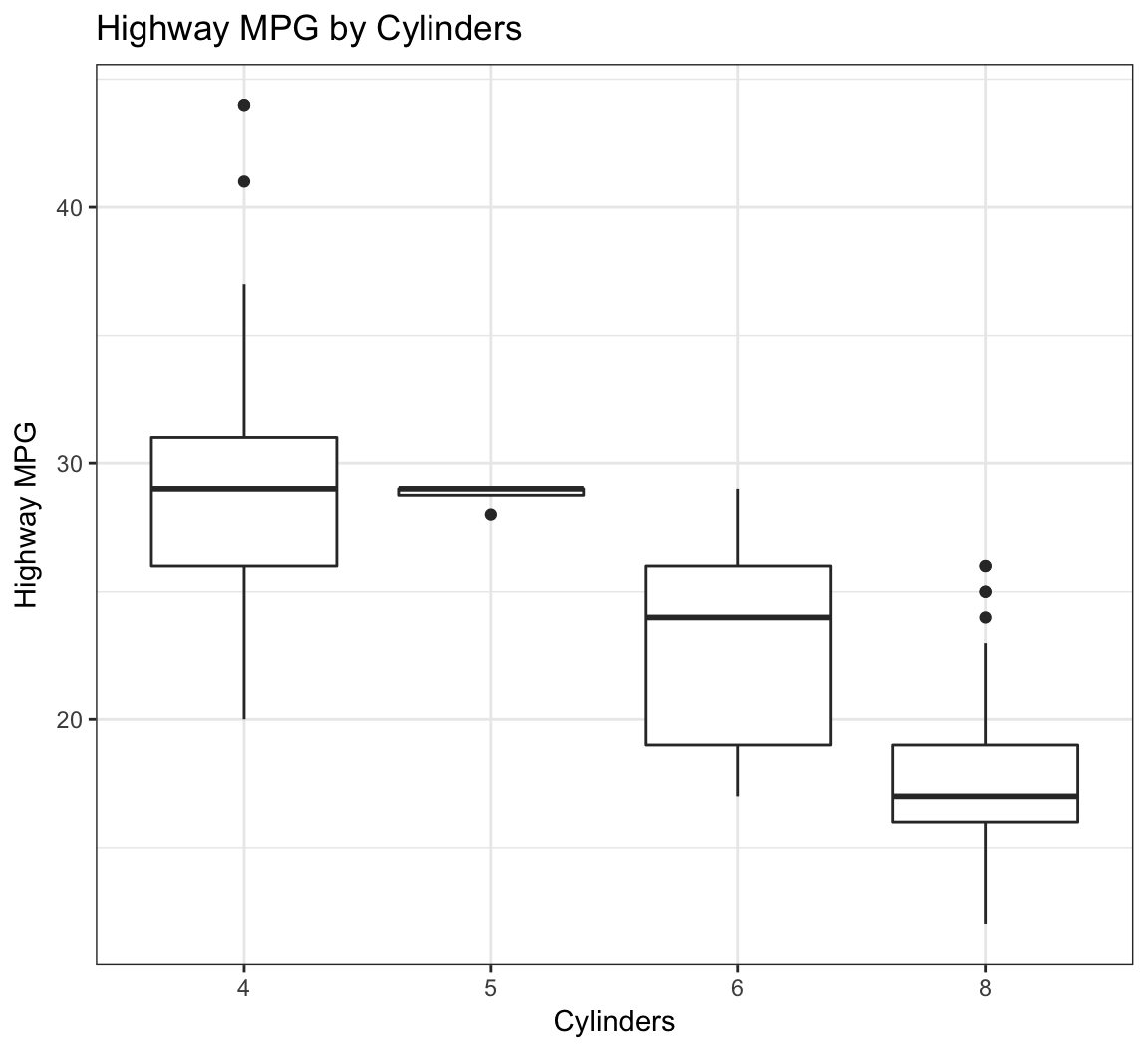
You can remove the legend to a plot by the following:
> ggplot(data = diamonds) +
+ geom_bar(mapping = aes(x = cut, fill = cut)) +
+ theme(legend.position="none")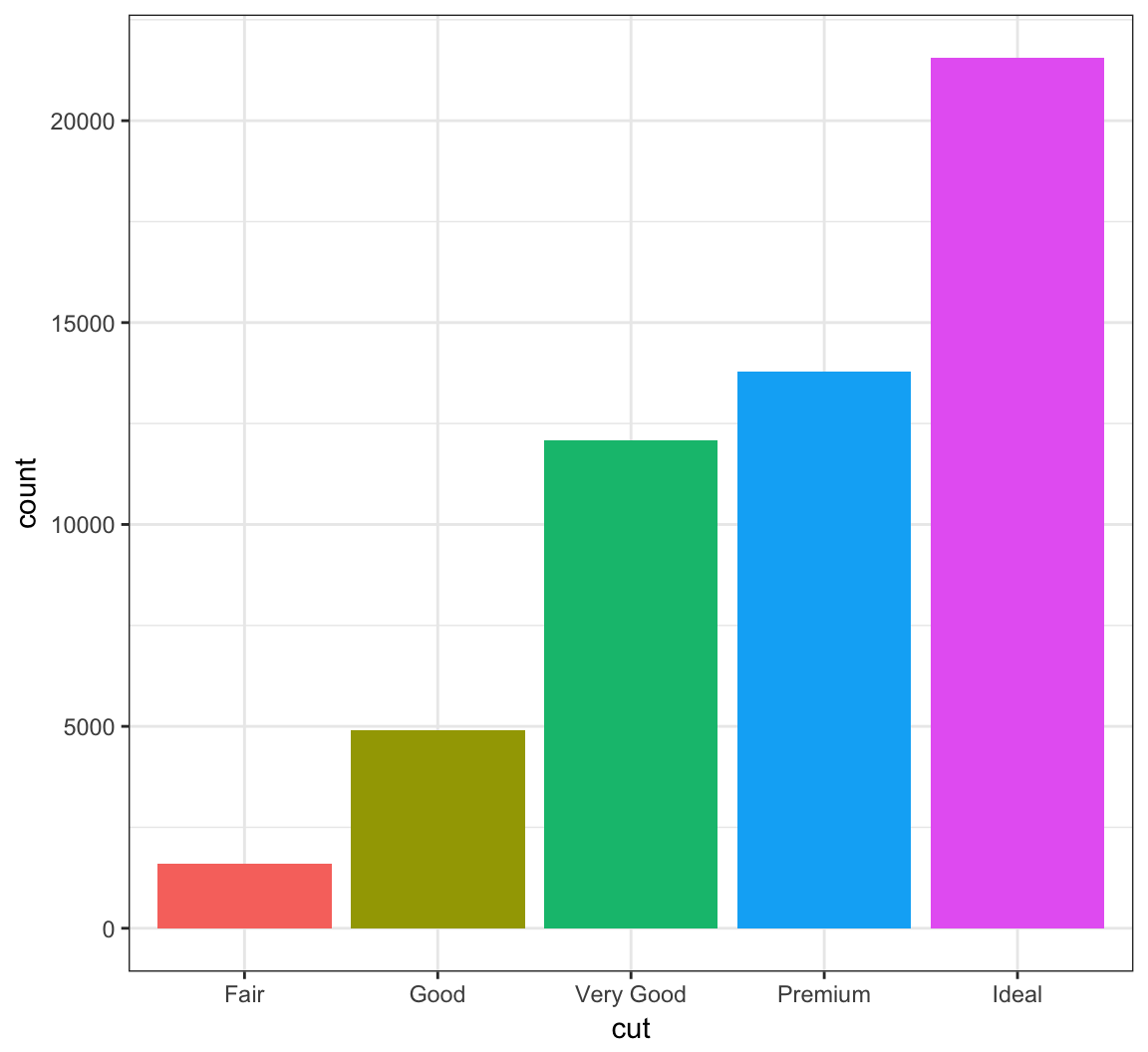
The legend can be placed on the “top”, “bottom”, “left”, or “right”:
> ggplot(data = diamonds) +
+ geom_bar(mapping = aes(x = cut, fill = cut)) +
+ theme(legend.position="bottom")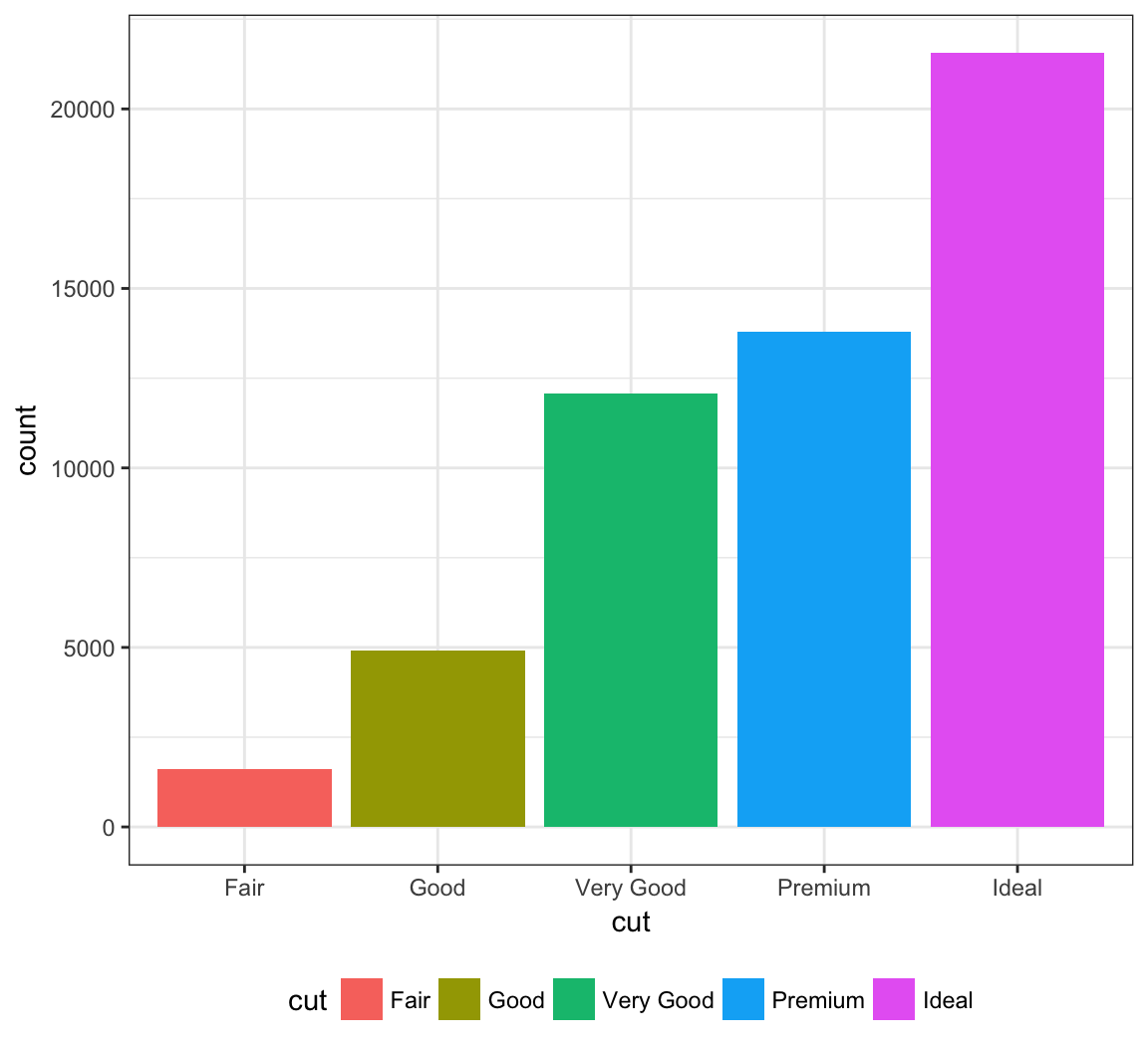
The legend can be moved inside the plot itself:
> ggplot(data = diamonds) +
+ geom_bar(mapping = aes(x = cut, fill = cut)) +
+ theme(legend.position=c(0.15,0.75))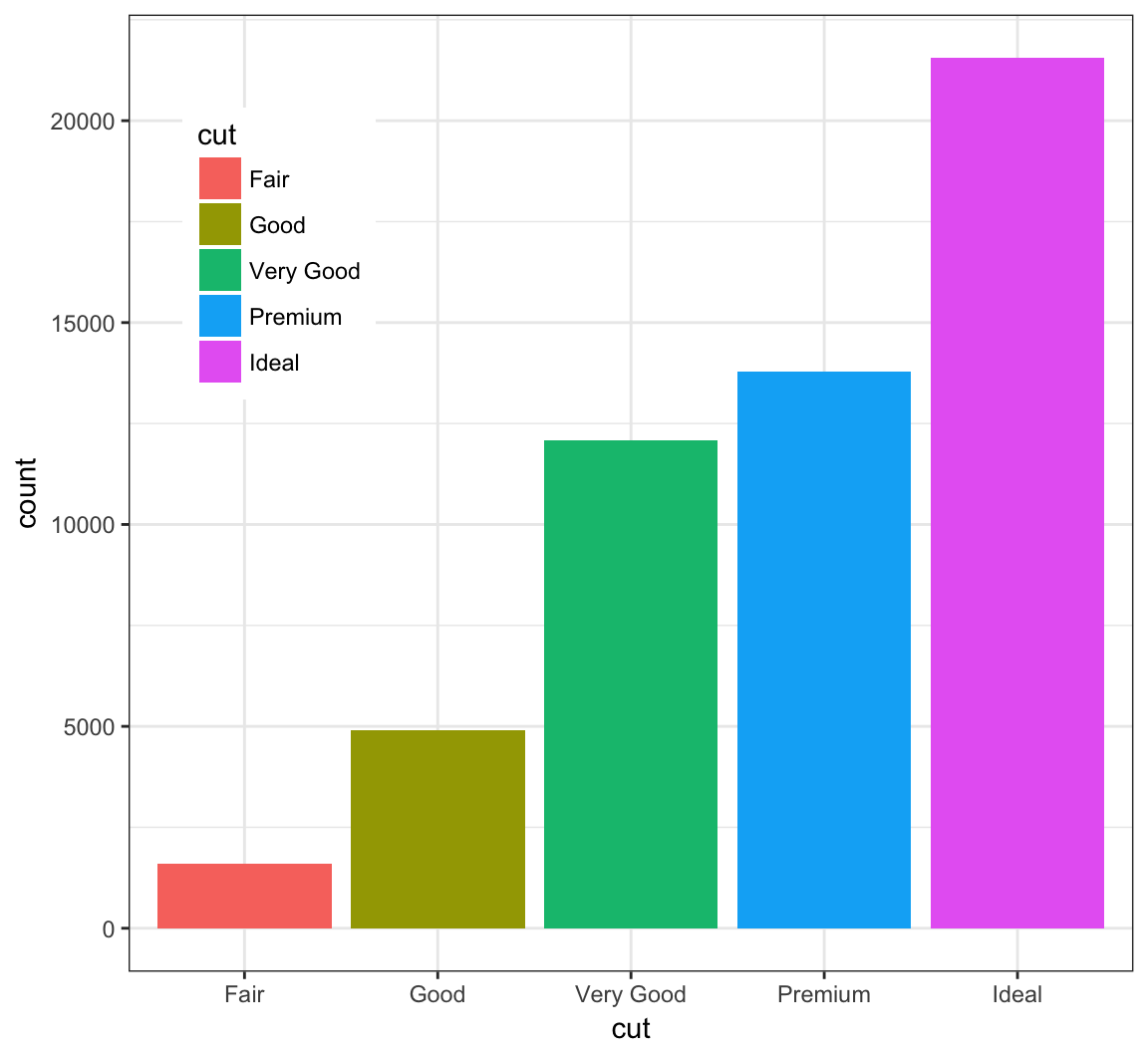
Change the name of the legend:
> ggplot(data = diamonds) +
+ geom_bar(mapping = aes(x = cut, fill = cut)) +
+ scale_fill_discrete(name="Diamond\nCut")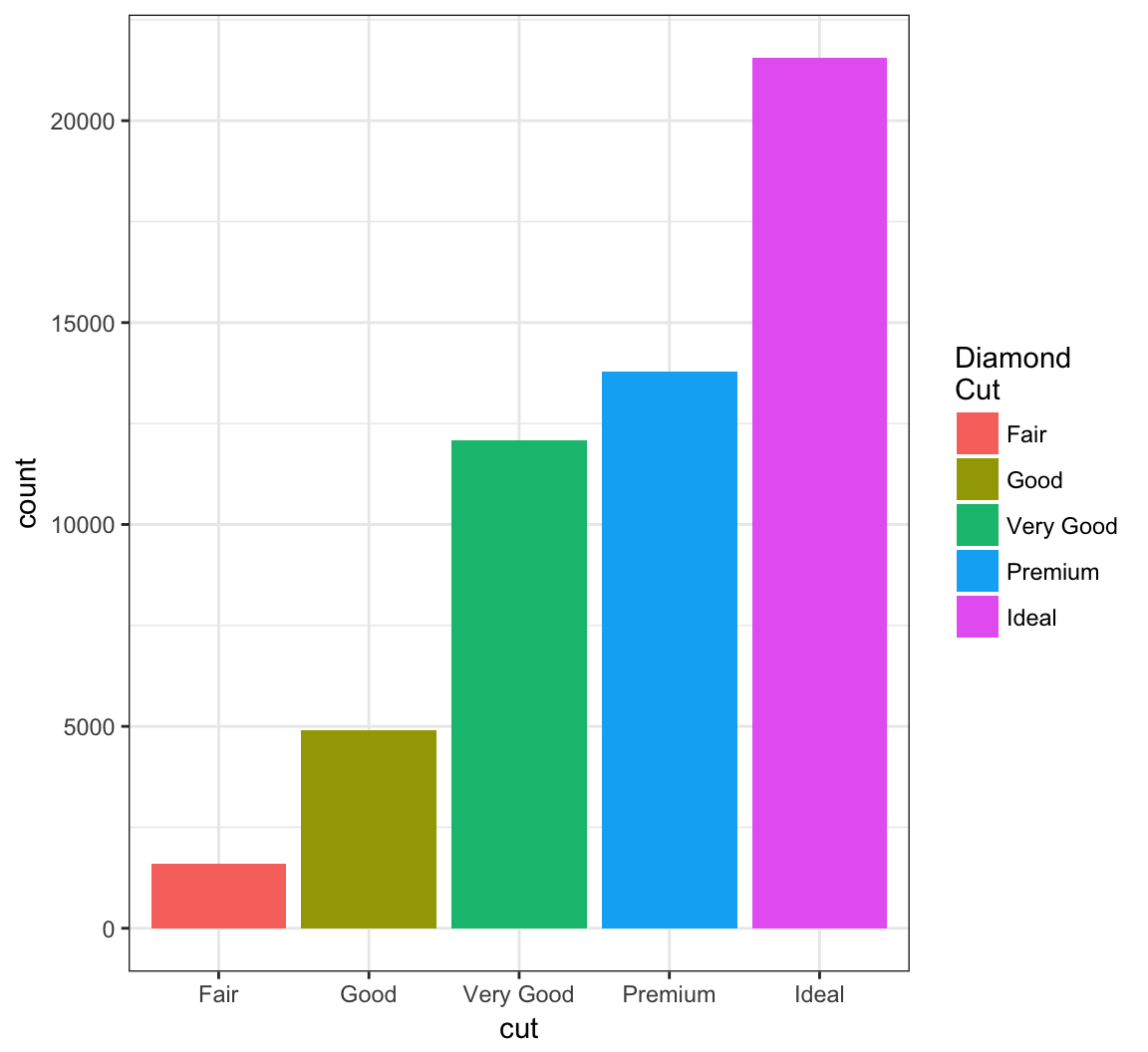
Change the labels within the legend:
> ggplot(data = diamonds) +
+ geom_bar(mapping = aes(x = cut, fill = cut)) +
+ scale_fill_discrete(labels=c("F", "G", "VG", "P", "I"))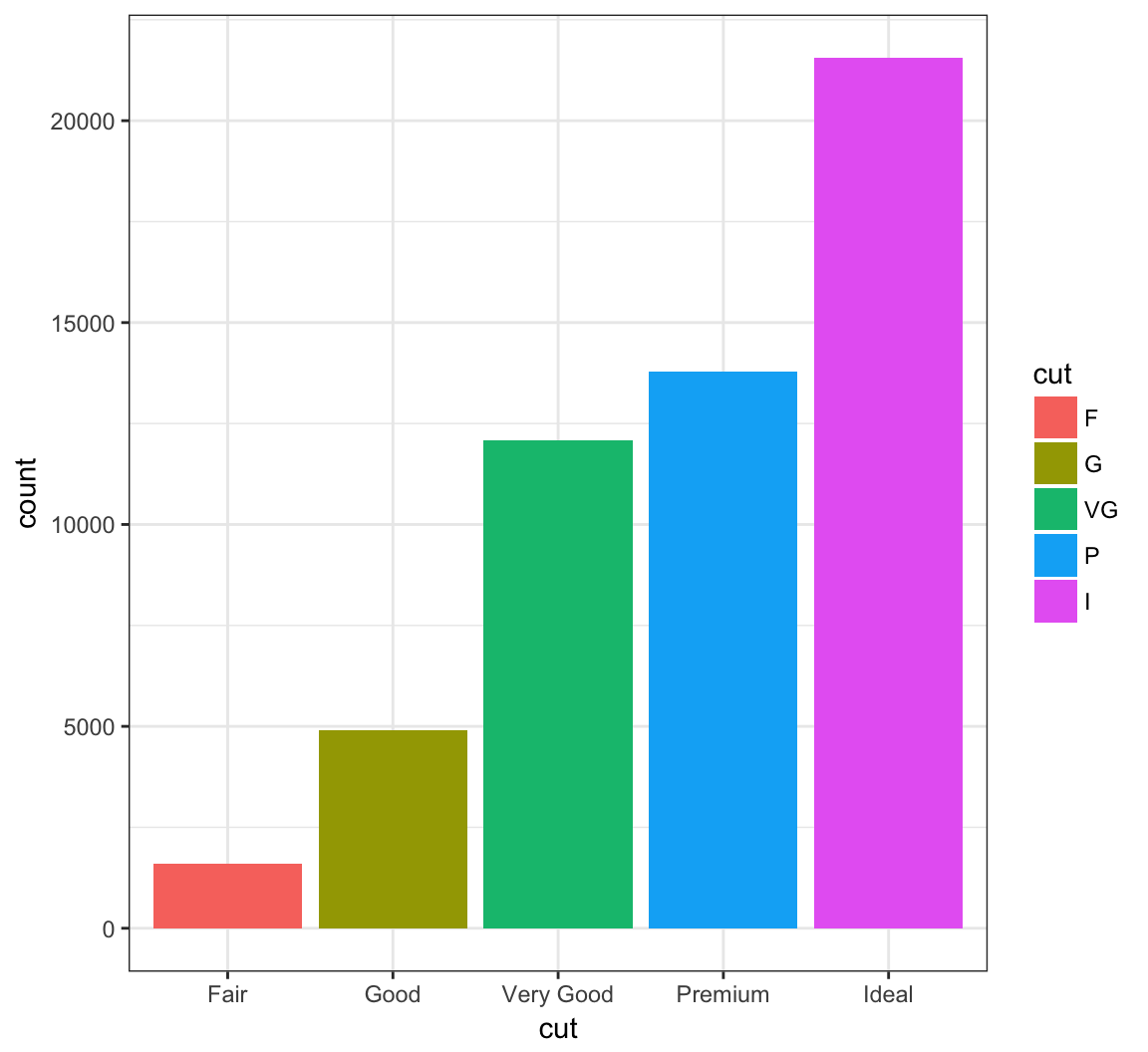
Facets
Here is the histogram of the displ variable from the mpg data set:
> ggplot(mpg) + geom_histogram(mapping=aes(x=displ),
+ binwidth=0.25)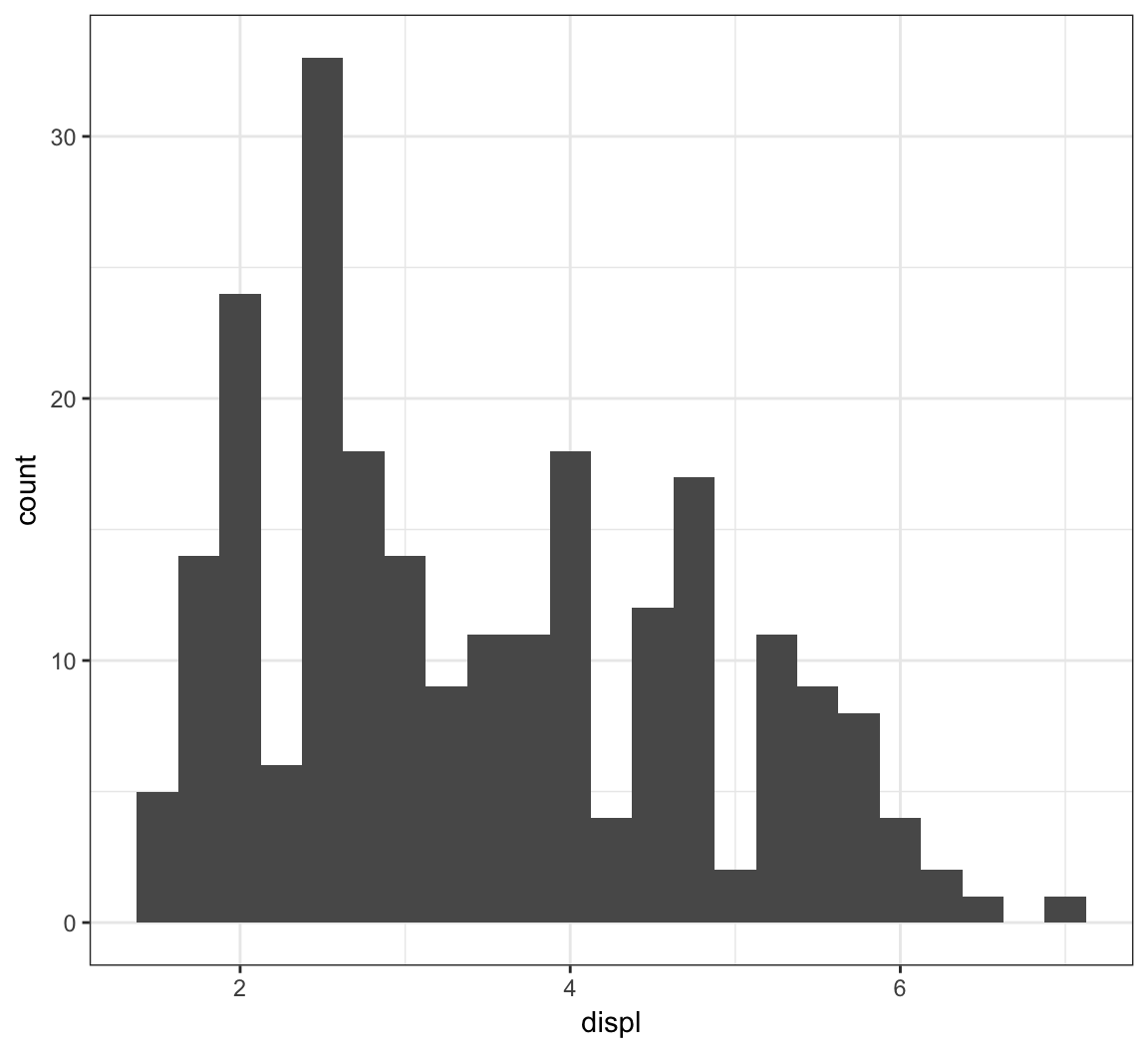
The facet_wrap() layer allows us to stratify the displ variable according to cyl, and show the histograms for the strata in an organized fashion:
> ggplot(mpg) +
+ geom_histogram(mapping=aes(x=displ), binwidth=0.25) +
+ facet_wrap(~ cyl)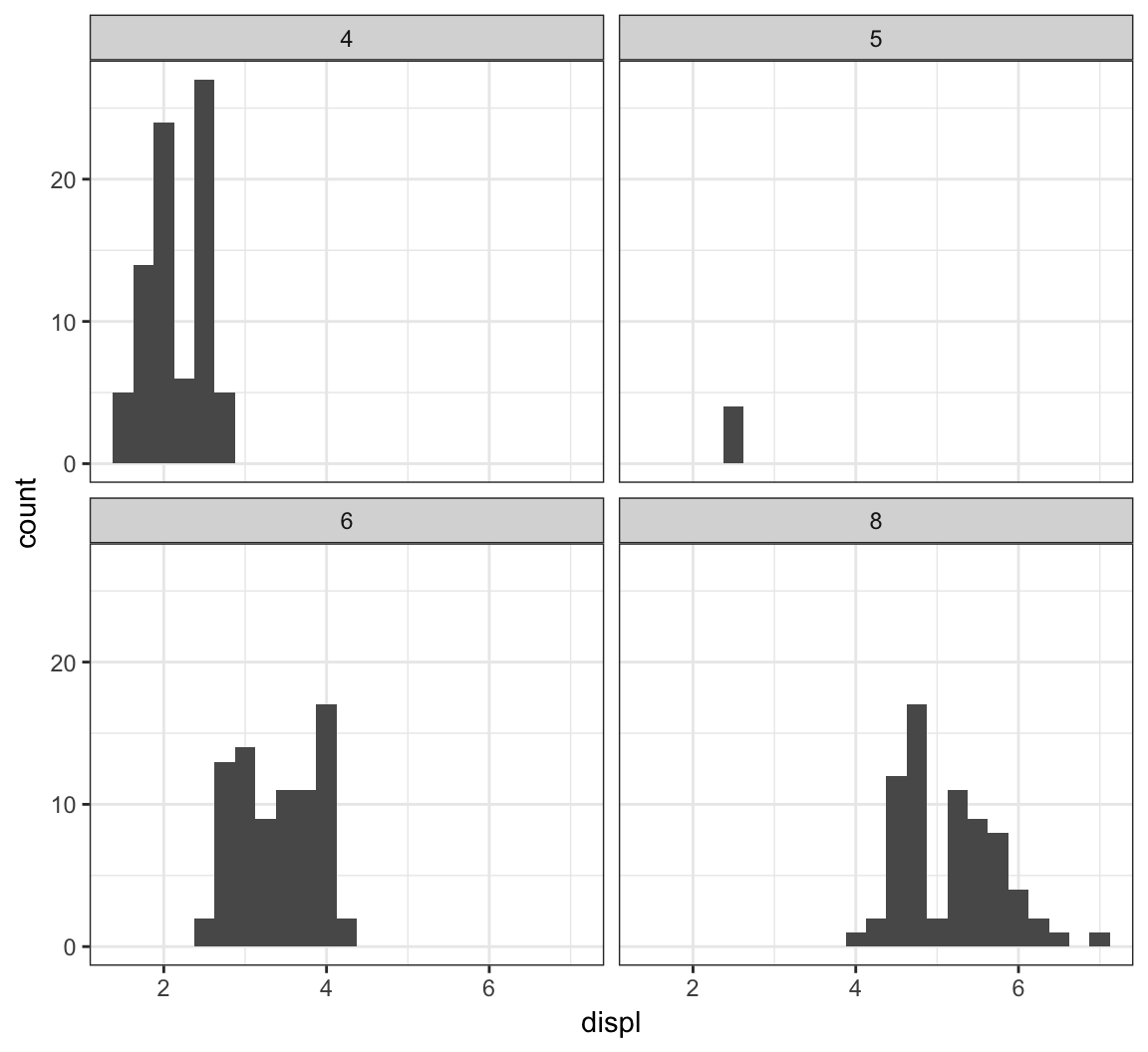
Here is facet_wrap() applied to displ startified by the drv variable:
> ggplot(mpg) +
+ geom_histogram(mapping=aes(x=displ), binwidth=0.25) +
+ facet_wrap(~ drv)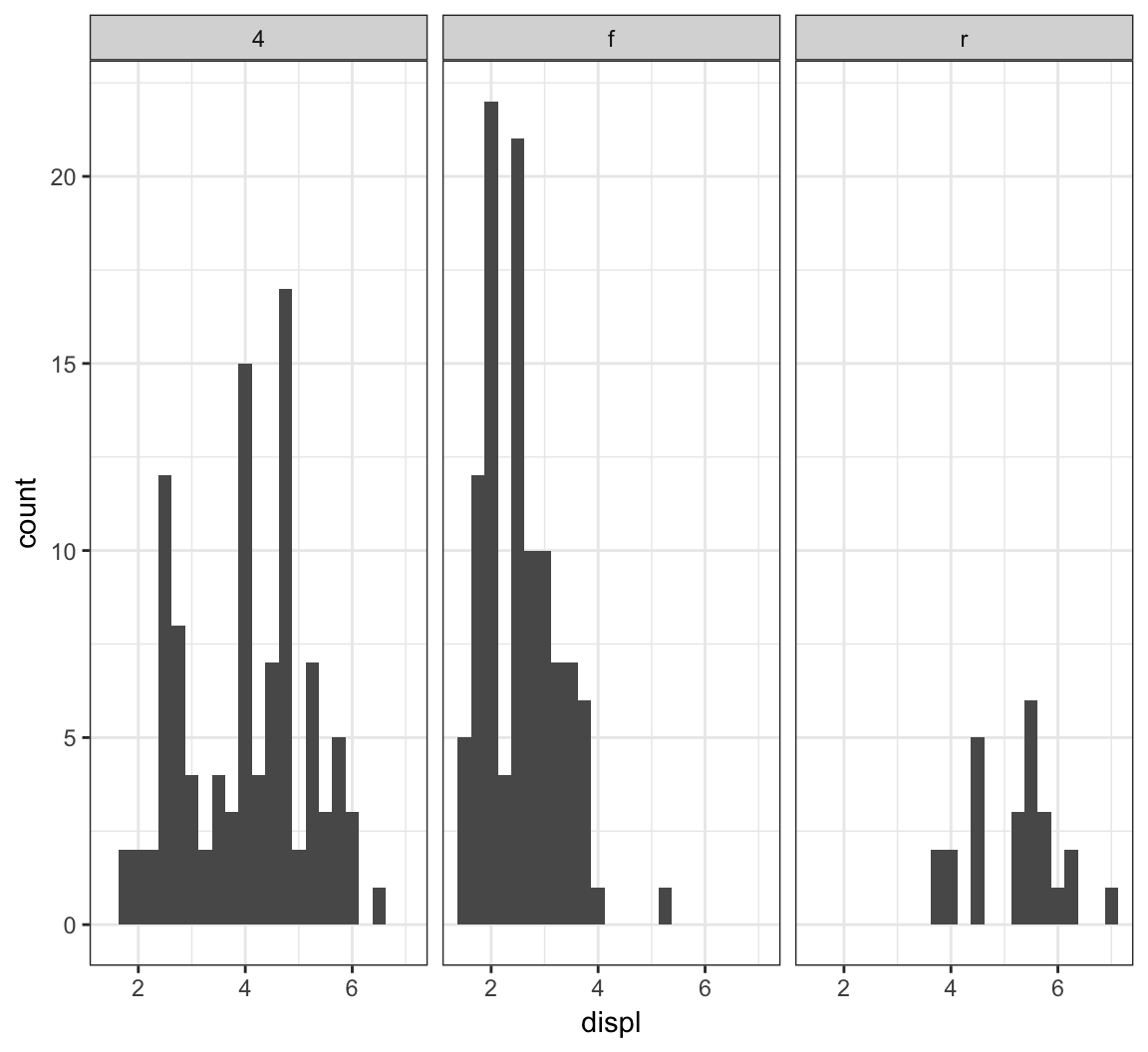
We can stratify by two variable simultaneously by using the facet_grid() layer:
> ggplot(mpg) +
+ geom_histogram(mapping=aes(x=displ), binwidth=0.25) +
+ facet_grid(drv ~ cyl)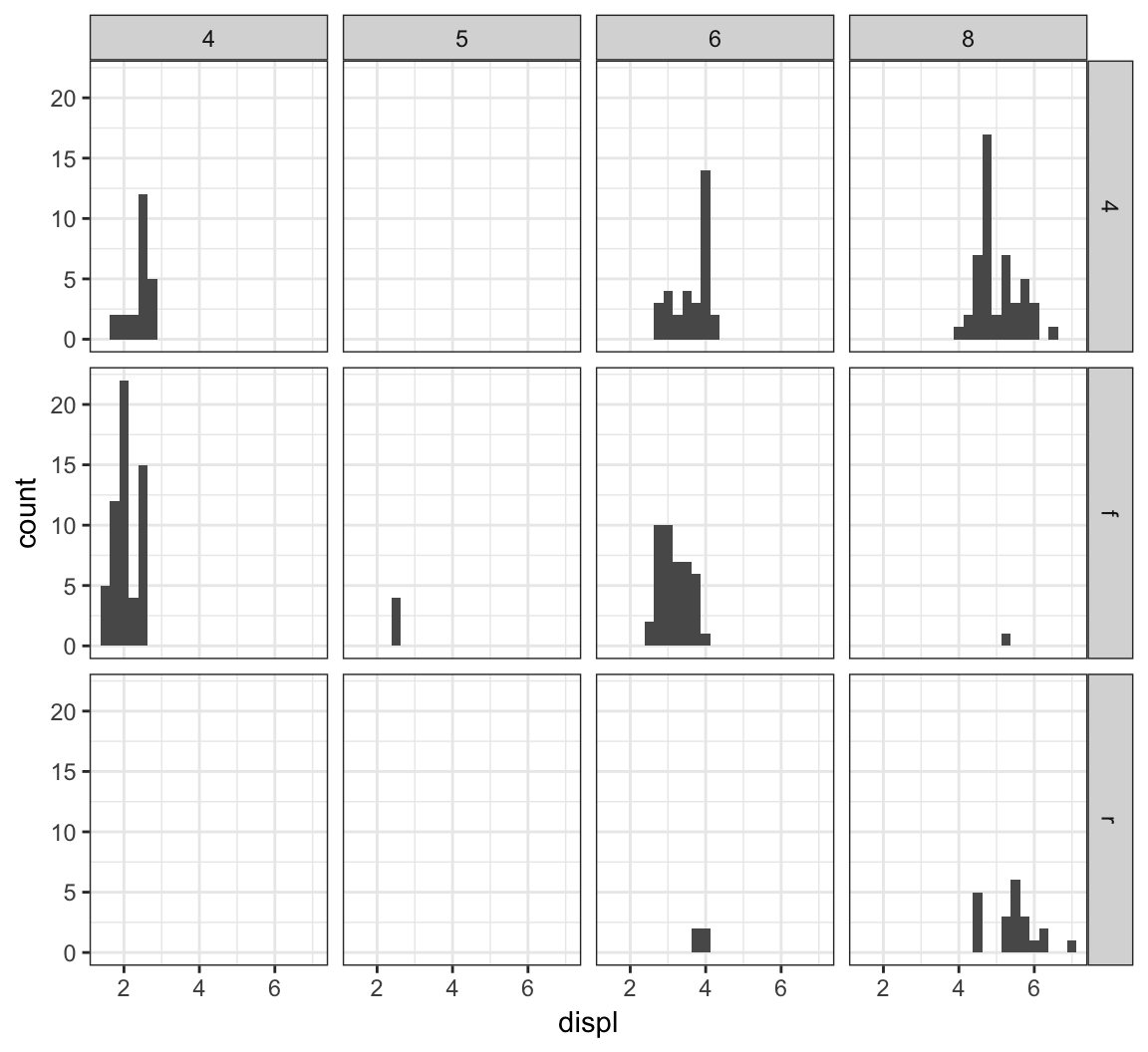
Let’s carry out a similar faceting on the diamonds data over the next four plots:
> ggplot(diamonds) +
+ geom_histogram(mapping=aes(x=price), binwidth=500)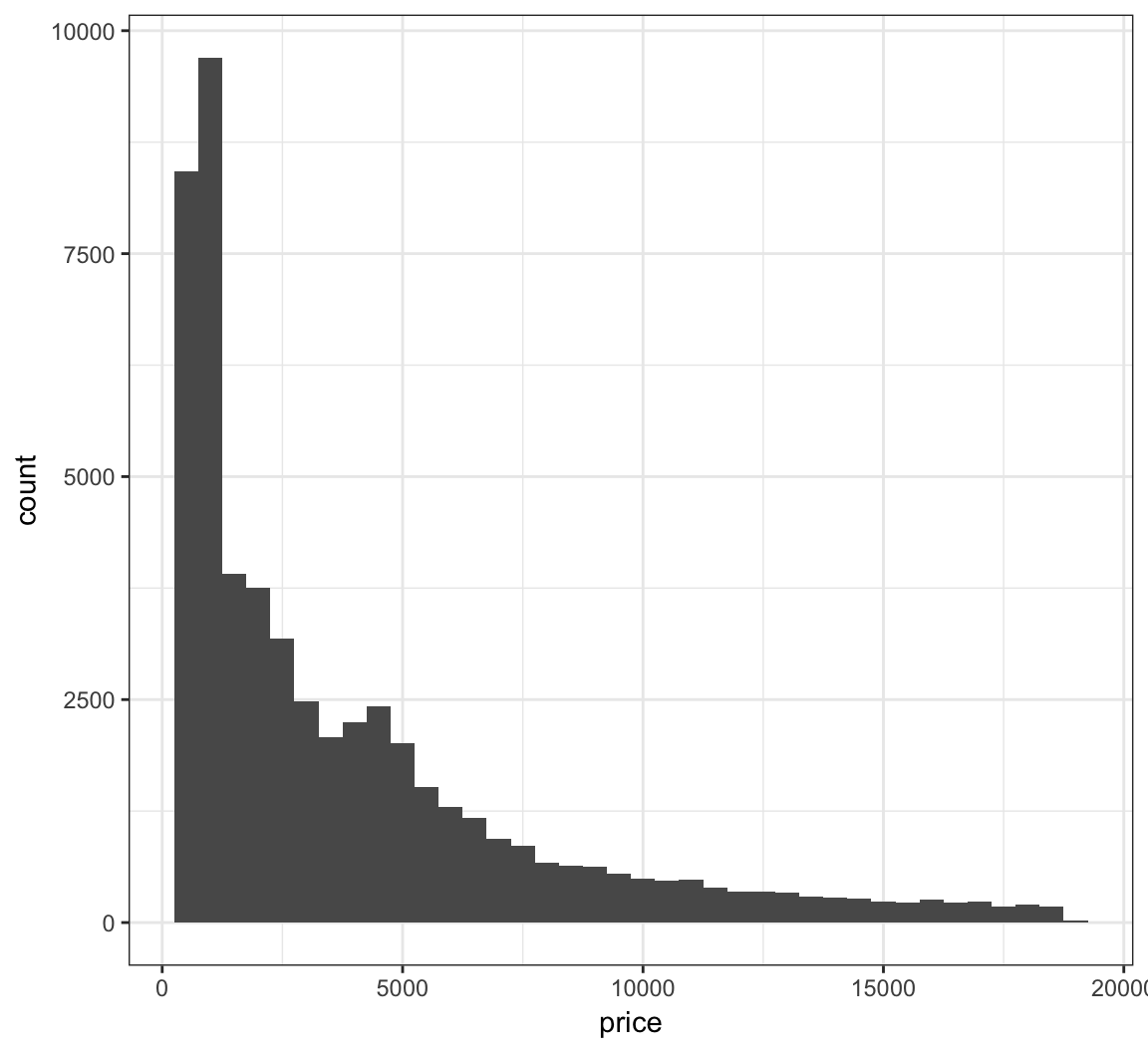
Stratify price by clarity:
> ggplot(diamonds) +
+ geom_histogram(mapping=aes(x=price), binwidth=500) +
+ facet_wrap(~ clarity)
Stratify price by clarity, but allow each y-axis range to be different by including the scale="free_y" argument:
> ggplot(diamonds) +
+ geom_histogram(mapping=aes(x=price), binwidth=500) +
+ facet_wrap(~ clarity, scale="free_y")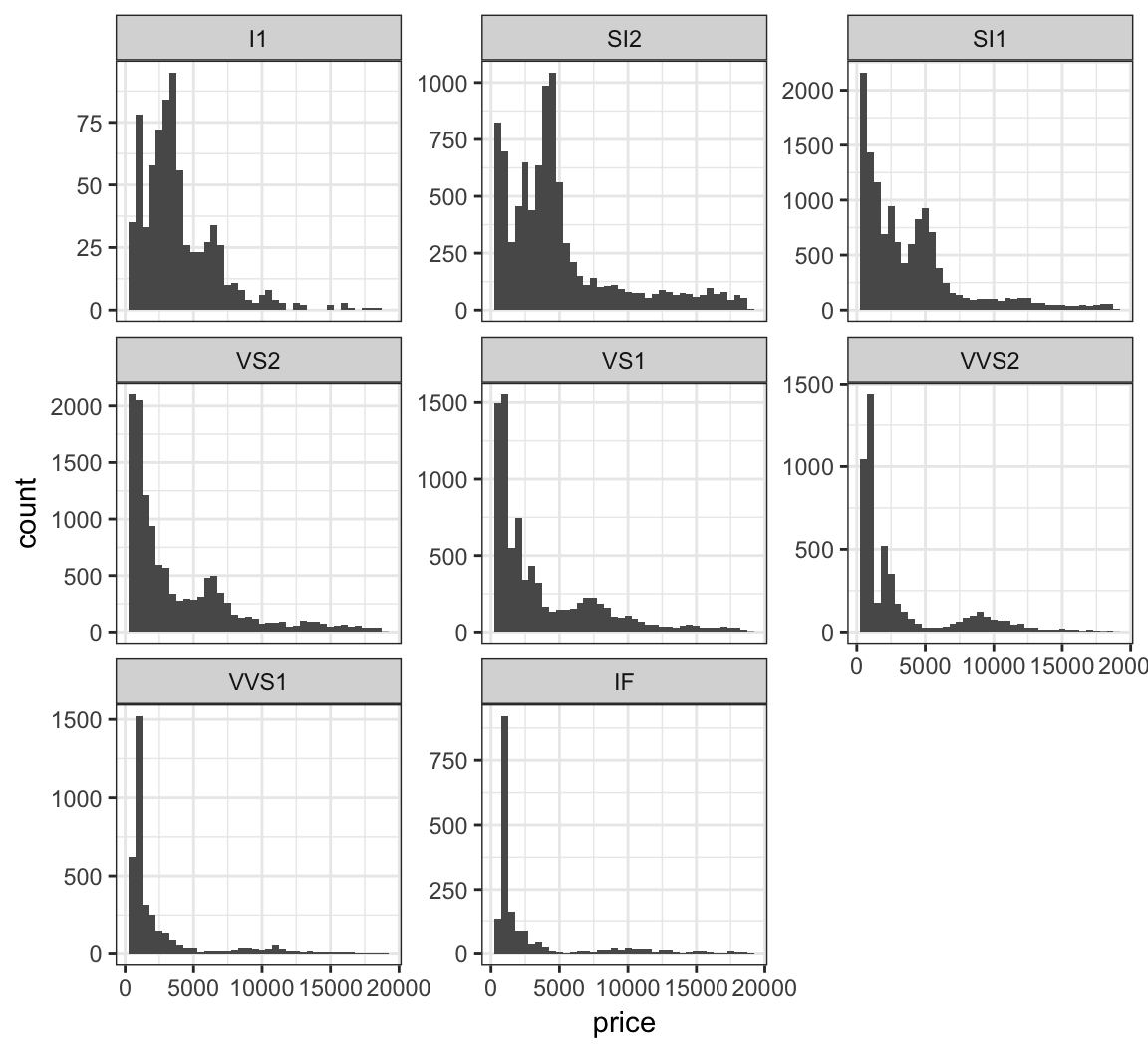
Jointly stratify price by cut and clarify:
> ggplot(diamonds) +
+ geom_histogram(mapping=aes(x=price), binwidth=500) +
+ facet_grid(cut ~ clarity) +
+ scale_x_continuous(breaks=9000)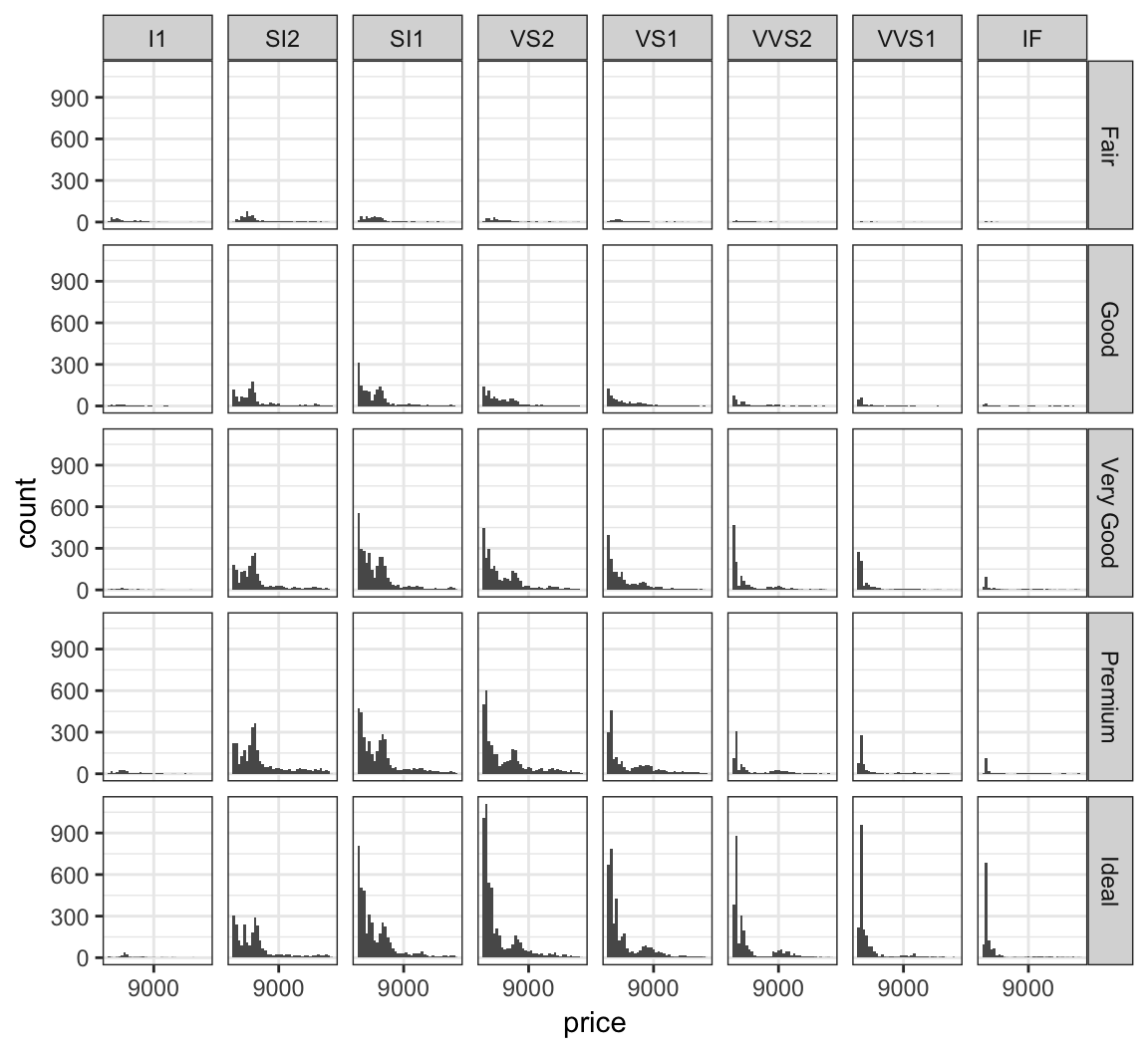
Colors
Finding Colors
- A list of named colors in R (e.g., “lightblue”)
- RColorBrewer package
- The Crayola crayon colors from the
bromanpackage – usebrocolors(set="crayons") - Color blind palette:
> cbPalette <- c("#999999", "#E69F00", "#56B4E9", "#009E73", "#F0E442", "#0072B2",
+ "#D55E00", "#CC79A7")Some Useful Layers
scale_fill_manual()scale_color_manual()scale_fill_gradient()scale_color_gradient()
Manually determine colors to fill the barplot using the color blind palette defined above, cbPalette:
> ggplot(data = diamonds) +
+ geom_bar(mapping = aes(x = cut, fill = cut)) +
+ scale_fill_manual(values=cbPalette)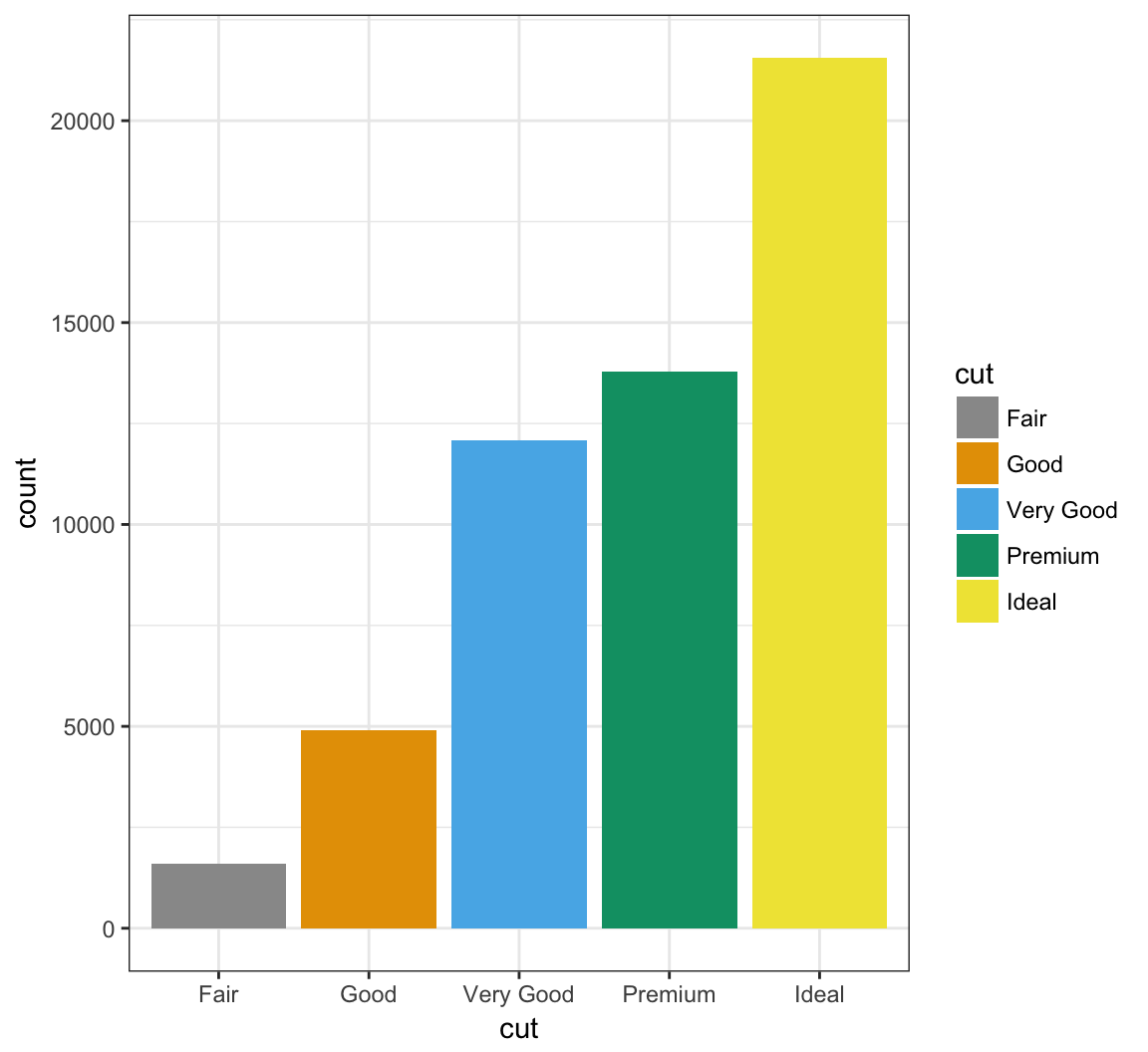
Manually determine point colors using the color blind palette defined above, cbPalette:
> ggplot(data = mpg) +
+ geom_point(mapping = aes(x = displ, y = hwy, color = class), size=2) +
+ scale_color_manual(values=cbPalette)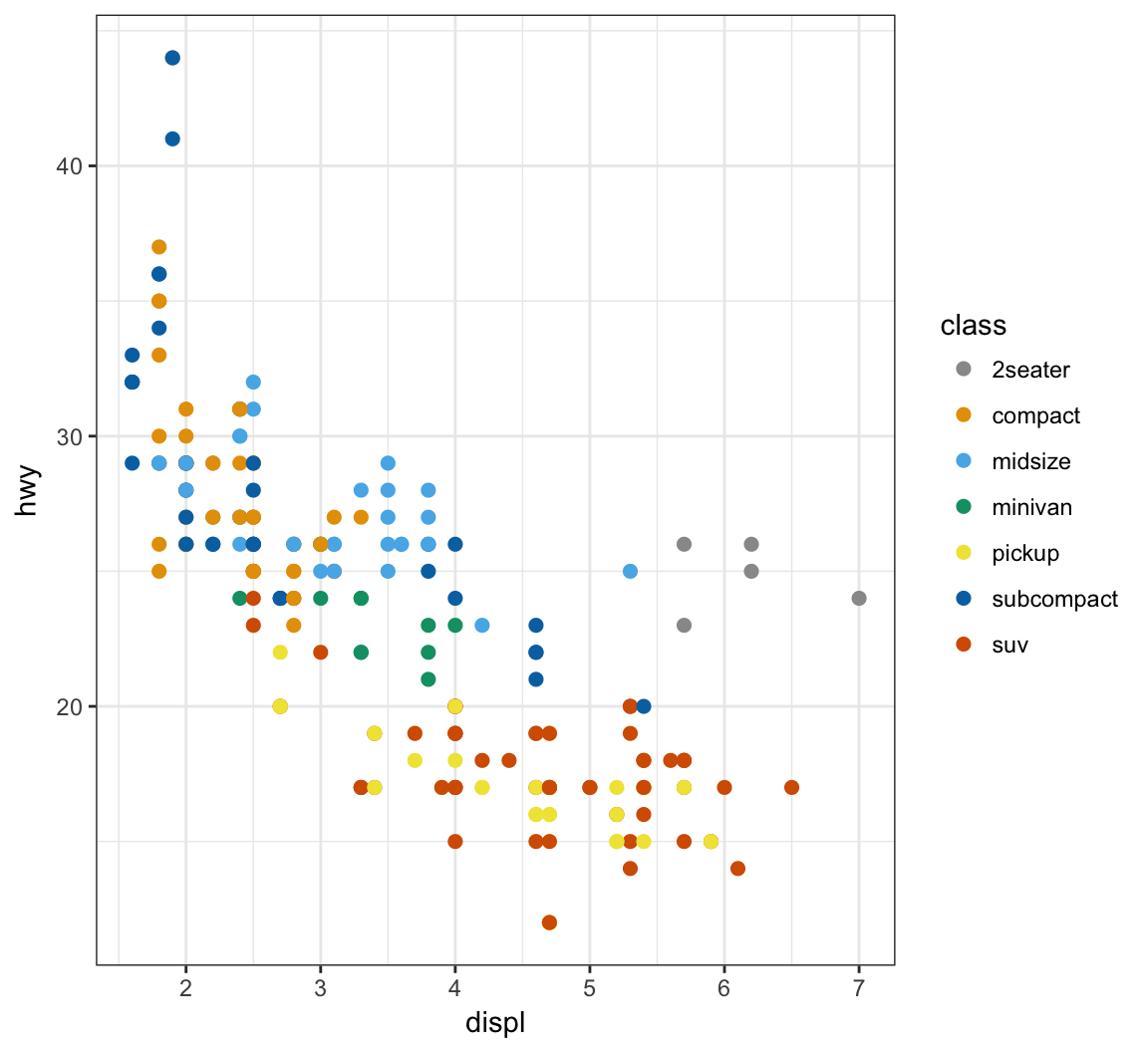
Fill the histogram bars using a color gradient by their counts, where we determine the endpoint colors:
> ggplot(data = mpg) +
+ geom_histogram(aes(x=hwy, fill=..count..)) +
+ scale_fill_gradient(low="blue", high="red")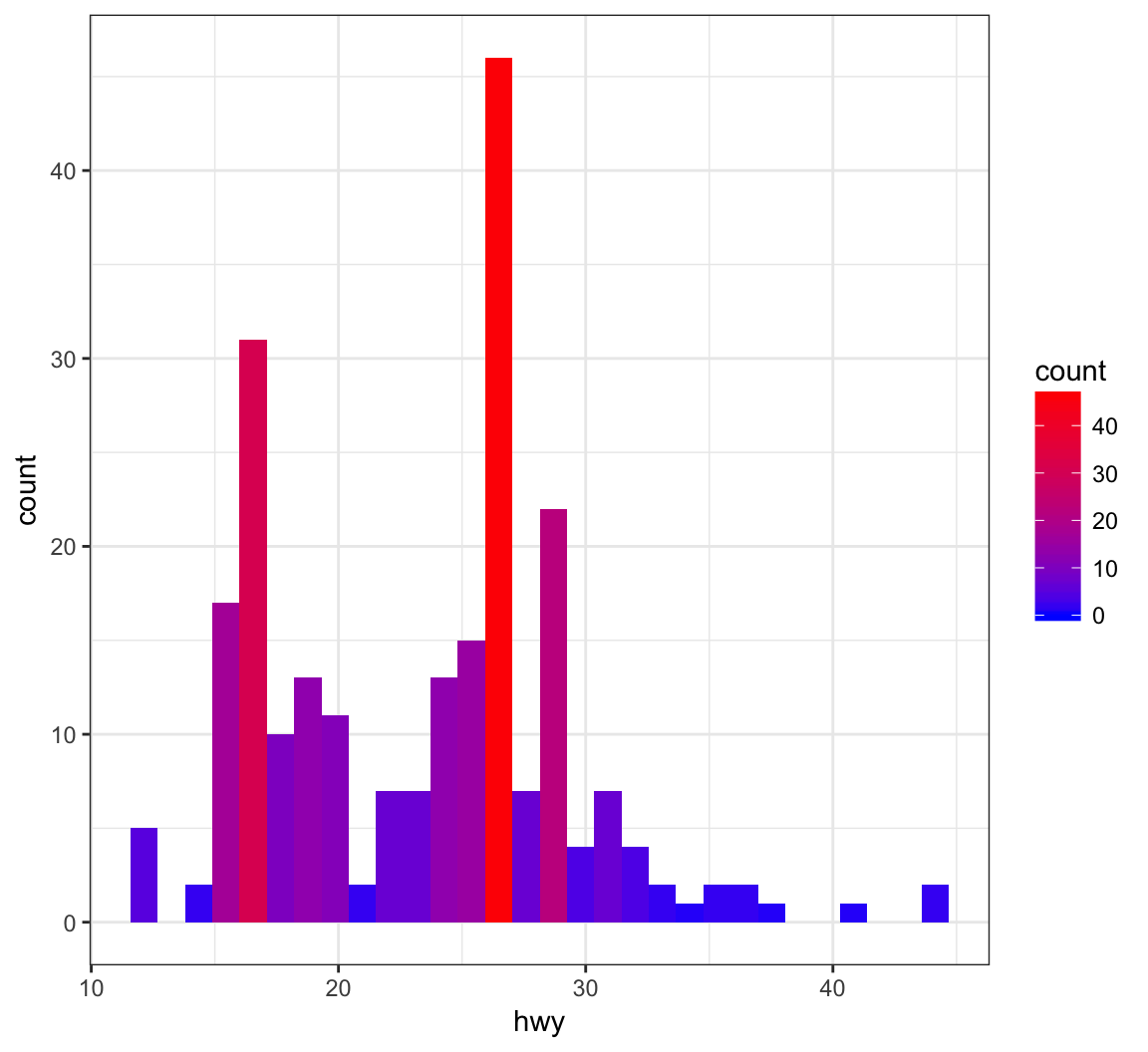
Color the points based on a gradient formed from the quantitative variable, displ, where we we determine the endpoint colors:
> ggplot(data = mpg) +
+ geom_point(aes(x=hwy, y=cty, color=displ), size=2) +
+ scale_color_gradient(low="blue", high="red")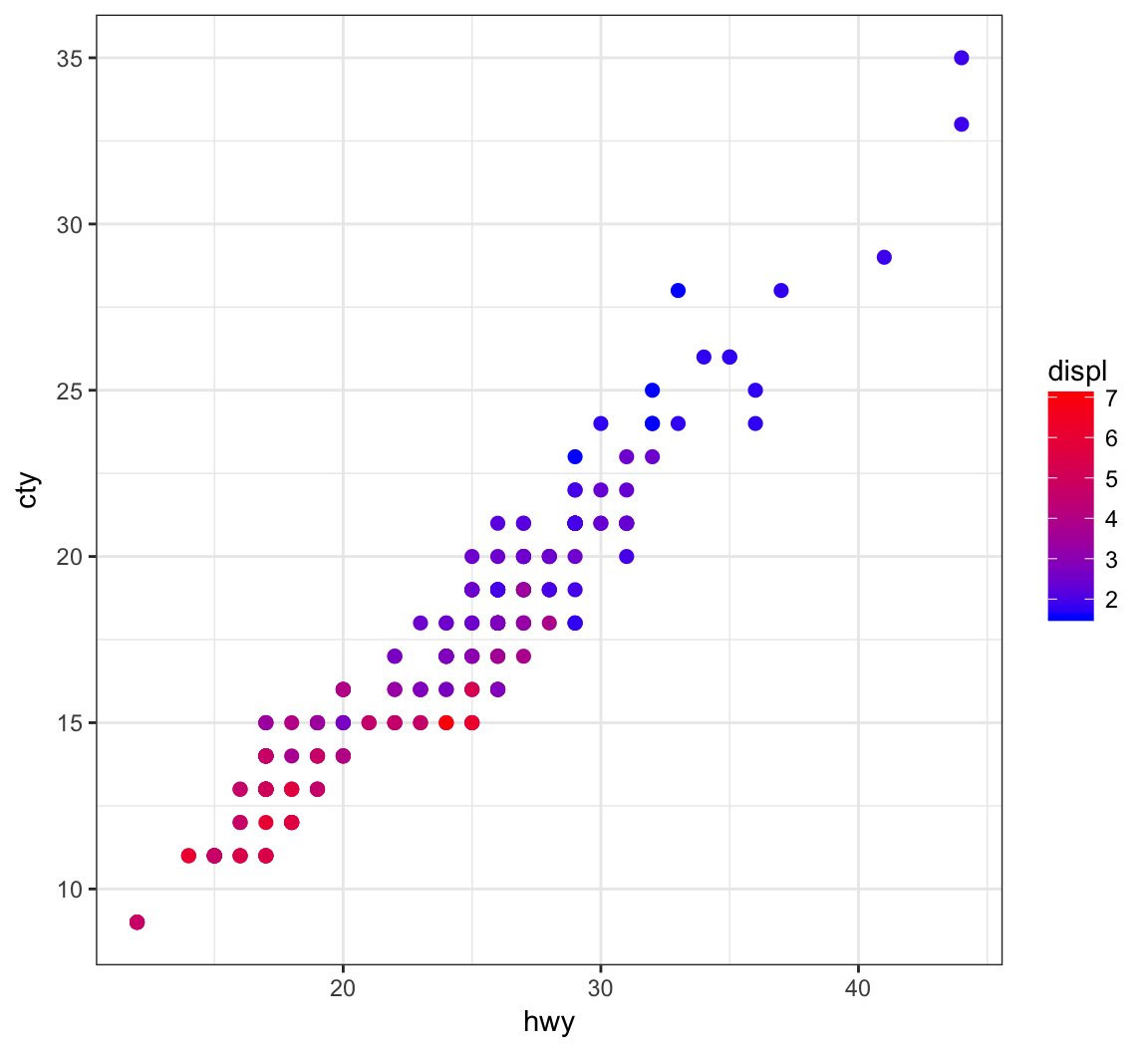
An example of using the palette “Set1” from the RColorBrewer package, included in ggplot2:
> ggplot(diamonds) +
+ geom_density(mapping = aes(x=price, color=clarity)) +
+ scale_color_brewer(palette = "Set1")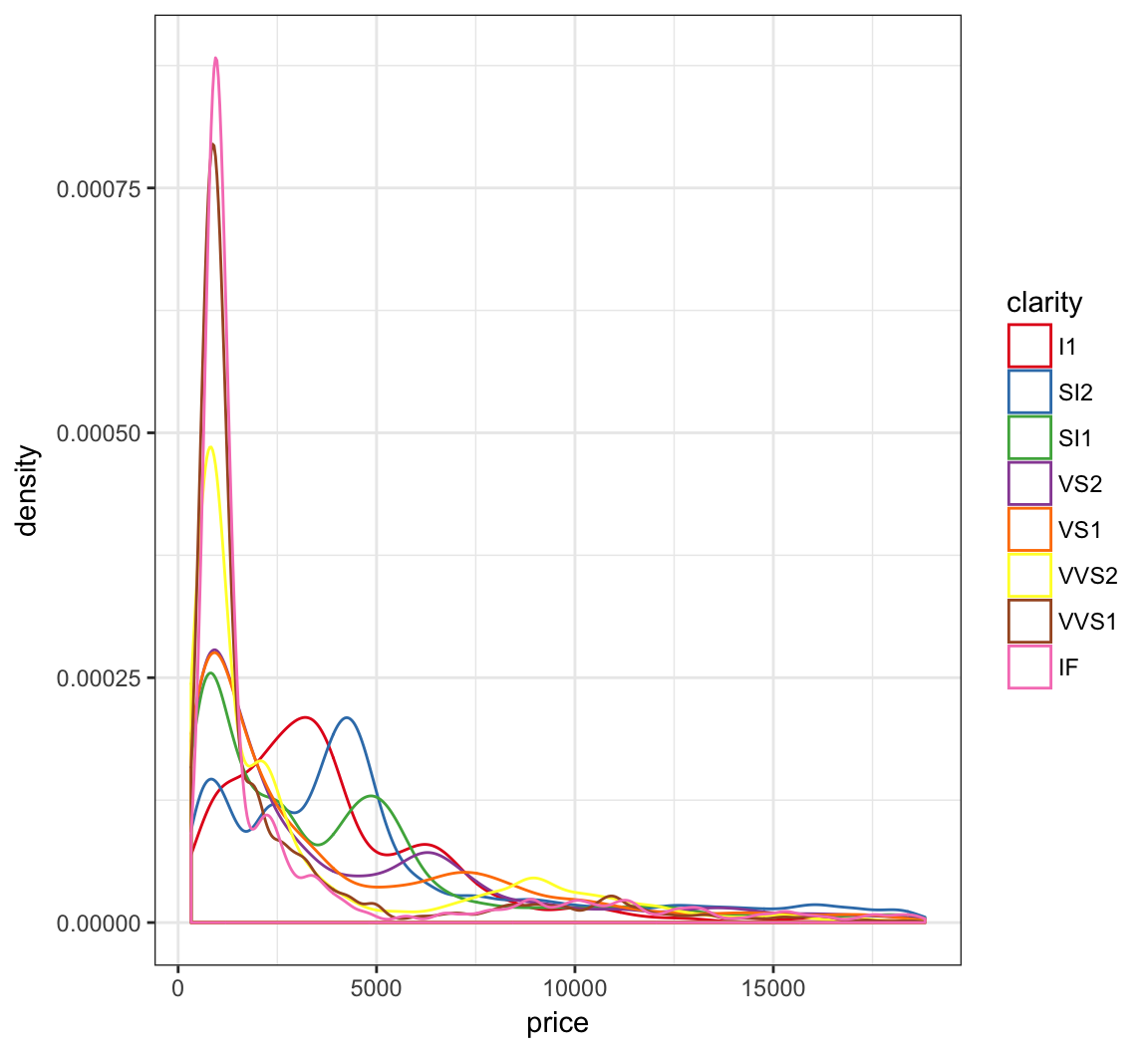
Another example of using the palette “Set1” from the RColorBrewer package, included in ggplot2:
> ggplot(data = mpg) +
+ geom_point(mapping = aes(x = displ, y = hwy, color = class)) +
+ scale_color_brewer(palette = "Set1")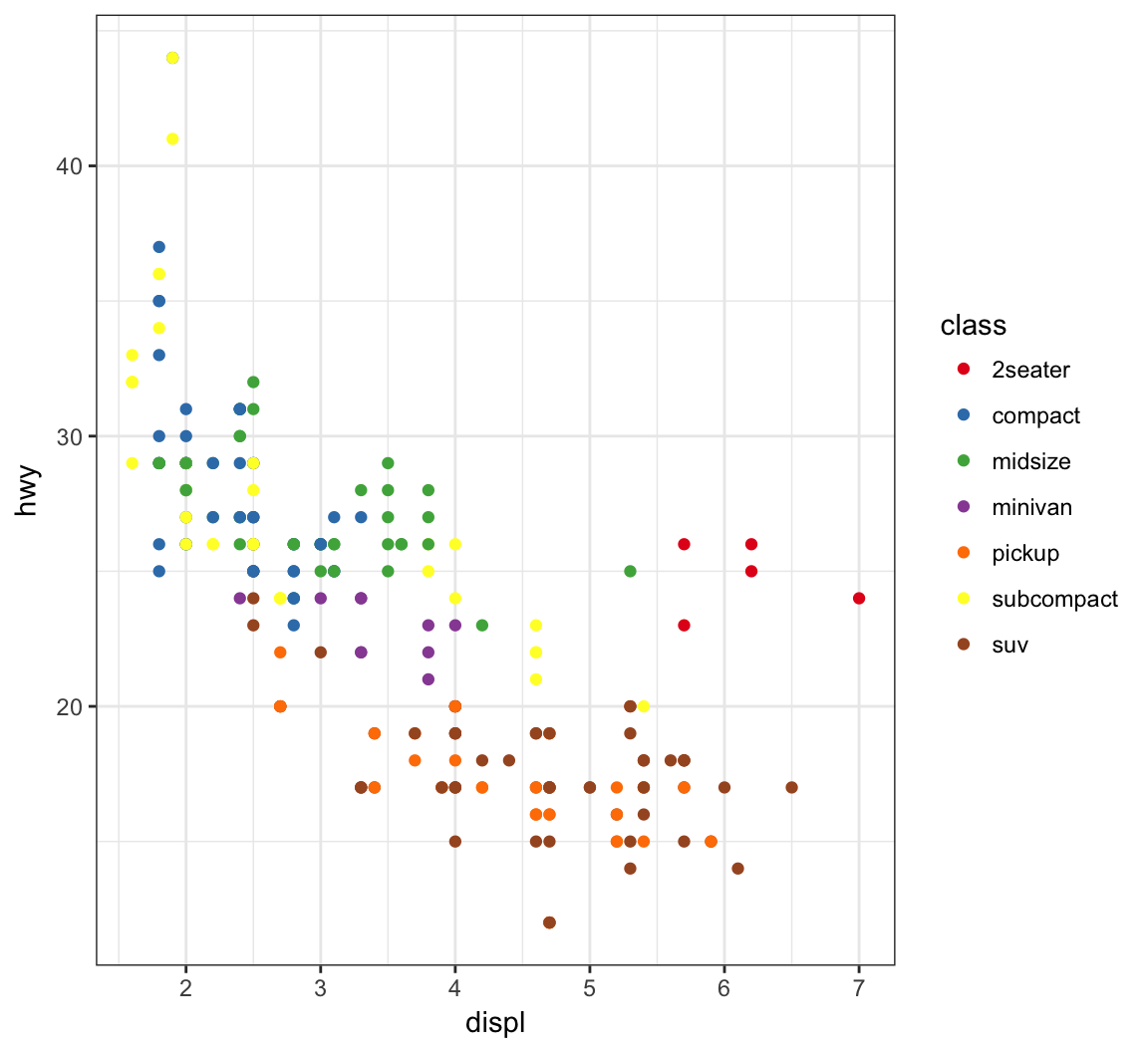
The gapminder package comes with its own set of colors, country_colors.
> ggplot(subset(gapminder, continent != "Oceania"),
+ aes(x = year, y = lifeExp, group = country,
+ color = country)) +
+ geom_line(show.legend = FALSE) + facet_wrap(~ continent) +
+ scale_color_manual(values = country_colors)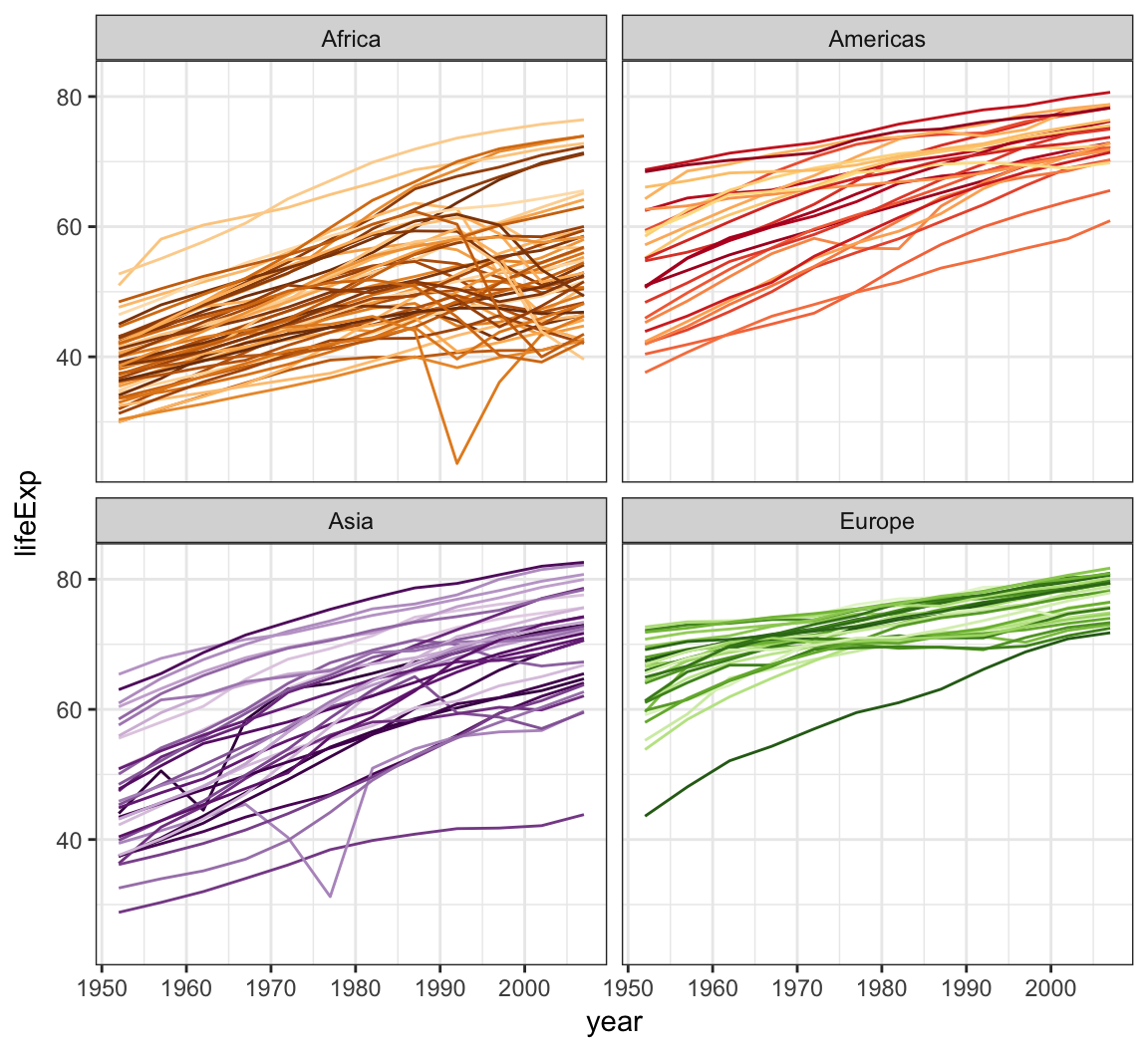
Saving Plots
Saving Plots as Variables
Pieces of the plots can be saved as variables, which is particular useful to explortatory data analysis. These all produce the same plot:
> ggplot(data = mpg, mapping = aes(x = displ, y = hwy, color=drv)) +
+ geom_point() +
+ geom_smooth(se=FALSE)> p <- ggplot(data = mpg, mapping = aes(x = displ, y = hwy, color=drv)) +
+ geom_point()
> p + geom_smooth(se=FALSE)> p <- ggplot(data = mpg, mapping = aes(x = displ, y = hwy, color=drv))
> p + geom_point() + geom_smooth(se=FALSE)Try it yourself!
Saving Plots to Files
Plots can be saved to many formats using the ggsave() function. Here are some examples:
> p <- ggplot(data = mpg, mapping = aes(x = displ, y = hwy, color=drv)) +
+ geom_point() +
+ geom_smooth(se=FALSE)
> ggsave(filename="my_plot.pdf", plot=p) # saves PDF file
> ggsave(filename="my_plot.png", plot=p) # saves PNG fileHere are the arguments that ggsave() takes:
> str(ggsave)
function (filename, plot = last_plot(), device = NULL,
path = NULL, scale = 1, width = NA, height = NA, units = c("in",
"cm", "mm"), dpi = 300, limitsize = TRUE, ...) Dynamic Visualization
Examples
Tools to dynamically interact with data visualizations (and calculations) are becoming increasingly common and straightforward to implement. Here are several examples:
> p <- ggplot(gapminder) +
+ geom_point(aes(x=gdpPercap, y=lifeExp, size = pop,
+ color = continent, frame = year)) +
+ scale_x_log10()
> gganimate(p, "animation_ex1.gif", ani.height=400, ani.width=500)The resulting file can be viewed here: https://github.com/jdstorey/asdslectures/blob/master/docs/images/animation_ex1.gif
> p <- ggplot(gapminder) +
+ geom_density(aes(x=lifeExp, color=as.factor(year),
+ frame=year),
+ size=1.2) +
+ scale_color_discrete(name="year")
> gganimate(p, "animation_ex2.gif", ani.height=400, ani.width=500)The resulting file can be viewed here: https://github.com/jdstorey/asdslectures/blob/master/docs/images/animation_ex2.gif
> p <- ggplot(gapminder) +
+ geom_density(aes(x=lifeExp, color=as.factor(year),
+ frame=year, cumulative = TRUE),
+ size=1.2) +
+ scale_color_discrete(name="year")
> gganimate(p, "animation_ex3.gif", ani.height=400, ani.width=500)The resulting file can be viewed here: https://github.com/jdstorey/asdslectures/blob/master/docs/images/animation_ex3.gif
Themes
Available Themes
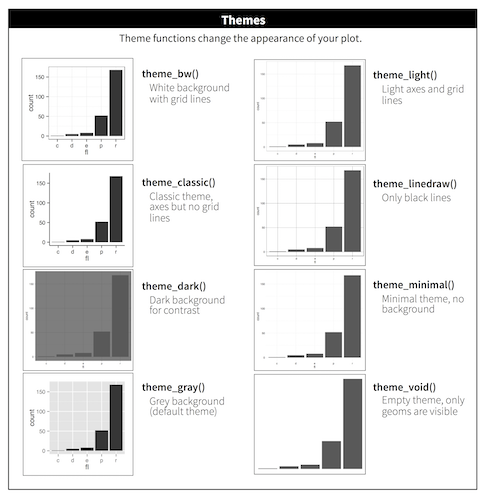
From http://r4ds.had.co.nz/visualize.html. See also ggthemes package.
Setting a Theme
Globally:
> theme_set(theme_minimal())Locally:
> ggplot(data = diamonds) +
+ geom_bar(mapping = aes(x = cut)) +
+ theme_minimal()More Numerical Summaries
Measuring Symmetry
The skewness statistic measures symmetry of the data. It is calculated by:
\[ \gamma = \frac{\sum_{i=1}^n (x_i - \overline{x})^3/n}{s^3} \]
A negative number is left-skewed, and a positive number is right-skewed.
Note: Use of \(n\) vs. \(n-1\) may vary – check the code.
skewness() Function
In R, there is a function call skewness() from the moments package for calculating this statistic on data.
> library(moments)
> gapminder %>% filter(year==2007) %>% select(gdpPercap) %>%
+ skewness()
gdpPercap
1.211228
> gapminder %>% filter(year==2007) %>% select(gdpPercap) %>%
+ log() %>% skewness()
gdpPercap
-0.1524203
> rnorm(10000) %>% skewness()
[1] -0.01402231Measuring Tails
The tails of a distribution are often described as being heavy or light depending on how slowly they descend.
This can be measured through statistic called kurtosis:
\[ \kappa = \frac{\sum_{i=1}^n (x_i - \overline{x})^4/n}{s^4} \] As with skewness \(\gamma\), use of \(n\) vs \(n-1\) may vary.
Excess Kurtosis
For a standard Normal distribution (mean 0 and standard deviation 1), the kurtosis is on average 3.
Therefore, a measure called “excess kurtosis” is defined to be \(\kappa - 3\). A positive value implies heavier tails and a negative value implies lighter tails.
kurtosis() Function
In R, there is a function call kurtosis() from the moments package for calculating this statistic on data.
> library(moments)
> gapminder %>% filter(year==2007) %>% select(gdpPercap) %>%
+ kurtosis()
gdpPercap
3.29593
> gapminder %>% filter(year==2007) %>% select(gdpPercap) %>%
+ log() %>% kurtosis()
gdpPercap
1.871608
> rnorm(10000) %>% kurtosis()
[1] 2.99372Visualizing Skewness and Kurtosis
Visualizing Skewness and Kurtosis
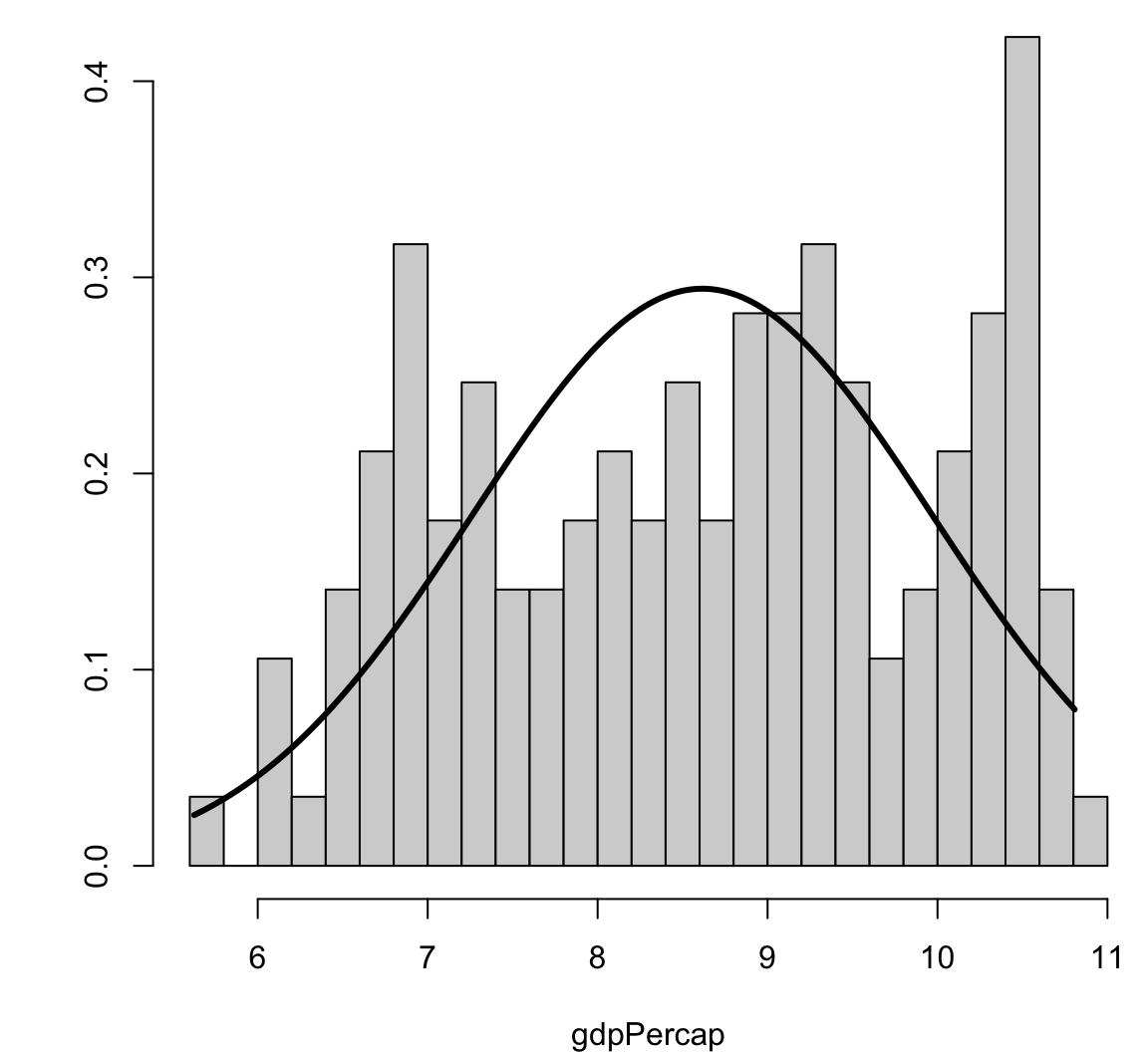
Correlation
It is often the case that two or more quantitative variables are measured on each unit of observation (such as an individual).
We are then often interested in characterizing how pairs of variables are associated or how they vary together.
A common measure that is used is called “correlation”, which is most well suited for measuring linear associations
Pearson Correlation
Suppose we observe \(n\) pairs of data \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\). Their sample correlation is
\[\begin{eqnarray} r_{xy} & = & \frac{\sum_{i=1}^n (x_i - \overline{x}) (y_i - \overline{y})}{\sqrt{\sum_{i=1}^n (x_i - \overline{x})^2 \sum_{i=1}^n (y_i - \overline{y})^2}} \\ \ & = & \frac{\sum_{i=1}^n (x_i - \overline{x}) (y_i - \overline{y})}{(n-1) s_x s_y} \end{eqnarray}\]where \(s_x\) and \(s_y\) are the sample standard deviations of each measured variable.
Spearman Correlation
There are other ways to measure correlation that are less reliant on linear trends in covariation and are also more robust to outliers.
Specifically, one can convert each measured variable to ranks by size (1 for the smallest, \(n\) for the largest) and then use a formula for correlation designed for these ranks.
One popular measure of rank-based correlation is the Spearman correlation.
> x <- rnorm(500)
> y <- x + rnorm(500)
> cor(x, y, method="pearson")
[1] 0.7542651
> cor(x, y, method="spearman")
[1] 0.7499555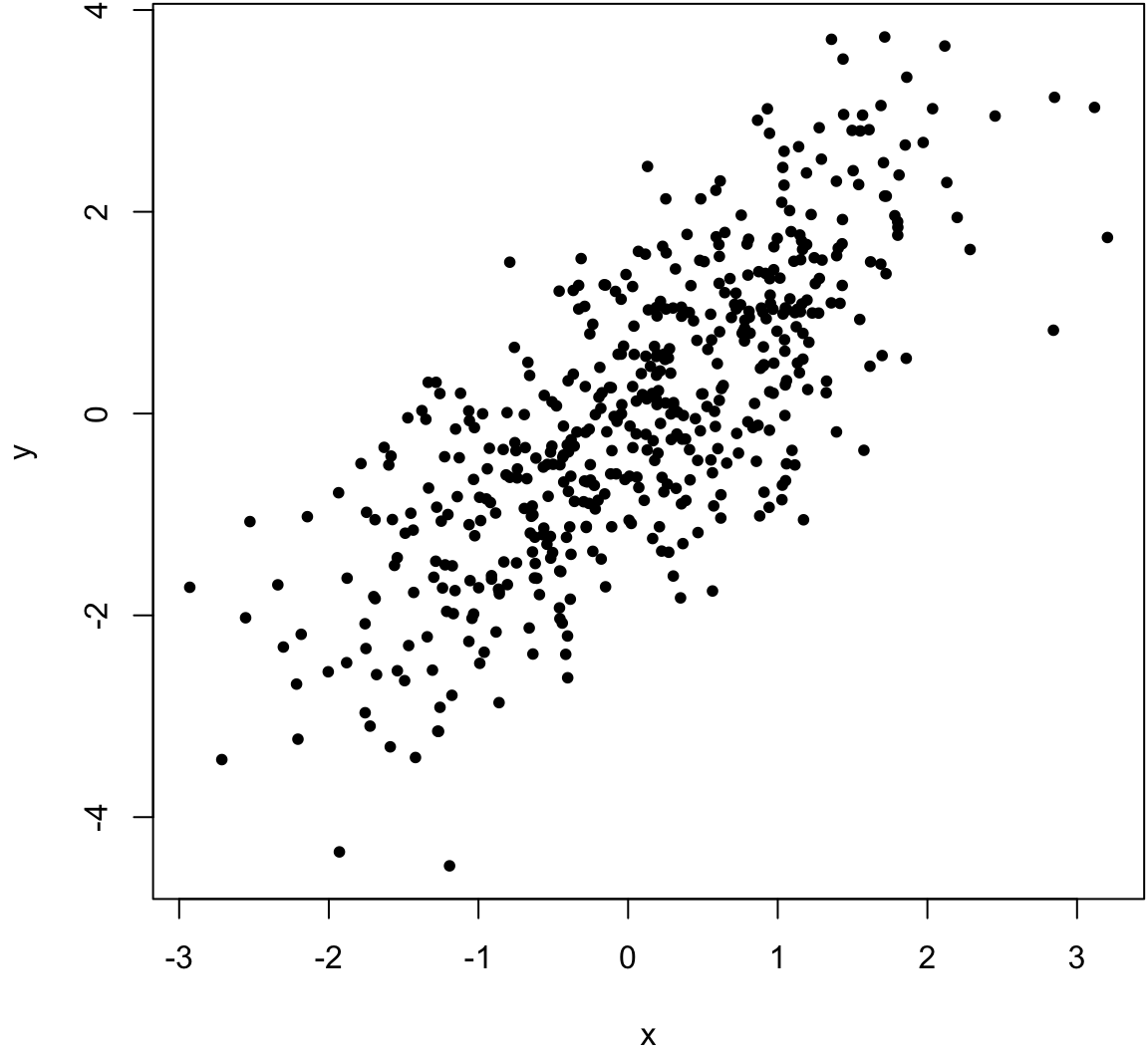
> x <- rnorm(500)
> y <- x + rnorm(500, sd=2)
> cor(x, y, method="pearson")
[1] 0.5164903
> cor(x, y, method="spearman")
[1] 0.5093092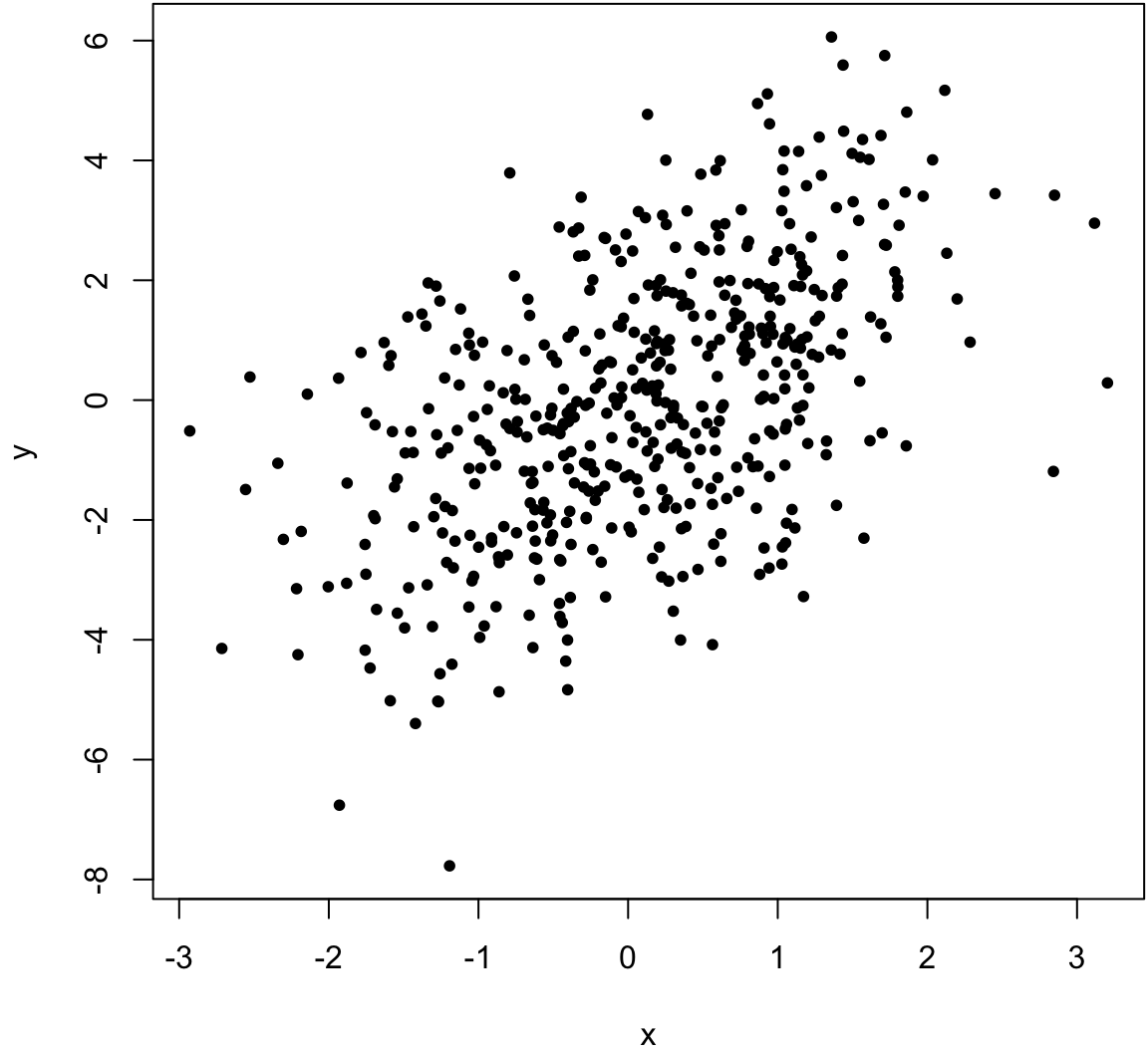
> x <- c(rnorm(499), 100)
> y <- c(rnorm(499), 100)
> cor(x, y, method="pearson")
[1] 0.9528564
> cor(x, y, method="spearman")
[1] -0.02133551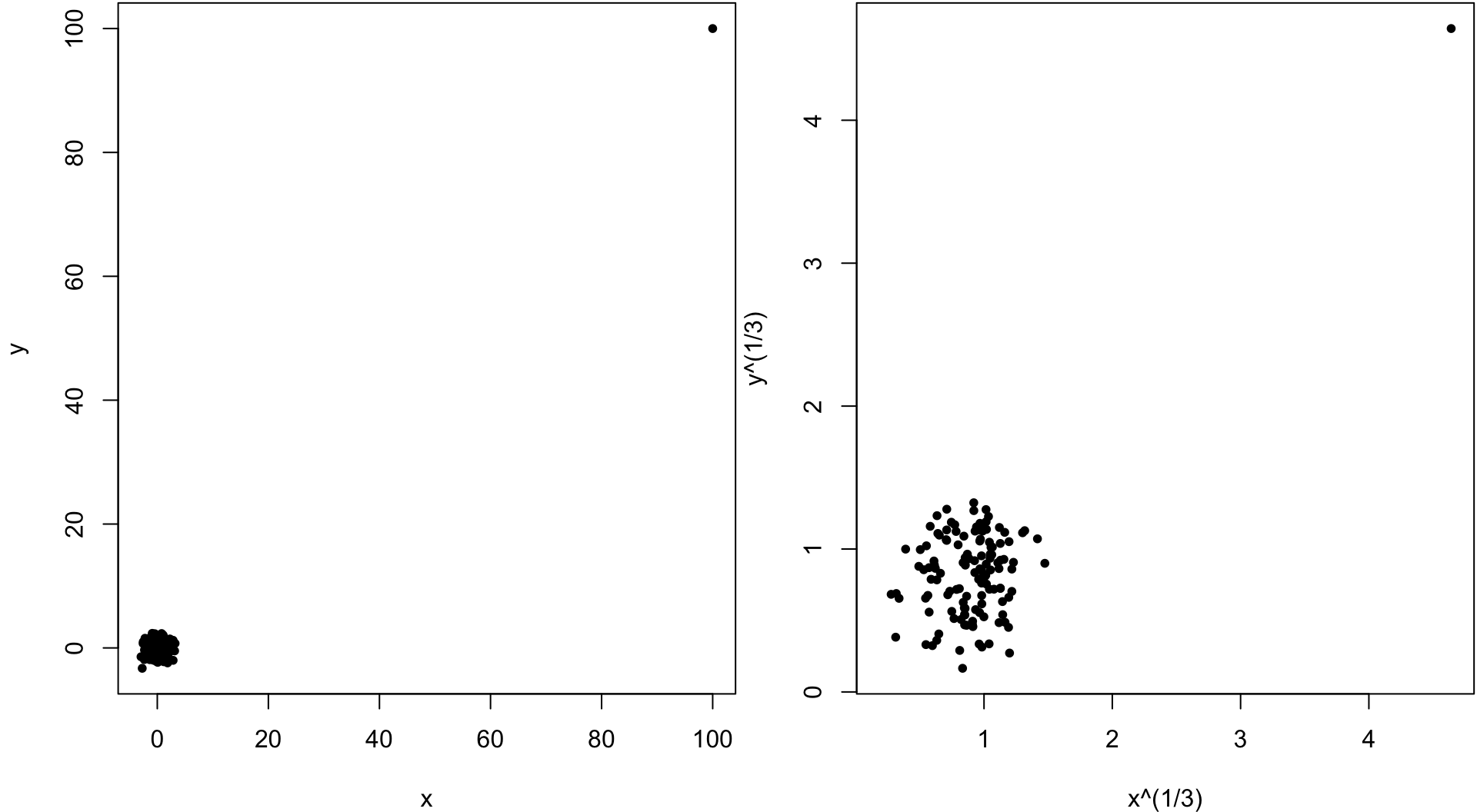
Quantile-Quantile Plots
Quantile-quantile plots display the quantiles of:
- two samples of data
- a sample of data vs a theoretical distribution
The first type allows one to assess how similar the distributions are of two samples of data.
The second allows one to assess how similar a sample of data is to a theoretical distribution (often Normal with mean 0 and standard deviation 1).
> qqnorm(mtcars$mpg, main=" ")
> qqline(mtcars$mpg) # line through Q1 and Q3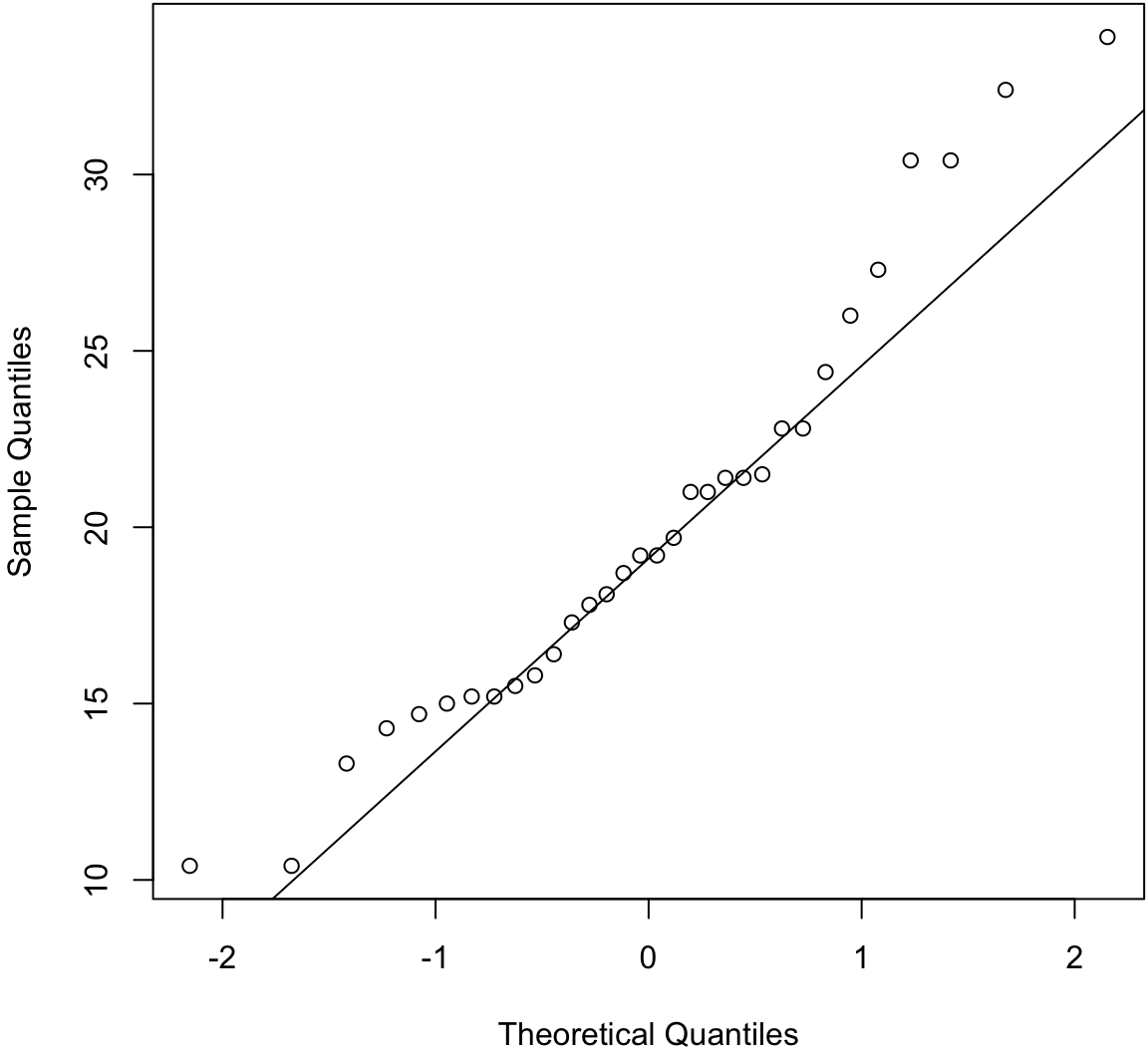
> before1980 <- gapminder %>% filter(year < 1980) %>%
+ select(lifeExp) %>% unlist()
> after1980 <- gapminder %>% filter(year > 1980) %>%
+ select(lifeExp) %>% unlist()
> qqplot(before1980, after1980); abline(0,1)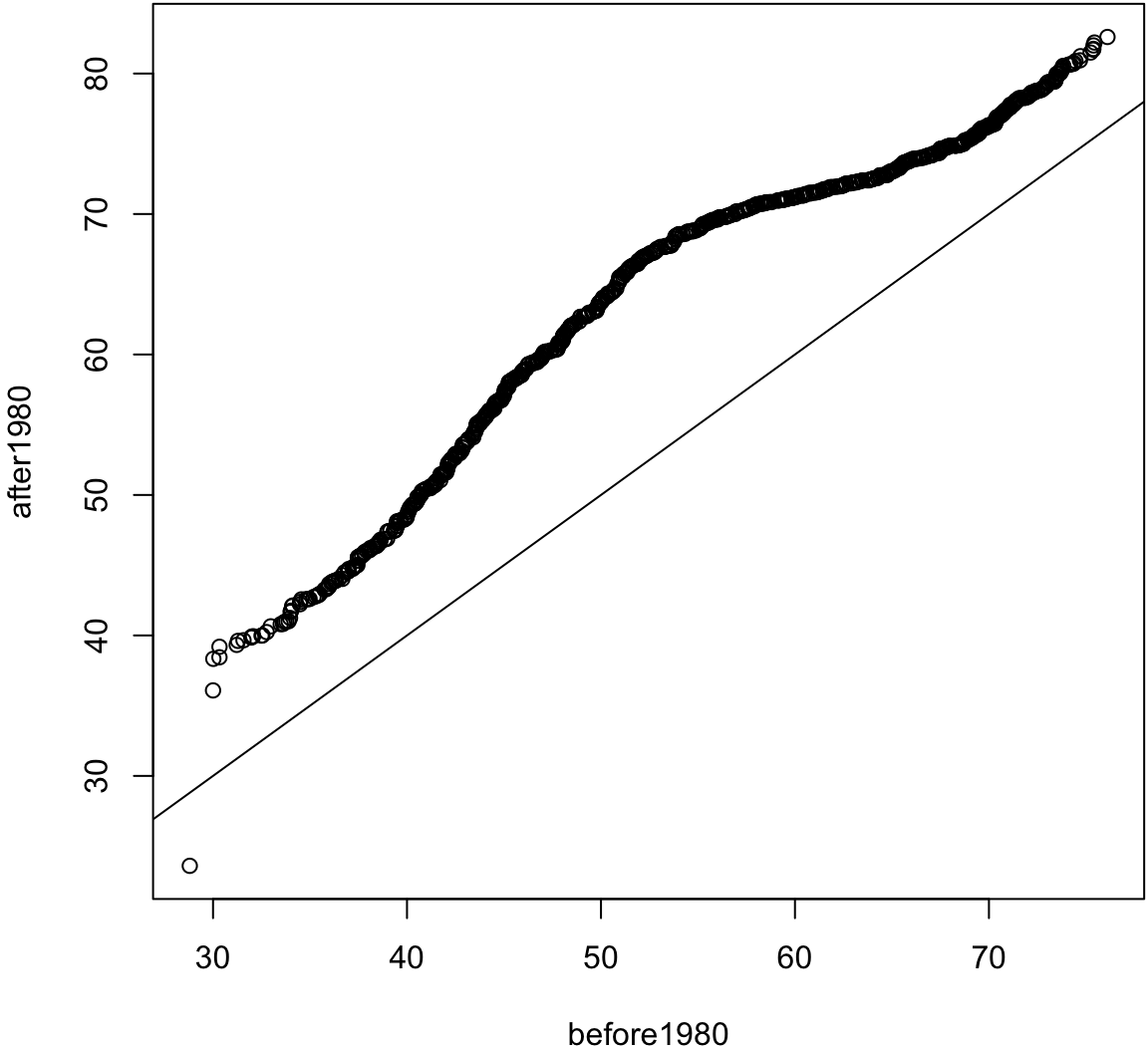
> ggplot(mtcars) + stat_qq(aes(sample = mpg))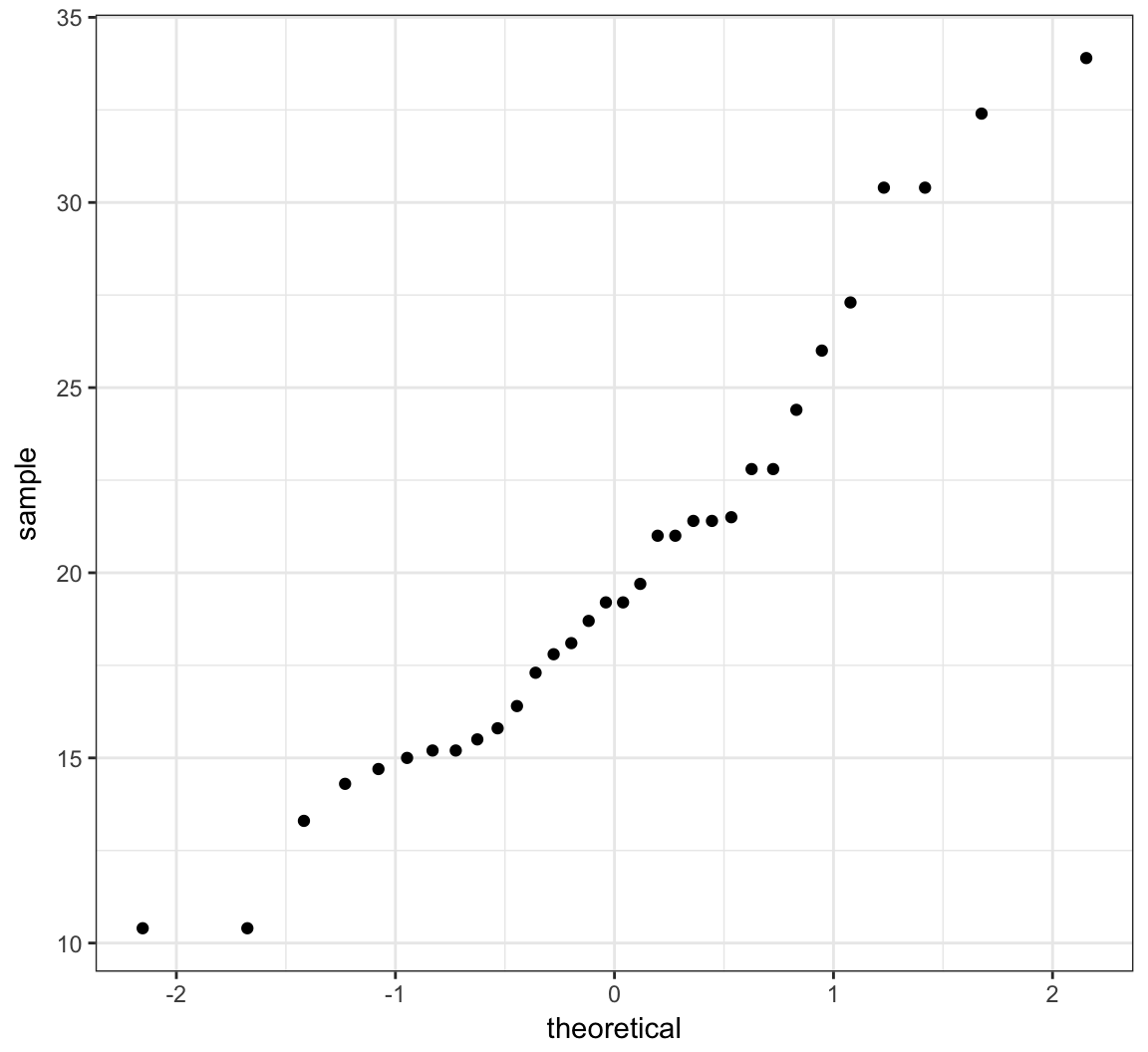
> ggplot(gapminder) + stat_qq(aes(sample=lifeExp))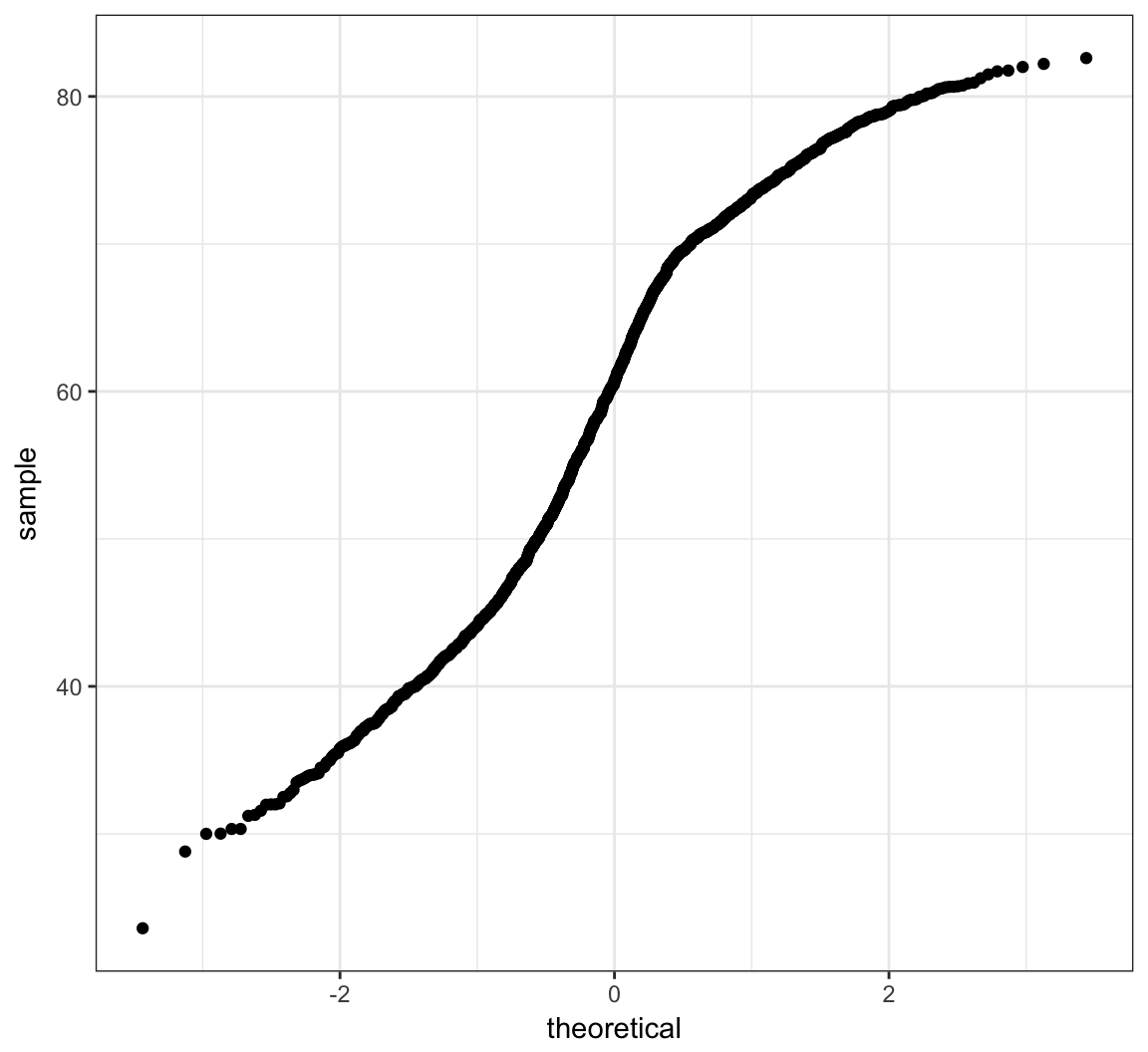
> ggplot(gapminder) +
+ stat_qq(aes(sample=lifeExp, color=continent))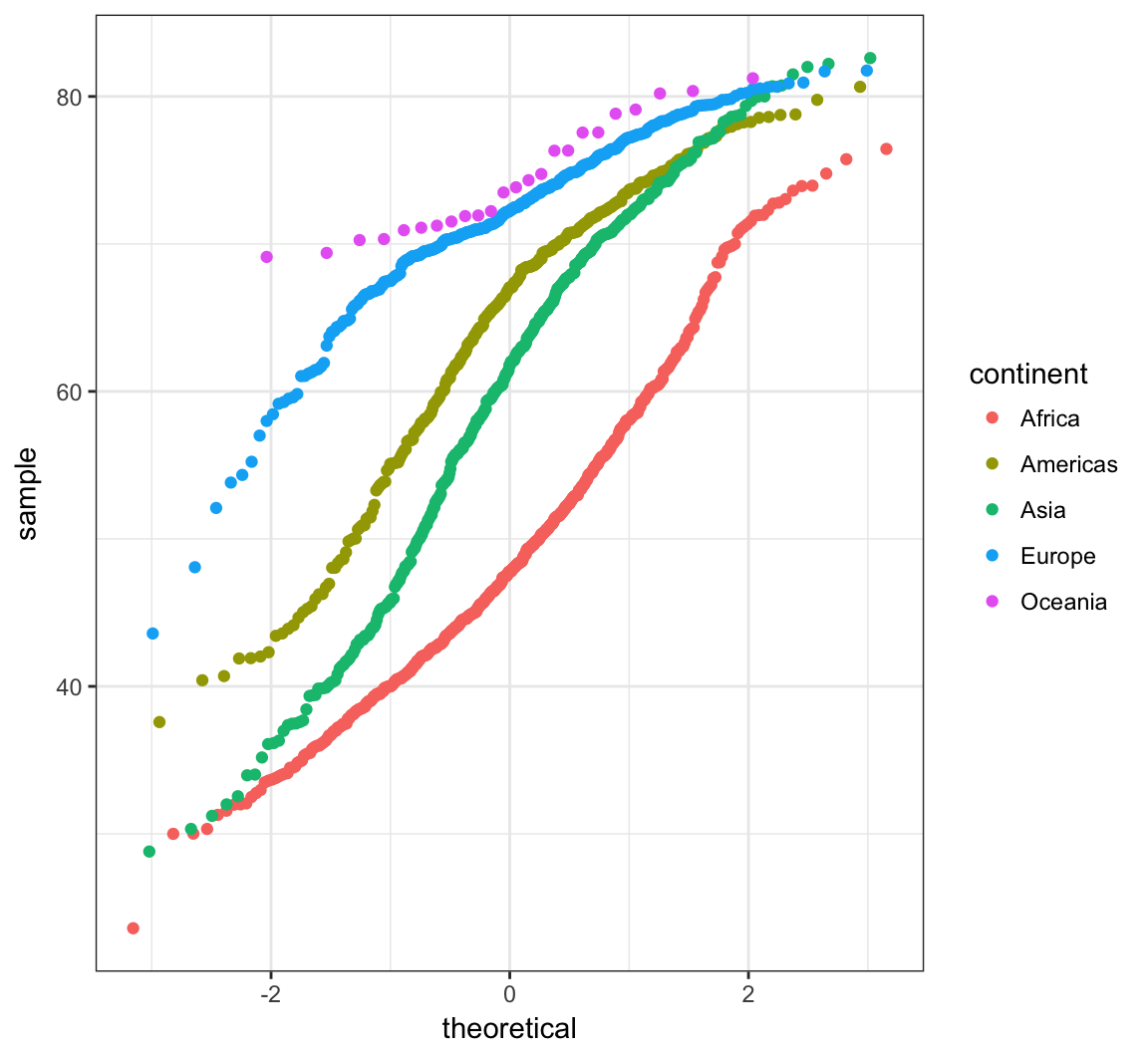
Extras
Source
Session Information
> sessionInfo()
R version 3.3.2 (2016-10-31)
Platform: x86_64-apple-darwin13.4.0 (64-bit)
Running under: macOS Sierra 10.12.4
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods
[7] base
other attached packages:
[1] moments_0.14 hexbin_1.27.1
[3] babynames_0.3.0 gapminder_0.2.0
[5] gganimate_0.1.0.9000 animation_2.5
[7] dplyr_0.5.0 purrr_0.2.2
[9] readr_1.1.0 tidyr_0.6.2
[11] tibble_1.3.0 ggplot2_2.2.1
[13] tidyverse_1.1.1 knitr_1.15.1
[15] magrittr_1.5 devtools_1.12.0
loaded via a namespace (and not attached):
[1] Rcpp_0.12.10 RColorBrewer_1.1-2 highr_0.6
[4] cellranger_1.1.0 plyr_1.8.4 forcats_0.2.0
[7] tools_3.3.2 digest_0.6.12 lubridate_1.6.0
[10] jsonlite_1.4 evaluate_0.10 memoise_1.1.0
[13] nlme_3.1-131 gtable_0.2.0 lattice_0.20-35
[16] psych_1.7.5 DBI_0.6-1 yaml_2.1.14
[19] parallel_3.3.2 haven_1.0.0 xml2_1.1.1
[22] withr_1.0.2 stringr_1.2.0 httr_1.2.1
[25] revealjs_0.9 hms_0.3 rprojroot_1.2
[28] grid_3.3.2 R6_2.2.0 readxl_1.0.0
[31] foreign_0.8-68 rmarkdown_1.5 modelr_0.1.0
[34] reshape2_1.4.2 backports_1.0.5 scales_0.4.1
[37] htmltools_0.3.6 rvest_0.3.2 assertthat_0.2.0
[40] mnormt_1.5-5 colorspace_1.3-2 labeling_0.3
[43] stringi_1.1.5 lazyeval_0.2.0 munsell_0.4.3
[46] broom_0.4.2